反应器-催化剂颗粒双尺度分析费托合成的产物分布及其影响因素

曹 军， 张 莉， 徐 宏

(华东理工大学 机械与动力工程学院， 上海 200237)

反应器-催化剂颗粒双尺度分析费托合成的产物分布及其影响因素

曹 军， 张 莉， 徐 宏

(华东理工大学 机械与动力工程学院， 上海 200237)

在考虑产物液膜传质阻力的情况下，构建了反应器-催化剂颗粒双尺度费托合成产物分布的多场耦合数学模型，讨论了产物液膜及催化剂粒径对产物分布特性的影响。结果表明，产物碳原子选择性的计算结果符合费托合成经典的ASF分布。反应物浓度在催化剂颗粒表面处的浓度最高，沿着半径方向向中心处不断降低，而产物的浓度分布状态则正好相反。沿着流动方向，主体气流中反应物CO的浓度要高于催化剂内部平均值，产物C5+浓度则与此相反；且浓度差异在反应器入口部分最为明显，随着反应不断进行，催化剂颗粒内外组分的浓度差异逐渐缩小。此外，催化剂粒径越大，颗粒内部组分的浓度差也越大，而减小粒径可以降低液态产物传质阻力，同时有效避免催化剂的“死区”现象，有利于提高其利用效率。

费托合成； 液膜传质系数； 扩散限制效应； 多尺度多物理场耦合分析

我国的能源分布具有“富煤、少气、贫油”的特点。中国石油经济技术研究院报告显示，2016年我国石油对外依存度达到62%[1]。将煤、天然气、生物质等含碳资源转化为合成气(CO和H2)之后，在催化剂及一定的反应条件下，利用费托合成反应(Fischer-Tropsch Synthesis)可将其进一步转化为液体燃料，在一定程度上实现对石油的替代，对保障我国能源供应安全具有重要意义[2-4]。依据目标产物及所采用的催化剂和反应条件的不同，费托合成一般分为高温费托合成[5]和低温费托合成[6]。前者的反应温度范围300～350℃，反应压力范围2.0～2.5 MPa，通常以Fe为催化剂；后者的反应温度范围200～250℃，压力范围2.0～5.0 MPa，通常以Co或者Fe为催化剂。另外，我国还自主开发并产业化了中温费托合成[7]，其反应温度范围为260～290℃。在几种典型的费托合成工艺中，高温费托合成产物主要为汽油、柴油、含氧有机化学品、烯烃等，在工业生产中被广泛应用。

现有对费托合成产物分布的研究大部分是在反应通道或者反应器尺度展开。实际上，催化剂颗粒尺度上的扩散传质过程对产物分布有重要影响[8]。由于催化剂本身的形状、尺寸以及内部孔隙分布状况(曲折因子)都会影响到反应组分在其中的内扩散，在催化剂颗粒尺度上考察反应组分在其中的传递及反应过程，有助于优化催化剂的设计，避免催化剂内部由于传递过程的限制而出现无法参与反应的“死区”。此外，费托合成产物种类众多，其中的一部分高沸点重质烃类产物往往以液体蜡的形式覆盖在催化剂颗粒表面并填充在催化剂颗粒的内部孔隙[9-10]，使得费托合成成为在气-液-固三相间溶解-扩散-反应耦合的复杂传质和反应过程，对反应速率和产物选择性产生重要影响。研究者提出了大量的模型来分析费托合成中的液相产物分布及气-液平衡，其中包括Raoult定律法[11]、K值法[12]、PR方程[13]、SRK方程[14]、基团贡献法[15]等。权桂英等[16]认为，对于理想性较强的烃类产物体系(如高温低压体系)或C18以下的轻质烃类，体系的气-液平衡可采用Raoult定律描述，C18以上的重质烃类由PR 方程计算则更为合适。王逸凝等[17]则用状态方程关联了多组分气相主体在催化剂孔道中与蜡的溶解平衡，同时探讨了在被蜡填充的催化剂颗粒的孔道中的主要反应行为，初步考察了颗粒内扩散-反应在不同操作温度和压力下的匹配规律。李永旺[18-19]等也关注费托合成气-液平衡问题，并通过修正的SRK方程，分析了单颗粒中费托合成组分的分布情况。

笔者通过构建包含有动量、质量传递以及费托合成反应动力学方程的多物理场耦合数值模型，在考虑液态产物扩散传质阻力的条件下，在反应器和单个催化剂颗粒两个尺度上，分析了管式固定床反应器中高温费托合成产物无量纲浓度分布特性及其影响因素，并提出了减小液膜传质阻力的方法。相关模型和结论有助于进一步理解费托合成反应中的传递过程，并对催化剂的设计有一定的指导意义。

1 用于分析费托合成产物分布的双尺度多场耦合数学模型的建立与求解

1.1 数学模型的建立

建立如图1所示的三维数值模型。假设管式反应器长度为Lb，半径为Rb，其中填充有半径为rp的球形Fe-HZSM-5催化剂颗粒，床层孔隙率为εb，渗透率为κ。为了得到在反应器及单个催化剂颗粒上的费托合成反应物及产物的浓度分布特性，需要构建在两个尺度上相互耦合的包含有动量、质量传递以及化学反应的多物理场数值模型。在进行模型构建时，进行以下3点假设。

图1 计算中所用的反应器-催化剂颗粒双尺度耦合数学模型Fig.1 Reactor-catalyst particle double-scale coupledmodel used in the simulation

(1)整个催化剂填充床层为均匀的多孔介质结构。

(2)催化剂颗粒为粒径一致的内部具有多孔结构的圆球。根据实际工业费托合成过程，认为反应过程中催化剂表面覆盖着一层液态蜡膜，且颗粒内部被液态蜡完全填充，液态产物对于组分的扩散产生传质阻力。

(3)管式反应器与外部冷却工质有良好的传热能力，高温费托合成反应在等温条件下进行。

1.2 费托合成的动力学方程

费托合成的产物分布非常复杂，研究者也得出了多个不同的费托合成产物的预测模型。当以Fe-HZSM-5 为催化剂，温度和压力分别位于290～310℃(563～583 K)以及1.5～2.3 MPa，n(H2)/n(CO)在0.76～1.82范围时，费托合成过程中的主要反应如式(1)～(8)所示[20]，反应的动力学方程如式(9)所示。

CO+3H2→CH4+H2O

(1)

2CO+4H2→C2H4+2H2O

(2)

2CO+5H2→C2H6+2H2O

(3)

3CO+7H2→C3H8+3H2O

(4)

4CO+9H2→n-C4H10+4H2O

(5)

4CO+9H2→i-C4H10+4H2O

(6)

6.05CO+12.23H2→C6.05H12.36(C5+)+6.05H2O

(7)

CO+H2O↔CO2+H2(水汽变换反应)

(8)

(9)

式(9)中，Ri为化学反应速率，mol/(kgcat·s)；pCO和pH2分别为反应气体CO和H2的分压，Pa；T为反应温度，K；R为摩尔气体常数，J/(mol·K)；相应于反应(1)～(8)的反应动力学参数m、n、ki以及活化能(Ei)的值列于表1。

对于反应式(1)～(8)中所示的2种反应物的消耗速率和9种不同的产物的生成速率可分别由式(10)～(20)表示。

RCO=-ρcat(R1+2R2+2R3+3R4+4R5+4R6+6.05R7+R8) (10)

RC2H6=ρcatR3

(14)

RC3H8=ρcatR4

(15)

Rn-C4H10=ρcatR5

(16)

Ri-C4H10=ρcatR6

(17)

RC5+=ρcatR7

(18)

RCO2=ρcatR8

(19)

RH2O=ρcat(R1+2R2+2R3+3R4+
4R5+4R6+6.05R7-R8)

(20)

式(10)～(20)中，ρcat表示催化剂的密度，kg/m3。

1.3 控制方程

基于上述假设及反应动力学方程，费托合成过程中的主要控制方程如式(21)～(23)所示。

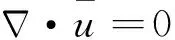
(21)

(22)

(23)

(24)

Ni,inward=hD,i(Ci-Cp,i)

(25)

式(24)、 (25)中，xi为各个组分的摩尔分数；Mi为各个组分的相对分子质量；p为反应压力，Pa；T为反应温度，K，R为摩尔气体常数，J/(mol·K)；Cp,i为催化剂颗粒内部的组分浓度，mol/m3；hD,i为组分在催化剂颗粒表面液膜中的传质系数，表征液膜对气相反应物传质过程的影响，可用式(26)计算。

(26)

式(26)中，Dl表示组分在液膜中的扩散系数，m2/s；rp为催化剂颗粒半径，m；Sh为定义为对流传质与扩散传质之比的舍伍德数(Sherwood number)，可由Frossling关系式(27)计算。

Sh=2+0.552Re1/2Sc1/3

(27)

式(27)中，Re表示雷诺数；Sc表示施密特数；分别由式(28)、(29)计算。

(28)

(29)

对于球型催化剂颗粒，式(23)中的Sp可以由式(30)计算。

(30)

1.4 边界条件

对于发生费托合成反应的管式固定床反应器模型，其入口、出口、管壁和圆管轴线边界条件可表示为式(31)～(34)。

(1)入口(z=0,0

u=uin，v=0，CCO=CCO,in，CH2=CH2,in

(31)

(2)出口(z=Lb,0

(32)

(3)管壁(r=Rb，0≤z≤Lb)

(33)

(4)圆管轴线(r=0，0≤z≤Lb)

(34)

1.5 反应器结构及工况计算参数与模型求解

在模型求解过程中，如无特别说明，用到的反应器尺寸及其它主要计算参数如表2所示。利用有限元方法建立数学模型并对其开展计算分析，所有计算结果均经过了网格无关性验证，所示结论均为反应达到稳定状态之后的计算结果。模型验证已有论述[21]，此处不再赘述。

表2 双尺度费托合成数值模型中用到的计算参数Table 2 Parameters used in the double scale Fischer-Trospch synthesis simulation model

2 结果与讨论

2.1 反应器尺度上的组分浓度分布特性及产物选择性

采用表2设定的计算参数，反应达到稳定状态之后，沿着反应通道轴线的反应物CO和H2转化率示于图2。由图2可以看到，在入口区域，由于反应物浓度高，消耗速率较大，反应物转化率迅速上升；随着反应的不断进行，反应物浓度及消耗速率逐渐降低，因此沿着气体流动方向的CO和H2转化率上升幅度也有所放缓；到反应通道出口处时，H2已经基本完全参与反应，CO的转化率接近80%。从计算可知，设定工况下6m的反应管长即可实现对于合成气的转化，计算结果与Rahimpour 等[20]的结论相似。该结论对于工业生产中反应器的设计有一定的指导意义。

图2 沿反应器床层轴线上反应物CO及H2的转化率(Xi)Fig.2 The conversion rates(Xi) of CO and H2 reactantsalong the reaction tube axisReaction conditions： uin=0.1 m/s, CCO,in=210 mol/m3,CH2,in=210 mol/m3, n(CO)/n(H2)=1

以烃类产物的碳原子选择性(SC,n)来表征费托合成各个烃类产物的相对量，如式(35)所示。

(35)

式(35)中，Cn为反应器出口处碳原子数为n的烃类产物的浓度，mol/m3；CCO,in，CCO,out以及CCO2,out分别为反应器进口处、出口处的CO浓度以及出口处的CO2浓度，mol/m3。

同时，为了便于将产物选择性计算结果与经典的ASF分布相比较，将集总反应动力学方程中的C2H4与C2H6合并，将n-C4H10与i-C4H10合并，从而得到C1、C2、C3、C4以及C5+产物在反应器出口处的碳原子选择性，如图3所示。由图3可以看到， C2的选择性比C1低，C3有所上升，C4又进一步减少，符合ASF分布规律。所有烃类产物中，C5+产物的碳原子选择性最高，达到27.9%，而CH4的选择性也达到了24%。因此，进一步优化反应条件及催化剂性能，减少CH4的选择性仍然是需要进一步研究的课题。

图3 本模型计算得到的费托合成烃类产物的碳原子选择性Fig.3 The C-atom selectivity of Fischer-Tropsch synthesis hydrocarbon products obtained from the developed modelReaction conditions： uin=0.1 m/s, CCO,in=210 mol/m3,CH2,in=210 mol/m3, n(CO)/n(H2)=1

2.2 催化剂颗粒尺度上的组分浓度分布特性

反应组分在催化剂颗粒中的浓度分布对于催化剂的设计具有重要意义。图4(a)、(b)是与图3相同的反应工况下，反应通道中心轴线上距离入口1 m 位置处的催化剂颗粒中反应物CO以及代表性产物C5+的3D无量纲浓度分布云图，图4(c)则为同一个催化剂颗粒中沿着半径方向的CO及C5+的无量纲浓度分布曲线(分别以CCO_nondim及CC5+_nondim表示)。由图4可以看到，对于反应物CO，催化剂颗粒表面处的浓度最高，沿着半径方向向中心处不断降低，在1 mm的半径长度内，无量纲浓度从表面处的1下降到中心的0.81，下降趋势明显；产物C5+的浓度分布则正好相反，最高浓度出现在催化剂颗粒中心处，外表面浓度最低。这是由于床层主体气流中的CO在经过扩散穿过催化剂颗粒表面覆盖的液膜之后，首先到达其外表面，然后再开始在填充有液态产物的颗粒内部孔道中的内扩散与反应过程。由于内扩散的限制，加上反应的不断进行，使得能够到达催化剂中心位置的CO浓度不断下降。在催化剂的设计中，粒径过大容易存在反应物无法到达的“死区”，造成催化剂的浪费，因此要根据反应物在颗粒中的扩散特性进行粒径的优化设计。对于产物C5+，其传质过程则正好相反，在催化剂颗粒中生成之后，需要经由内扩散及外扩散过程到达床层主体气流；由于越靠近中心位置处的产物越难以扩散出去，因此浓度分布是由内而外逐渐降低。二次反应与烯烃再吸附理论[21]指出，催化剂孔道内液相产物的存在减缓了烯烃的脱除，导致其溶解度和停留时间增加，进而在催化剂活性位上再吸附的可能性增大，并发生二次链增长反应，从而使得费托合成产物偏离ASF分布。因此，催化剂粒径对于产物的选择性有重要影响。

2.3 液膜对产物分布特性的影响

由于催化剂表面液膜的传质阻力，加上组分在颗粒中参与反应，使得反应物及产物在床层主体气流以及催化剂颗粒中的浓度分布呈现差异。图5(a)为沿着反应通道轴线方向，反应器主体气流以及催化剂颗粒内部平均的CO和产物C5+的无量纲浓度分布。可以看到，沿着流动方向，主体气流中CO的浓度要高于催化剂内部平均值，且这种差异在入口部分最为明显，随着反应不断进行，差异逐渐缩小，到出口处基本趋于一致。这是由于入口段反应物浓度高，CO的消耗速率大，而液态产物对CO的扩散限制效应使催化剂中消耗的CO不能从外部得到及时的补充，从而使颗粒中的浓度较之主体气流有较大的差异；随着反应不断进行，CO浓度减小，催化剂中的反应消耗速率也有所减小，尽管扩散限制仍然存在，但是此时从外部扩散补充进来的CO逐渐可以满足反应的消耗，因此催化剂内部和外部主体气流中的CO浓度逐渐趋于一致。产物C5+分布规律与反应物CO正好相反，C5+在催化剂内部的浓度要高于主体气流，且随着反应的不断进行，浓度差异也不断减小，最终趋于一致。这是由于一开始产物的生成速率较大，受液膜的扩散限制，催化剂颗粒内部的C5+产物无法完全扩散到主体气流，随着反应不断进行，生成速率逐渐降低，最终逐渐达到了内部生成与向外扩散的动态平衡。

图4 单个催化剂颗粒内部CO及C5+无量纲浓度分布Fig.4 The non-dimensional concentration distributions of CO and C5+ inside catalyst particle(a) Non-dimensional concentration distribution contour of CO; (b) Non-dimensional concentration distribution contour of C5+;(c) Non-dimensional concentration distribution along particle radiusReaction conditions： uin=0.1 m/s, CCO,in=210 mol/m3, CH2, in=210 mol/m3, n(CO)/n(H2)=1

图5 反应器轴线上主体气流及催化剂颗粒内部平均的CO和C5+无量纲浓度分布Fig.5 The non-dimensional concentration of CO and C5+in the main flow and average value inside catalyst particle(a) CO; (b) C5+Reaction conditions： uin=0.1 m/s, CCO,in=210 mol/m3, CH2,in=210 mol/m3, n(CO)/n(H2)=1

2.4 催化剂粒径对产物分布特性的影响

从式(26)可得，液膜对于传质过程的影响主要是通过液膜传质系数hD,i表征，而结合式(27)、(28)以及式(29)可得式(36)。

(36)

由式(36)可见，主体气流流速u、催化剂颗粒的半径rp、组分在液膜中的扩散系数D，以及液膜本身的密度ρ和黏度μ均会影响到液膜传质系数hD,i，进而对组分在反应中的内、外扩散过程产生影响。在催化剂设计层面，催化剂颗粒半径rp成为决定液膜传质系数hD,i的主要因素。图6(a)所示为反应工况如表2所示条件下，当催化剂半径分别为0.5、1.0、2.0 mm时，沿着反应管轴线方向，主体气流中以及催化剂颗粒内部平均的反应物CO及产物C5+的无量纲浓度分布。可以看到，当催化剂粒径为0.5 mm时，颗粒内CO平均浓度与主体气流中的浓度差异几乎可以忽略，而当催化剂粒径增大到2.0 mm时，入口位置处催化剂颗粒内部的平均浓度只有主体气流的65.9%。说明CO不能及时扩散进入催化剂颗粒内部，且催化剂粒径越大，其中与主体气流浓度的差异越大。随着反应的不断进行，沿着气体流动方向，不同粒径催化剂之间的浓度平均值差距逐渐减小。以上现象的出现与液态产物的扩散限制效应密切相关。由式(36)可知，增大催化剂粒径会减小液膜传质系数hD,i，造成CO向颗粒内部扩散的阻力增大，从而造成催化剂内、外的更为明显的浓度差异。随着反应的不断进行，主体气流中CO浓度下降，CO消耗速率降低，催化剂内部逐渐达到了CO的反应消耗与扩散补充的平衡，此时催化剂粒径增大所造成的扩散限制效应逐渐变弱，因此不同粒径催化剂内部的CO浓度分布逐渐趋于一致。

图6(b)为与图6(a)相同的反应工况下，位于反应管轴线上距离入口1 m位置处不同粒径催化剂中的CO无量纲浓度分布。由图6(b)可见，当粒径为0.5 mm时，催化剂表面的CO浓度与中心位置只有大约4.2%的差异；当粒径增大为2 mm时，表面与中心位置的浓度差达到78.1%。也即粒径越大，催化剂颗粒内部的反应物浓度分布越不均匀，这不利于活性组分的均匀利用，容易造成颗粒外层催化剂已经失活而中心位置处催化剂仍然活性高的状况，从而造成活性组分的浪费。

图7所示为同一操作工况下，主体气流与不同粒径催化剂颗粒中产物C5+的平均浓度对比。在反应器同一位置处，催化剂粒径越大，其内部平均的C5+浓度就越高，同时与主体气流中的C5+浓度差异也越大。这同样是由于较大的催化剂粒径造成较低的液膜传质系数的较大的传质阻力，限制了C5+产物向主体气流的扩散，从而造成颗粒内部更高的C5+浓度。与反应物CO相同的是，沿着反应通道，随着反应不断进行，3种不同粒径催化剂中的C5+浓度也逐渐趋于一致。这同样是因为当反应不断进行时，C5+生成速率下降，由于粒径不同造成的扩散能力差异对其向外扩散传质的限制效应逐渐减弱，因此不同粒径催化剂内部平均的C5+产物浓度差异也逐渐减小，最终与主体气流中的浓度趋于一致。

图6 不用粒径时反应器轴线上催化剂颗粒内部平均组分无量纲浓度分布Fig.6 The component non-dimensional average concentrations inside catalyst particle along the reactor axis at different particle radii(a) CO; (b) C5+Reaction conditions： uin=0.1 m/s, CCO,in=210 mol/m3, CH2,in=210 mol/m3, n(CO)/n(H2)=1

图7 不用粒径时反应器轴线上催化剂颗粒内部C5+组分无量纲浓度分布Fig.7 The component non-dimensional average concentrationsinside catalyst particle along the reactor axis at different particle radii Reaction conditions： uin=0.1 m/s, CCO,in=210 mol/m3,CH2, in=210 mol/m3, n(CO)/n(H2)=1

基于以上结论可以看出，在实际生产中，减小催化剂粒径是降低液态产物传质阻力的一种有效方法。较小粒径的催化剂可以降低由于反应物向内以及产物向外扩散的阻力，同时，较小粒径的催化剂也使反应能在整个颗粒中均匀的进行，避免了大粒径催化剂只能利用到壳层一小部分活性组分，造成内部活性组分浪费的“死区”现象，有利于提高催化剂的利用效率。然而，同时也要看到，催化剂颗粒较小时，反应器内催化剂床层气体阻力会较大，不利于原料气进料与空速的加大，因此在选择催化剂颗粒粒径时，要注意传质效率与床层阻力之间的平衡，选取合适的粒径，粒径并非越小越好。

3 结 论

(1)在费托合成反应中，反应物在催化剂颗粒表面处的浓度最高，沿着半径方向向中心处不断降低，而产物的浓度分布则正好相反。较大的催化剂粒径容易造成颗粒内的反应“死区”，同时导致产物溶解度和停留时间增加，并发生二次链增长反应。

(2) 在费托合成反应中，反应器内沿着流动方向，主体气流中CO的浓度要高于催化剂内部平均值，且这种差异在入口部分最为明显；随着反应不断进行，从外部扩散补充进来的CO逐渐可以满足反应的消耗，催化剂颗粒内外的浓度差异逐渐缩小。产物C5+的浓度分布规律则与此相反。

(3) 减小催化剂粒径是降低液态产物传质阻力的一种有效方法。较小粒径的催化剂可以降低由于反应物向内以及产物向外扩散的阻力，同时，也使反应能在整个颗粒中均匀进行，避免了催化剂颗粒内的“死区”现象，有利于提高催化剂的利用效率；然而，较小的粒径也会增大床层中的气体流动阻力，因此在粒径的选择上要考虑传质效率和阻力之间的平衡。

[1] 2015年国内外油气行业发展报告[R].中国石油经济技术研究院， 2016. (Gas and Oil Industry Development Report at Home and Abroad of 2015[R]. China Petroleum Economics & Technology Research Institute, 2016.)

[2] WOOD D A, NWAOHA C, TOWER B F. Gas to liquids(GTL): A review of an industry offering several routes for monetizing natural gas[J].Journal of Natural Gas Science and Engineering, 2012, 9: 196-208.

[3] DAVIS B H. Fischer-Tropsch synthesis: Overview of reactors development and future potentials[J].Topics in Catalysis, 2005, 32: 143-168.

[4] 孙启文. 煤炭间接液化[M].北京： 化学工业出版社， 2012.

[5] 陈振涛， 徐春明.重质油在孔道内扩散传质的研究进展[J].化工学报， 2016, 67(1): 165-175. (CHEN Zhentao, XU Chunming. Progress of research on diffusional transport of heavy oil in pores[J]. CIESE Journal, 2016, 67(1): 165-175.)

[6] BASSEEM B H, KEYVANLOO K, HEDENGRENJD. An optimized simulation model for iron-based Fischer-Tropsch catalyst design: Transfer limitations as functions of operating and design conditions[J].Chemical Engineering Journal, 2015, 263(1): 268-279.

[7] 相宏伟, 杨勇， 李永旺. 煤炭间接液化: 从基础到工业化[J].中国科学: 化学, 2014, 44(12): 1876-1892. (XIANG Hongwei, YANG Yong, LI Yongwang. Indirect coal-to-liquids technology from fundamental research to commercialization[J].Scientia Sinica Chimica, 2014, 44(12): 1876-1892.)

[8] BHATELIA T, LI C, SUN Y. Chain length dependent olefin re-adsorption model for Fischer-Tropsch synthesis over Co-Al2O3catalyst[J].Fuel Processing Technology, 2014, 125: 277-289.

[9] MASUKUA C M, MA W, HILDEBRANDTB D, et al.A vapor-liquid equilibrium thermodynamic model for a Fischer-Tropsch reactor[J].Fluid Phase Equilibria, 2012, 314: 38-45.

[10] VISCONTI C G, MASCELLARO M. Calculating the product yields and the vapor-liquid equilibrium in the low-temperature Fischer-Tropsch synthesis[J].Catalysis Today, 2013, 214: 61-73.

[11] CALDWELL L, VAN VUUREN D S. On the formation and composition of the liquid phase in Fischer-Tropsch reactors[J].Chem Eng Sci, 1986, 41(1): 89-96.

[12] MARANO J J, HOLDER G D. Characterization of Fischer-Tropsch liquids for vapor-liquid equilibria calculations[J].Fluid Phase Equilib, 1997, 138(1): 1-21.

[13] VISCONTI C G. Vapor-liquid equilibria in the low-temperature Fischer-Tropsch synthesis[J].Ind Eng Chem Res, 2014, 53(5): 1727-1734.

[14] TSONOPOULOS C, HEIDMAN J L. High-pressure vapor-liquid equilibria with cubic equations of state[J].Fluid Phase Equilib, 1986, 29: 391-414.

[15] CHEN Z, YAO Z, LI Y, et al. Prediction of vapor-liquid equilibrium at high pressure using a new excess free energy mixing rule coupled with the original UNIFAC method and the SRK equation of state[J].Ind Eng Chem Res, 2009, 48(14): 6836-6845.

[16] 权桂英， 唐晓津， 张占柱. 费托合成反应体系的气液平衡研究进展[J].过程工程学报， 2014， 14(6): 1063-1071. (QUAN Guiying, TANG Xiaojin, ZHANG Zhanzhu. Research progress in vapor-liquid equilibrium of Fischer-Tropsch synthesis system[J].The Chinese Journal of Process Engineering, 2014, 14(6): 1063-1071. )

[17] 王逸凝, 李永旺, 赵玉龙, 等. 固定床费托(FT)合成单颗粒催化剂模拟[J].化学反应工程与工艺, 2000, 12(6): 109-115. (WANG Yining, LI Yongwang, ZHAO Yulong, et al. Modeling of catalyst pellet for fixed-bed Fischer Tropsch synthesis[J].Chemical Reaction Engineering and Technology, 2000, 12(6): 109-115.)

[18] XU J, YANG Y, LI YW. Fischer-Tropsch synthesis process development: Steps from fundamentals to industrial practices[J].Current Opinion in Chemical Engineering, 2013, 2: 354-362.

[19] LIU Z Y, SHI S D, LI Y W. Coal liquefaction technologies-development in China and challenges in chemical reaction engineering[J].Chem Eng Sci, 2010, 65: 12-17.

[20] RAHIMPOUR M R, MIRVAKILI A, PAYMOONI K, et al. A comparative study between a fluidized-bed and a fixed-bed water perm-selective membrane reactor with in situ H2O removal for Fischer-Tropsch synthesis of GTL technology[J].Journal of Natural Gas Science and Engineering, 2011, 3: 484-495.

[21] TAU L M, DABBAGH A, DAVIS B H. Fischer-Tropsch synthesis: 14C tracer study of alkene incorporation[J]. Energy Fuels, 1990, 4: 94-99.

[22] 曹军， 张莉， 徐宏. 管式固定床反应器中Fe基费托合成的多物理场耦合数值分析[J].石油学报(石油加工)， 2016, 32(6): 79-84. (CAO Jun, ZHANG Li, XU Hong. Multiphysics-coupled numerical analysis on Fe-based Fischer-Tropsch synthesis in tubular fixed-bed reactor[J]. Acta Petrolei Sinica (Petroleum Processing Section)， 2016, 32(6): 79-84.)

The Analysis on Products Distribution and Influence Factors ofFischer-Tropsch Synthesis by Reactor-Catalyst Particle Double-Scale

CAO Jun， ZHANG Li， XU Hong

(SchoolofMechanicalandPowerEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

A multi-scale and multi-physics-coupled numerical model containing the momentum, mass transfer, as well as the chemical Fischer-Tropsch synthesis kinetic equations in both reactor and catalyst particle scales with the consideration of mass transfer resistance caused by liquid products film on catalyst particle surface, was established. The effects of liquid film as well as the particle radius on products distribution characteristics were analyzed. The results showed that the C-atom selectivity of Fischer-Tropsch products obtained from the established numerical model agreed well with the classical ASF distribution. The highest reactant concentration appeared at the out surface of catalyst particle and decreased along the particle radius, while there was an opposite trend for product concentration. The CO concentration in main flow was higher than the average value in catalyst particle, while the product C5+has the opposite distribution character. Moreover, the concentration difference between main flow and catalyst particle was largest at the inlet region, and decreased along the flow direction. Furthermore, the larger the catalyst particle, the more obvious the concentration difference along the particle radius of the components inside the particle. Thus smaller catalyst particle is good for decreasing the diffusion limitation, to avoid the “dead region” phenomenon, and the catalyst usage efficiency can also be enhanced.

Fischer-Tropsch synthesis; liquid film mass transfer coefficient; diffusion limitation effect; multi-scale multi-physics coupled analysis

2016-04-18

中央高校基本科研业务费探索基金项目(WG1414044)资助

曹军，男，助理研究员，主要从事石油化工多场耦合数值仿真的研究工作；Tel:021-64253810；E-mail:caojun@ecust.edu.cn

徐宏，男，教授，主要从事过程强化的研究工作；Tel:021-64253810；E-mail:hxu@ecust.edu.cn

1001-8719(2017)02-0252-09

TE65

A

10.3969/j.issn.1001-8719.2017.02.009