两版高中数学教材的比较研究——以“解三角形”为例

西南大学数学与统计学院(400715) 肖皓月

两版高中数学教材的比较研究
——以“解三角形”为例

西南大学数学与统计学院(400715) 肖皓月

一、问题的提出

教材是学生学习,教师教学的重要工具.新课程改革开始以来,在《普通高中数学课程标准(实验)》的指导下,我国高中数学教材相继出现了六个版本,打破了“一纲一本”的局面,实现了“一标多本”.随着教材编写的多样化,不同教材之间的比较研究也受到了前所未有的关注.

本研究选用的人民教育出版社出版的普通高中课程标准实验教科书数学A版(以下简称“人教A版”)及湖南教育出版社出版的普通高中课程标准实验教科书数学(以下简称“湘教版”),在现行教材中运用范围较广,且在国内以及国际上受到广泛关注.三角形是最基本的几何图形,三角形的数量关系是最基本的数量关系[1].解三角形就是探讨三角形中的数量关系,它是高中数学重要内容之一,其所蕴含的数学思想在现实生活中有着极其广泛的应用.本研究使用Seán Delaney(2007)在研究塞浦路斯、爱尔兰、台湾三地区教材中建立的水平和垂直的二维框架[2],对“人教A版”和“湘教版”两版数学教材进行比较研究,研究两版教材对于“解三角形”这章的内容呈现方式有何异同,对学生的期望又是什么?

二、研究设计

(一)研究对象

本文的研究对象分别是人教A版必修5和湘教版必修4高中数学教材中“解三角形”这章内容.具体内容如表1:

表1

(二)研究框架及编码

1 研究框架

本研究借鉴的是Seán Delaney(2007)在研究塞浦路斯、爱尔兰、台湾三地区教材中分数加减法内容建立的水平和垂直的二维框架[2].具体选取的指标如表2:

表2

2 编码

3 指标的度量

3.1 水平维度指标的度量

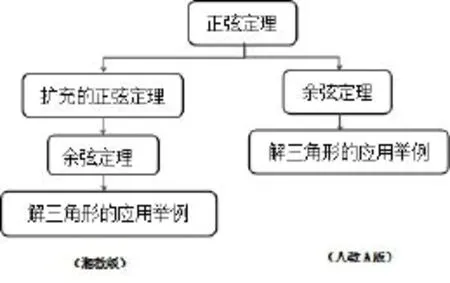
图1 主要内容及顺序的统计

3.2 垂直维度的度量

垂直维度中范例、概念结构、认知要求、作答类型等相关指标的具体量化将在下文“研究结果”中一一给出.

三、研究结果及分析

(一)水平维度的比较

由图1可以看出人教A版和湘教版的主要内容有细微差别,主要内容的呈现方式大致相同.湘教版相比于人教版A版多了扩充的正弦定理这部分内容,且这部分内容也是高考重点,虽人教A版未呈现,但大部分使用人教A版教材的课堂,教师需对这部分内容进行补充.相比之下,湘教版呈现的内容更为完整,更方便教师的使用.

表3

(二)垂直维度的比较

1.范例的比较

表4

由表4可知,两版教材范例数量大致相同,给出方法都只有一种,且都是给出了完整的解题步骤.两版教材都未更多的给出学生学习解三角形的机会.

2.概念结构的比较(针对任务)

表5

由表5可知,人教A版(66个)任务数量高于湘教版(49个).两版教材都有超过40%的任务都是关于三角形基本元素的计算,且都有超过30%的任务是关于解三角形实际应用.但是人教A版还有18%的任务是关于用正余弦定理相关问题的证明,而湘教版没有涉及这部分的任务.另外湘教版有少部分任务涉及三角形外接圆面积的计算,而人教版这部分任务没有.

3.认知要求的比较

图2

观察图2可以发现,两版教材对学生都有较高的认知要求,其中人教版高水平认知要求(联系型程序、做数学)占93%,湘教版占89%,人教A版对学生认知要求略高于湘教版.

4.作答类型的比较

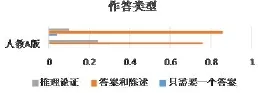
图3

如图3,两版教材超过70%部分任务都需要学生给出答案和陈述,其中湘教版高于人教A版;其次两版教材只需学生给出一个答案的任务很少,湘教版不足10%,人教版为零;再者人教A版需要学生推理论证的任务明显高于湘教版.

四、研究结论

(一)教材的呈现方式

通过分析比较,两版教材呈现的主要内容顺序大致相同,都是先学习正弦定理和余弦定理的基础上再来将其运用于现实情境中解决实际问题,但相对于人教版,湘教版呈现的主要内容更为完整.它将扩充的正弦定理也呈现在教材上,更好的方便教师的教学.但主要内容的呈现顺序对学生的学习质量影响较小,概念的结构以及范例的多样性才能决定学生真正学到什么[]3.两版教材从针对任务的概念结构来看涉及方面都比较多,从范例来看,两版教材都给出了完整步骤,但所有范例都只采用了一种方法,给学生提供的学习机会都较少.解决问题方法的多样化有助于学生数学思维的发展,笔者认为若两版教材若能在范例解题方法上给出更多解法,将更有助于学生对本章内容进行多角度有效的学习.

(二)教材对学生的期望

从认知要求来看,两版教材对学生的期望都较高,涉及高水平的认知要求两版教材都在90%左右;而且从作答类型来看,都有超过70%的任务要求学生给出答案和陈述.但其中人教A版作答类型中只需学生给出一个答案的任务没有,需学生给出推理论证的任务明显高于湘教版,笔者认为人教A版对学生的期望略高于湘教版.两版教材大部分任务都要求学生给出答案和陈述,但推理论证这方面涉及都太少,笔者认为任务应以答案和陈述为主,但也应适当增加推理论证方面的任务,以保证学生多方面能力全面发展.

[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.

[2]Seán Delaney,CY Charalambous,H Hsu,V Mesa(2007).The treatment of addition and subtraction of fractions in Cypriot,Irish and Taiwanese textbooks.PME CONFERENCE.

[3]袁思情,陈月兰.一篇值得推荐的数学教材分析框架文章[J].数学教学,2011,(04):21-24