一道立体几何题的思考

佛山市实验中学(528061) 谢伟帆

一道立体几何题的思考

佛山市实验中学(528061) 谢伟帆

1 试题呈现

2 试题分析

图1

3 渐入误区

由于割补法可以使问题简单化,学生在思考的时候第一个想法是将四面体补成四棱柱,球的直径为四棱柱的对角线长,如图2所示.

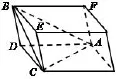
图2

4 错因分析

总结:外接球问题可以补成棱柱必须满足两个条件:(1)底面对角互补(2)侧棱垂直底面.结合本题,若∠BDC=120°,则可补成四棱柱.

5 正解发现

此题的正确解法是怎样呢?经过思考,学生提出了自己的想法.

法一:学生A提出用向量的方法解决,因为AD⊥面BCD,这样给建立空间直角坐标系提供了方便,这种方法固然可行,但运算量较大.

法二:学生B是这样考虑的,∠ADC=90°,取AC中点为F,则点F到点A,D,C的距离相等.如图3,作面ADC的垂线FG,由勾股定理知点G到点A,D,C的距离相等,只需使BG=AG,则G为外接球球心.

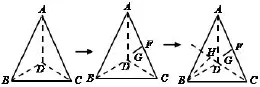
图3

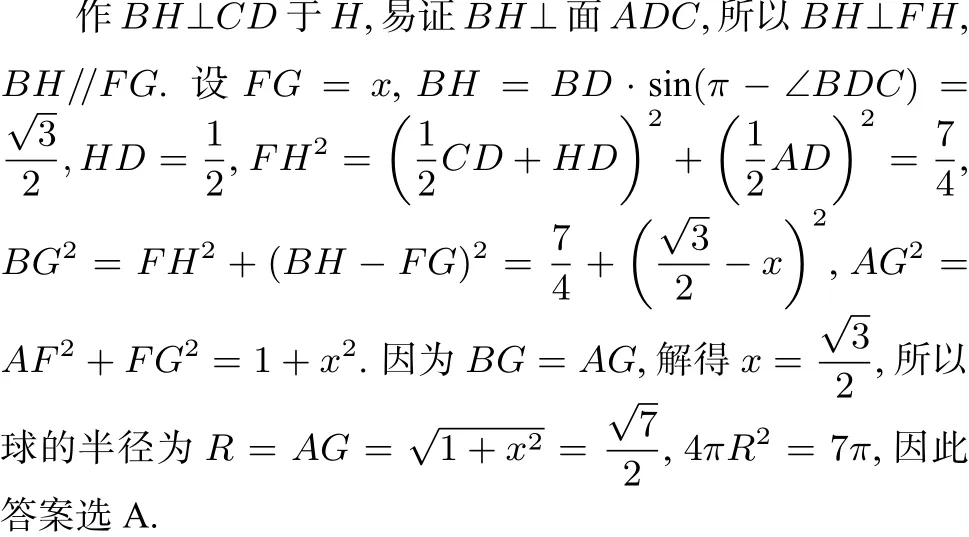
总结:法二利用直角三角形找出到三个顶点距离相等的点F,通过面的垂线,使得到第四个点的距离与之前的距离相等,从而确定球心和半径.此方法要求有较强的空间想象能力及运算能力.

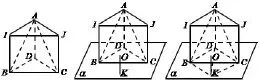
图4

结合学生B的想法,O是球心,K∈α,OK⊥α,所以K到B,D,C的距离相等.因为BD=CD=1,∠BDC=120°,因此K恰好是以BD,CD为邻边的平

总结:法三利用了直三棱柱外接球的性质:球心到底面的距离等于侧棱的一半,结合了法二,直接计算出球的半径.此法非常巧妙,融合了割补法、代数的思想,是数形结合思想很好的体现.

6 总结反思

利用了几何性质往往能更直观地揭示隐藏的关系,使得运算简便,这是纯代数方法所不具备的,也是数形结合妙处所在.