利用曲线的切线解题

广东省中山纪念中学(528454) 李文东

利用曲线的切线解题

广东省中山纪念中学(528454) 李文东

切线是曲线割线的极限位置,它反映了曲线的局部的几何性质.如果我们能够利用曲线的切线与曲线的几何位置关系,则能为我们的解题带来极大的方便,本文举例加以说明,展示切线的作用.

一、利用切线构造函数不等式

我们知道：若f(x)在区间[a,b]上为凸函数,则f(x)在区间[a,b]上任意一点处的切线位于函数f(x)图像的上方(除切点外);若f(x)在区间[a,b]上为凹函数,则f(x)在区间[a,b]上任意一点处的切线位于函数f(x)图像的下方(除切点外).

例1.考虑函数y=ex在x=0处的切线：y=x+1,结合函数y=ex为凹函数可得不等式：ex≥x+1,当且仅当x=0时取等号;进而可得ln(x+1)≤x,当且仅当x=0时取等号.又如考虑函数y=xlnx在x=1处的切线：y=x-1,结合函数y=lnx为凹函数可得不等式：xlnx≥x-1,即≤lnx,当且仅当x=1时取等号;从而有≤ln(x+1),当且仅当x=0时取等号.于是可得经典不等式：≤ln(x+1)≤x,当且仅当x=0时取等号.

又如函数y=sinx和函数y=tanx在x=0处的切线：y=x;在区间上,函数y=sinx为凸函数,函数y=tanx为凹函数,故有不等式：若,则 sinx＜x＜tanx.

二、利用切线证明不等式

例2.已知a+b+c=1,求证：.

例3.(2013全国卷)设函数f(x)=ex-ln(x+m),当m≤2时,证明f(x)＞0.

证明函数y=ex在x=1处的切线方程为y=x+1,从而有ex≥x+1,等号当且仅当x=0时成立;而函数y=ln(x+m)在x=1-m处的切线方程为y=x+m-1,函数y=ln(x+m)为凸函数,从而ln(x+m)≤x+m-1,等号当且仅当x=1-m时成立;因为m ≤ 2,故ln(x+m)≤x+m-1≤x+1≤ex,等号不同时成立,从而ln(x+m)＜ex.

三、利用切线讨论函数零点个数问题

例4.已知函数f(x)=x2-alnx(a∈R),讨论方程f(x)=0解的个数,并说明理由.

解方程 f(x)=x2-alnx=0的解的个数 ⇐⇒x2=alnx的解的个数 ⇐⇒函数y=x2与函数y=alnx的图像交点的个数.设函数y=x2与函数y=alnx在点P(x0,y0)处有相同的切线(公切线),则,从而a=e.作出函数y=x2与函数y=elnx的图像如图所示,它们在点处相切.由此可见：当a∈[0,e)时,函数y=x2与函数y=alnx的图像无交点,方程f(x)=0无解;当a＜0或a=e时,函数y=x2与函数y=alnx的图像有一个交点,方程f(x)=0有惟一解;当 a＞e时,函数y=x2与函数y=alnx的图像有两个交点,方程f(x)=0有两解.

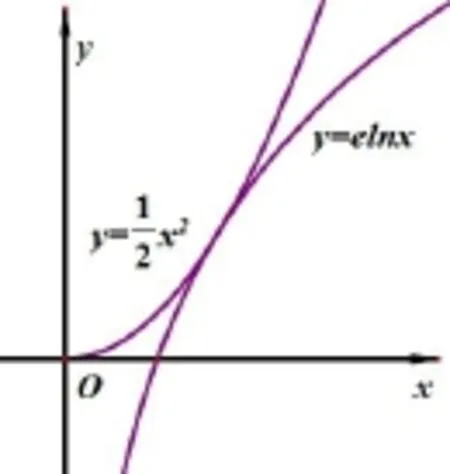
图1

四、利用切线求参数的取值范围

例5.设f(x)=若关于x的方程f(x)-k|x|=0有三个不等的实根,则实数k的取值范围是( )

A. (e,2e) B. (e,+∞) C. (1,e) D. (-2e,e)

解方程f(x)-k|x|=0有三个不等的实数根 ⇐⇒ 函数f(x)图像与函数y=k|x|图像有三个交点.作出它们的图像如图所示,可以看出,当x＜0时,若y=k|x|=-kx图像位于曲线y=-x2-2ex在x=0处的切线y=-2ex的下方,即-k＞-2e时,在y轴左侧总有一个交点;而当x≥0时,若y=k|x|=kx图像位于曲线y=ex过原点的切线y=ex的上方,即k＞e时,在y轴右侧总有两个交点.综上,所求实数k的取值范围为e＜k＜2e.

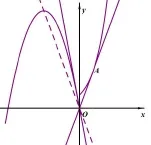
图2

五、利用切线求最值

例6. 直线y=a分别与曲线y=x2-lnx和直线y=x-2交于点P,Q,则|PQ|最小值为( )

解如图3,过点P作PM垂直直线y=x-2于点M,由于直线y=x-2的倾斜角为45°,故|PQ|=|PM|,从而只需求出曲线y=x2-lnx上的动点P到直线y=x-2的距离的最小值.我们将直线y=x-2平移至与曲线 y=x2-lnx相切时,切点P即为所求.于是y′=2x-=1=⇒ x=1,即P(1,1),从而.

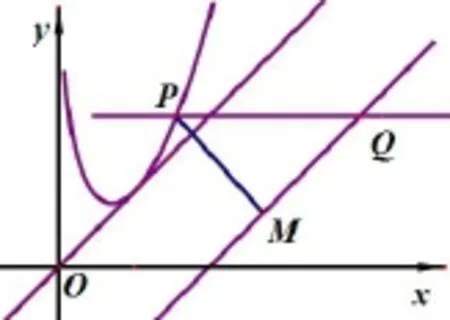
图3