函数极值点偏移问题的处理策略

江西省赣州市赣县区教师进修学校(341100) 马跃进

函数极值点偏移问题的处理策略

江西省赣州市赣县区教师进修学校(341100) 马跃进

函数极值点偏移问题,是近几年高考及各种模考题压轴的热点,交汇数学中函数的性质及应用、求导、方程、参数变换、不等式求解等技巧,很多学生对待此类问题经常是束手无策.而且此类问题变化多样,题型中又含有诸多参数,更平添了求解的难度.

笔者试通过本文,给出函数极值点偏移的定义,并借助微积分的思想方法探究函数极值点偏移问题的一般性求解方法,现将有关研究写在下面,供读者参考.

一、极值点偏移的有关概念

首先,我们来了解函数极值点偏移的特征,并给出函数极值点偏移的定义.

1.函数极值点偏移的基本特征：是指单极值函数,由于函数极值点左右的增减速度不同,使得函数图像没有轴对称性.如图1所示.

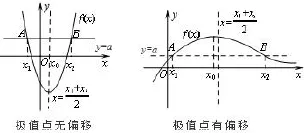
图1

2.函数极值点偏移的定义：已知函数f(x)有唯一的极值点(x0,f(x0)),直线y=a与函数y=f(x)交于不同两点A(x1,a),B(x2,a),设AB的中点为,若,就说函数f(x)在x=x0处的极值点有偏移.

3.函数极值点偏移的分类(已知条件如2)：

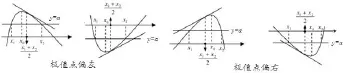
图2

构造函数F(x)=f(x0+x)-f(x0-x),x∈(-λ,λ),其中λ=|x2-x1|max(下同),易知F(x)是区间(-λ,λ)上的奇函数,以下称F(x)为极值点偏移关联函数.

二、极值点偏移关联函数的应用

例1(2010天津理)已知函数f(x)=xe-x(x∈R),如果x1/=x2,且f(x2)=f(x2),证明：x1+x2＞2.

解析因为 f′(x)=,易知当x＜ 1时, f′(x) ＞ 0;当 x ＞ 1时,f′(x)＜0,即f(x)在(-∞,1)上单调递增,在 (1,+∞)上单调递减.因为函数f(x)在x=1处取得极大值f(1),且f(1)=,如图3所示.

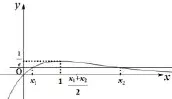
图3

由f(x1)=f(x2),x1/=x2,不妨设x1＜x2,则必有0＜x1＜1＜x2,构造函数F(x)=f(1+x)-f(1-x),则F(x)是R上的奇函数.

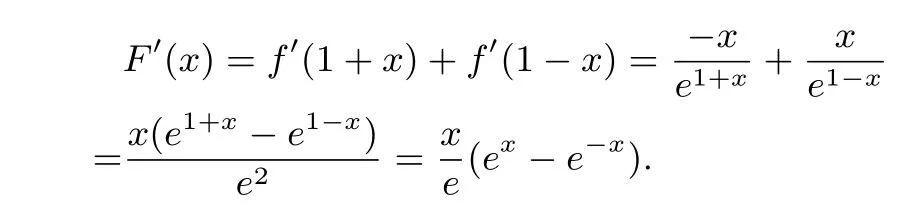
因为x=0时,F′(x)=0,x/=0时,x与ex-e-x同号,所以F′(x)≥0,即F(x)在R上单调递增,当x∈(0,+∞)时, F(x)＞F(0)=0,也即f(1+x)＞f(1-x)对x∈(0,1]恒成立.由0＜ x1＜ 1＜ x2,则1-x1∈(0,1],所以f(1+(1-x1))=f(2-x1)＞f(1-(1-x1))=f(x1)= f(x2),即f(2-x1)＞f(x2),又因为2-x1,x2∈(1,+∞),且f(x)在(1,+∞)上单调递减.故2-x1＜x2,即x1+x2＞2.

例2已知函数f(x)=x-aex有两个不同的零点x1,x2,求证：x1+x2＞2.

解析函数f(x)的两个零点,等价于方程xe-x=a的两个实根,从而这一问题与例1完全等价.

例3已知函数f(x)=lnx-ax,a为常数,若函数f(x)有两个零点x1,x2.试证明：x1·x2＞e2.

解析消参转化成无参数问题：f(x)=0⇐⇒ lnx= ax⇐⇒ lnx=aelnx,x1,x2是方程f(x)=0的两根,也是方程lnx=aelnx的两根,则lnx1,lnx2是x=aex的两根.设u1=lnx1,u2=lnx2,g(u)=ue-u,则g(u1)=g(u2),从而x1x2＞e2⇐⇒ lnx1+lnx2＞2⇐⇒ u1+u2＞2,此问题等价转化成为例1.

.

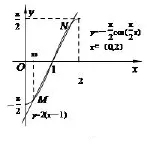
图4

所以 x0是 f(x)在区间 (0,1)上唯一的极小值点. x1+x2＞2x0⇐⇒ 函数f(x)的极值点左偏.由f′(x0)=0得

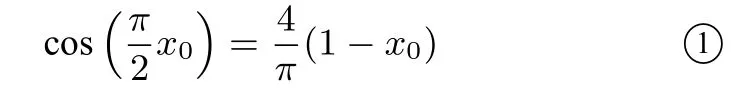
不妨设0＜x1＜x0＜x2＜1,函数f(x)极值点偏移关联函数为F(x)=f(x0+x)-f(x0-x),x∈(-1,1),则F(x)是奇函数. ,即

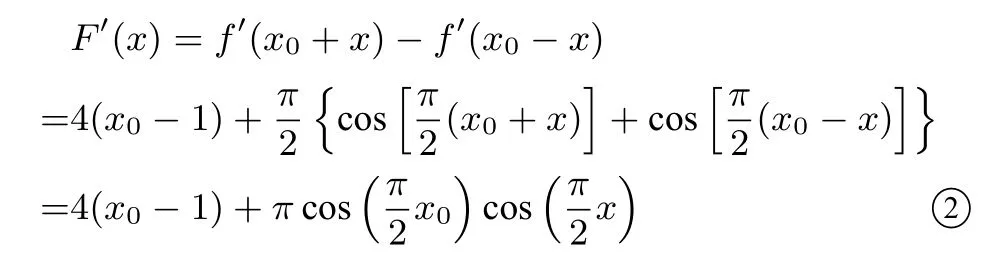
将①代入②得

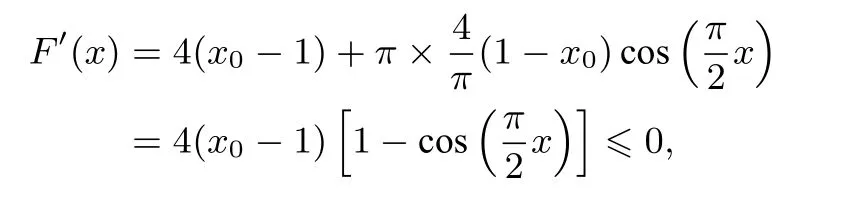
即F(x)在(-1,1)上单调递减,当x∈(0,1)时,F(x)＜F(0)=0,也即f(x0+x)＜f(x0-x)在区间(0,x0]上恒成立.由0＜ x1＜ x0＜ x2＜ 1,则x0-x1∈(0,x0],所以f(x0+(x0-x1))=f(2x0-x1)＜f(x0-(x0-x1))=f(x1)=f(x2),即f(2x0-x1)＜f(x2),又因为2x0-x1,x2∈(x0,1),且f(x)在(x0,1)上单调递增.故2x0-x1＜x2,即x1+x2＞2x0,命题得证.

例5 设函数f(x)=ex-ax+a(a∈R),其图像与 x轴交于 A(x1,0),B(x2,0)两点,且 x1＜ x2.证明：＜0.

即F(x)在(-λ,λ)上单调递增,当x∈(0,λ)时,F(x)＞F(0)=0,也即f(lna+x)＞f(lna-x)在区间(0,lna]上恒成立.由1＜x1＜lna＜x2,则lna-x1∈(0,lna],所以f(lna+(lna-x1))=f(2lna-x1)＞f(lna-(lnax1))=f(x1)=f(x2),即f(2lna-x1)＞f(x2),又因为2lna-x1,x2∈(lna,+∞),且f(x)在(lna,+∞)上单调递增.故2lna-x1＞x2,即＜lna,命题得证.

例7 (2016年新课标I卷理数压轴21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点x1,x2.证明：x1+x2＜2.

解析由f(x)=(x-2)ex+a(x-1)2,得f′(x)= (x-1)(ex+2a),可知f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.要使函数y=f(x)有两个零点x1,x2,则必须a＞0.函数有唯一的极小值点(1,-e),所证结论为函数极值点右偏.

只需构造极值点偏移函数F(x)=f(1+x)-f(1-x),x∈R,因为

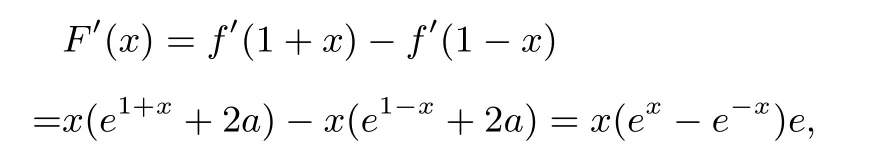
而x=0时,F′(x)=0;x/=0时,x与(ex-e-x)同号,所以F′(x)≥ 0,即F(x)在R上单调递增.所以f(1+x)＞f(1-x)在R上恒成立.不妨设x1＜1＜x2,则f[1+(1-x1)]＞f[1-(1-x1)]=f(x1)=0=f(x2)即f(2-x1)＞f(x2),又因为2-x1,x2∈(1,+∞),且f(x)在(1,+∞)上单调递增.故2-x1＞x2,即x1+x2＜2.

三、函数极值点偏移问题再思考

由上述探究易知,极值点偏移取决于关联函数F(x)=f(x0+x)-f(x0-x),x∈(-λ,λ),的单调性.而F(x)是其定义域上的奇函数,由微积分的基本性质易知F′(x)及∫F(x)dx均为区间(-λ,λ)的偶函数,都极具很好的图形对称性.

思考1 笔者的研究,仅仅从探究极值点偏移关联函数F(x)的导函数F′(x)入手,得到求解极值点偏移问题的一类方法,若从研究极值点偏移关联函数F(x)的积分函数∫F(x)dx入手,势必可以得到求解极值点偏移问题的另类方法.

思考2 在求解极值点偏移问题时,若构造另一个关联函数G(x)=f(x)-f(2x0-x),x∈(x0-λ,x0+λ),则函数G(x)的图像关于点(x0,0)中心对称,且函数G(x)的导函数G′(x)、积分函数∫G(x)dx的图像都关于直线x=x0对称,研究函数G(x)的单调性,也不失为求解极值点偏移问题的一种好方法.

期待对此问题感兴趣的读者,作进一步的探究.