数学文化高考题举隅(II)*
2017-04-05北京丰台二中100071甘志国
北京丰台二中(100071) 甘志国
数学文化高考题举隅(II)*
北京丰台二中(100071) 甘志国
1.5 勾股定理
题目22(1979年高考全国卷文科、理科第4题)叙述并证明勾股定理.
解勾股定理:直角三角形两直角边的平方和等于斜边的平方.
下面给出三种证法:
证法1 (中国古代数学家赵爽给出的证明)简述如下:
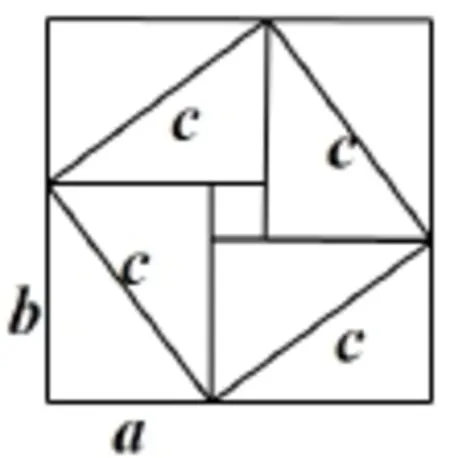
图18
证法2 (美国第二十任总统JamesAbramGarfield(1831~1881)于 1881年给出的证明)简述如下:
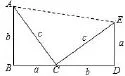
图19
证法3 如图20所示,圆O是Rt△ABC的内切圆,有.
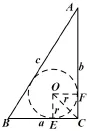
图20
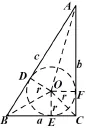
图21
注由证法3的思路,还可给出余弦定理的证明(2011年高考陕西卷文科、理科第18题就是“叙述并证明余弦定理”):
在△ABC中,分C为锐角、直角、钝角及S△ABC=.
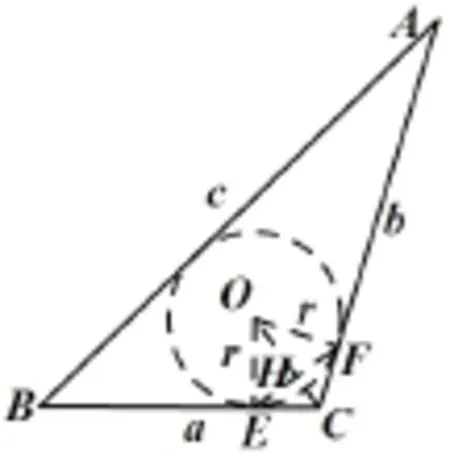
图22
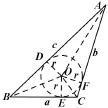
图23

1.6 蝴蝶定理
题目23 (2003年高考北京卷理科第 18题)如图24,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(b>r>0).
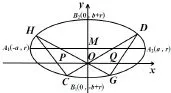
图24
(1)写出椭圆的方程,求椭圆的焦点坐标及离心率;
(2)直线y=k1x交椭圆于两点C(x1,y1),D(x2,y2) (y2>0).直线y=k2x交椭圆于两点G(x3,y3),H(x4,y4) (y4>0).求证:;
(3)对于(2)中的C,D,G,H,设CH交x轴于点P,GD交x轴于点Q.求证:|OP|=|OQ|.
(证明过程不考虑CH或GD垂直于x轴的情形.)
解(1)椭圆方程为,左、右焦点的坐标分别为F1(-√a2-b2,r),F2(√a2-b2,r),离心率

评析本题的背景是蝴蝶定理.蝴蝶定理最先是作为一个征求证明的问题,刊载于1815年的一份通俗杂志《男士日记》(Gentleman’sDiary)第39-40页上;而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,由于其几何图形形象奇特,貌似蝴蝶,便以此命名.
蝴蝶定理的内容是:如图25所示,圆O的弦PQ的中点为M,过点M任作两弦AB,CD,弦AD与BC分别交弦PQ于点X, Y,则M为线段XY的中点.
有意思的是,直到1972年以前,人们对蝴蝶定理的证明都并非初等且十分繁琐.至于初等数学的证法,在国外出现的资料中,一般都认为是由一位中学教师斯特温首先给出的面积法证明.1985年,在河南省《数学教师》创刊号上,杜锡录(1941~1994)教授以《平面几何中的名题及其妙解》为题,载文向国内介绍蝴蝶定理,从此蝴蝶定理在神州大地到处传开.
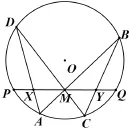
图25
下面介绍一种较为简便的初等证法:
如图26所示,作OS⊥AD于 S,OT⊥BC 于 T,连 结OX,OY,MS,MT,OM.
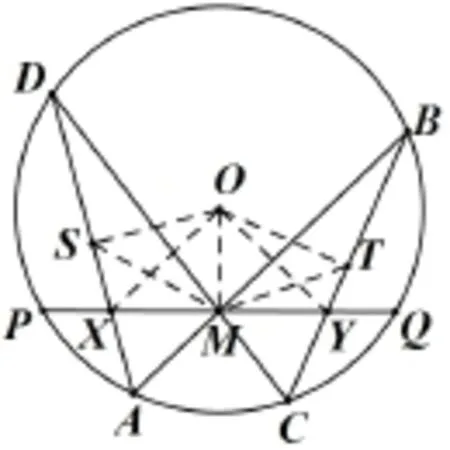
图26
再由M是弦PQ的中点,可得OM⊥XY,所以M为线段XY的中点.
实际上,还可把蝴蝶定理推广到任意的圆锥曲线中:
若过圆锥曲线Γ的弦AB的中点M 任作两条弦CD,EF,直线CE,DF与直线AB分别交于点P,Q,则|MP|=|MQ|.
证明如图 27所示,以M为坐标原点,直线AB为y轴,建立平面直角坐标系xMy.
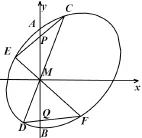
图27
可设圆锥曲线Γ的方程为ax2+bxy+cy2+dx+ey+f=0.再设A(0,t),B(0,-t)(t>0),得t,-t是关于y的方程cy2+ey+f=0的两个根,所以c/=0,e=0.
当直线CD,EF的斜率有不存在的情形时,可得欲证结论成立.

1.7 杨辉三角
题目24 (2006年高考湖北卷理科第15题)将杨辉三角中的每一个数都换成,就得到一个如图28所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出,其.
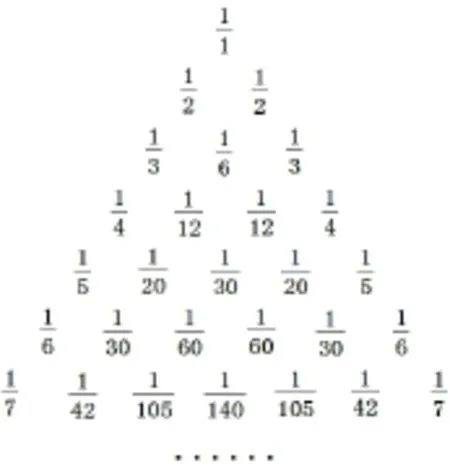
图28
答案.
评析显然该题有数学史背景,莱布尼茨(Gottfriend WilhelmvonLeibniz,1646~1716)是德国数学家、哲学家,同英国数学家、物理学家、天文学家牛顿并称为微积分学的创始人,他所创造的微分和积分符号一直沿用至今.杨辉是中国南宋末年的一位杰出数学家、数学教育家,杨辉三角是杨辉(?~1298)的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴含了许多优美的规律.而高中生对这些大数学家应当有所了解.
本题重在考查考生的观察能力和用等价转化思想解题.
题目25 (2007年高考湖南卷理科第15题)将杨辉三角中的奇数换成1,偶数换成0,得到如图29所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,...,第n次全行的数都为1的是第___行;第61行中1的个数是____.

图29
解2n-1,32.
由不完全归纳法知,全行都为1的是第2n-1行;因为26-1=63,所以第63行共有64个1,逆推知第62行共有32个1,并且是101010···01(共63个数)的形式(也可用不完全归纳法),再归纳出第61行是11001100···110011(共62个数)的形式,知共有32个1.
评析本题难度较大,考查不完全归纳法.要想彻底弄清每个组合数的奇偶性是很困难的.
题目26 (2004上海春季高考第11题)如图30,在由二项式系数所构成的杨辉三角形中,第____行中从左至右第14与第15个数的比为2:3.
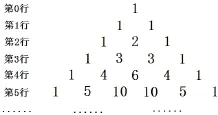
图30
答案34.
1.8 多边形数
题目27 (2009年高考湖北卷文科、理科第10题)古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:

图31

图32
他们研究过图31中的1,3,6,10,···,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图32中的1,4,9,16,···这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A.289 B. 1024 C.1225 D. 1378
答案C.
题目28 (2012年高考湖北卷文科第17题)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图31所示的三角形数:
将三角形数1,3,6,10,···记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2012是数列{an}中的第____项;
(2)b2k-1=____.(用k表示)
答案(1)5030;(2).
题目29 (2013年高考湖北卷理科第14题)古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,···,第n个三角形数为.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
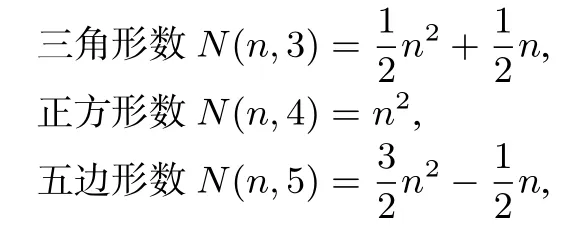
六边形数N(n,6)=2n2-n,
······
可 以 推 测 N(n,k)的 表 达 式,由 此 计 算N(10,24)=___.
答案1000.
评析这三道高考题都涉及古希腊人研究过的多边形数.且题目27、题目28均源于普通高中课程标准实验教科书《数学5·必修·A版》(人民教育出版社,2007年第3版)(下简称《必修5》)第28页.题28和题29主要考查考生的观察、猜想、验证的解题能力.
小学生也可解答题27这道选择压轴题:只需考查m2(m∈N∗)及1+2+···+n=n(n+1)(n∈N∗)的2倍n(n+1)的个位数字便可用排除法求解.
若解答此题的一般情形,还需要用到不定方程中的佩尔方程[3]知识.
1.9 祖暅原理
题目30 (2013年高考上海卷理科第13题)在xOy平面上,将两个半圆弧(x-1)2+y2= 1(x≥1)和(x-3)2+y2=1(x≥ 3)、两条直线y=1和y=-1围成的封闭图形记为D,如图33中阴影部分.记D绕y轴旋转一周而成的几何体为Ω,过(0,y)(|y|≤1)作Ω的水平截面,所得截面面积为4π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为____
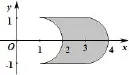
图33
解2π2+16π.由几何体为Ω的水平截面面积为,它由两部分组成.
由祖暅原理可得,几何体Ω中对应部分的体积就是该圆柱体的体积,即2π2.
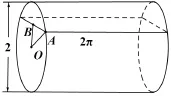
图34
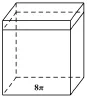
图35
第二部分为定值8π.如图35所示,图35表示底面积为8π、高为2的长方体(其体积为8π·2=16π).由祖暅原理可得,几何体Ω中对应部分的体积就是该长方体的体积,即16π.所以几何体Ω的体积为2π2+16π.
评析祖暅 (公元前 5~6世纪),字景烁,祖冲之(429~500)之子,范阳郡蓟县(今河北省涞源县)人,南北朝时代伟大的科学家.他继承刘徽(约225~295)和祖冲之的工作,解决了球体积的计算问题,与其父共著《缀术》.在天文学方面,曾测量日影长度,发现北极星与北天极不动处相差一度有余,纠正了北极星就是北天极不动处的错误观点.主要著作有《漏刻经》一卷、《天文录》三十卷(均已失传).
祖暅在数学上的突出贡献是他在实践的基础上,于5世纪末提出体积计算原理(祖暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是,如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.祖暅提出上面的原理,要比其他国家的数学家早一千多年.在欧洲直到17世纪,才有意大利数学家卡瓦列利提出上述结论.(见《必修2》第30-31页.)
1.10 错位数
题目31 (1)(2004年高考湖北卷文科第11题)将标号为1,2,···,10的10个球放入标号为1,2,···,10的10个盒子里,每个盒内放一个球,恰好3个球的标号与其在盒子的标号不一致的放入方法种数为( )
A. 120 B. 240 C. 360 D. 720
(2)(2004年高考湖北卷理科第 14题)将标号为1,2,···,10的10个球放入标号为1,2,···,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有____种.(以数字作答)
答案(1)B.(2)240.
评析这两道小题实质相同,背景都是“错位数”[4](数学家欧拉和丹尼尔·伯努利(DanielBernoulli,1700~1782)都研究过错位数).记n个元素的错位数为Dn,可得D1=0,D2=1,D3=2,D4=9.这两道题有相同的解法:.
1.11 欧拉公式
题目32 (2014年高考陕西卷理科第14题)观察分析下表中的数据:
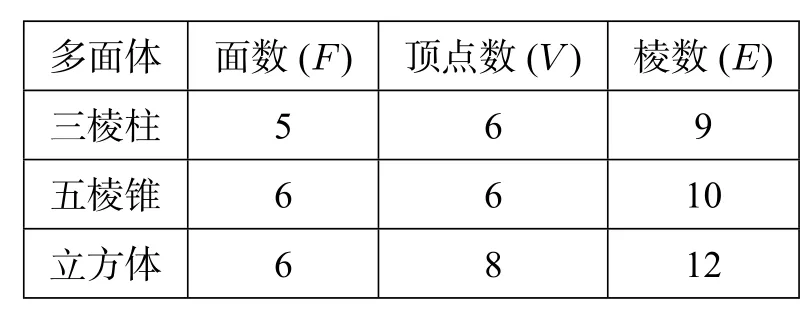
多面体面数(F)顶点数(V)棱数(E)三棱柱5 6 9五棱锥6 6 10立方体6 8 12
猜想一般凸多面体中F,V,E所满足的等式是___.
答案F+V-E=2.
评析本题考查合情推理中的归纳.欧拉是瑞士数学家、自然科学家.生于瑞士的巴塞尔,在俄国圣彼得堡去逝.13岁时入巴塞尔大学学习,是约翰·伯努利(JohannBernoulli, 1667~1748)的学生,15岁大学毕业,16岁获得硕士学位.欧拉是18世纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把整个数学推至物理的领域.他是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等的课本,《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作.欧拉对数学的研究如此之广泛,因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理.此外,欧拉还涉及建筑学、弹道学、航海学等领域.瑞士教育与研究国务秘书CharlesKleiber曾表示:“没有欧拉的众多科学发现,今天的我们将过着完全不一样的生活.”法国数学家拉普拉斯(Pierre-SimonLaplace,1749~1827)则认为:读读欧拉,他是所有人的老师.
1.12 割圆术
题目33 (2010年高考湖北卷理科第7题)如图36所示,在半径为r的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去.设Sn为前n个圆的面积之和,则=( ) A. 6πr2B. 4πr2C.D. 2πr2
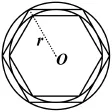
图36
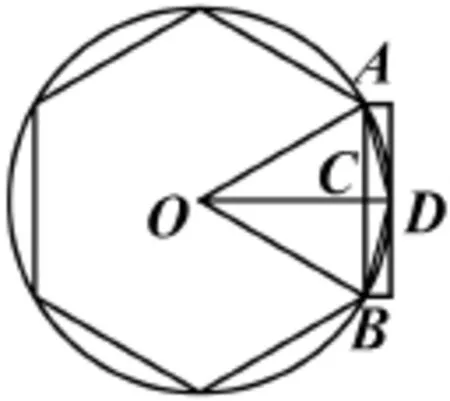
图37
答案B.
评析此题有中国古代数学家刘徽(约225~约295)的割圆术这一数学史(如图37所示)的背景.
刘徽的一生是为数学刻苦探求的一生.他终生未曾做官,故称为“布衣”;但他人格高尚,治学严谨,堪称楷模,万世师表.他不是沽名钓誉的庸人,而是学而不厌的伟人,他给我们中华民族留下了宝贵的财富,不愧是中国古代一位杰出的布衣数学大师[5].
本题考查的知识是求等比数列的前n项和及数列极限.
《必修3》第45-47页介绍了割圆术.
1.13 皮克公式
题目34 (2013年高考湖北卷文科第17题)在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图38中△ABC是格点三角形,对应的S=1,N=0,L=4.
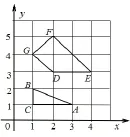
图38
(1)图中格点四边形DEFG对应的S,N,L分别是___;
(2)已知格点多边形的面积可表示为S=aN+bL+c,其中a,b,c为常数,若某格点多边形对应的N=71,L=18,则S=____.(用数值作答.)
答案(1)3,1,6.(2)79.
评析本题的背景是皮克(GeorgePick,1859~1943,奥地利数学家)公式:顶点是整点(横坐标、纵坐标均是整数的点叫做整点)的多边形(可以是凸多边形也可以是凹多边形)的面积是S=a+-1,其中a表示多边形内部的点数,b表示多边形边界上的点数.
题目35(2014年高考湖北卷第理科21题)(2014年高考湖北卷文科第22题)π为圆周率,e=2.71828···为自然对数的底数.
(2)(文)求e3,3e,eπ,πe,3π,π3这6个数中的最大数与最小数.
(理)将e3,3e,eπ,πe,3π,π3这6个数按从小到大的顺序排列,并证明你的结论.
答案(1)增区间为(0,e),减区间为(e,+∞).
(2)(文)所求最大数与最小数分别是3π,3e.
(理)3π>π3>eπ>πe>e3>3e.
评析第(1)问是经典问题,2013年高考北京卷理科第18题、1983高考全国卷理科第九题、2005年高考全国卷III理科第6题、2001年高考全国卷理科第20题都与此函数有关,由此函数的单调区间可得经典问题“比较ab与ba的大小”的简洁结论:
(1)当0<a<b≤e时,ab<ba;
(2)当e≤a<b时,ab>ba;
(3)当-0<a≤1且a<b时,ab<ba;
(4)当1<a<e且b>e时,ab<ba,ab=ba,ab>ba均有可能.
另外,该题中的六个幂涉及数学中的两个重要常数e和π(e<3<π),所以本题“美丽无比”.
题目36 (1)(2015年高考安徽卷文科第7题)执行如图39所示的程序框图(算法流程图),输出的n为( )
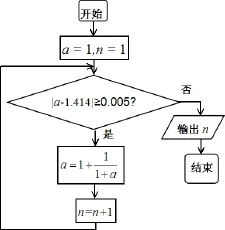
图39
A. 3 B. 4 C. 5 D. 6
(2)(2015年高考安徽卷理科第13题)执行如图39所示的程序框图(算法流程图),输出的n为____.
答案(1)B.(2)4.
评析本题的背景是人类历史是发现的第一个无理数即的无限连分数的前四个渐进分数.
1.15 阿基米德三角形
题目37 (2015年高考全国卷I理科第20题)在直角坐标系xOy中,曲线C:与直线l:y=kx+a(a>0)交于M,N两点. (1)当k=0时,分别求C在点M和N处的切线方程; (2)y轴上是否存在点 P,使得当 k变动时,总有∠OPM=∠OPN?说明理由.
答案(1)和.(2)存在点P(0,-a)符合题意.
题目38 (2007年高考江苏卷第19题)如图40,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A,B两点.一条垂直于x轴的直线,分别与线段AB和直线l:y=-c交于点P,Q.
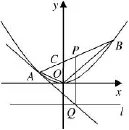
图40
(2)若P为线段AB的中点,求证:QA为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由.
答案(1)c=2.(2)略.(3)(2)的逆命题成立,理由略.
题目39 (2006年高考全国卷II理科第21题)已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(2)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
答案(1).(2),S的最小值是4.
题目40 (2005年高考江西卷理科第22题)如图41,设抛物线C:y=x3的焦点为F,动点P在直线l:x-y-2=0上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
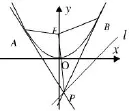
图41
(1)求△APB的重心G的轨迹方程;
(2)证明∠PFA=∠PFB.
答案(1)3y=4x2-x+2.(2)略.
评析题37~40的背景都是阿基米德三角形(抛物线的弦与该抛物线在该弦的端点处的两条切线围成的三角形叫做阿基米德三角形).阿基米德最早利用逼近思想证得了结论:抛物线的弦与抛物线围成的封闭图形的面积是相应的阿基米德三角形面积的.阿基米德三角形的众多性质是编制高考试题的源泉,读者可参见文献[6]-[9].
1.16 方格几何学
题目41 (2014年高考福建卷文科第12题)在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L-距离”定义为||P1P2||=|x1-x2|+|y1-y2|,则平面内与x轴上两个不同的定点F1,F2的“L-距离”之和等于定值(大于||F1F2||)的点的轨迹可以是( )
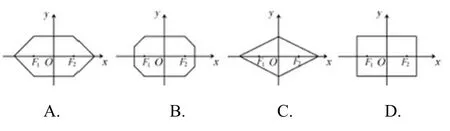
答案A.
题目42 (2006年高考福建卷理科第12题)对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:||AB||=|x1-x2|+|y1-y2|.
给出下列三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2= ||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
答案B.(①正确)
题目43 (2010年高考广东卷理科第 21题)设A(x1,y1),B(x2,y2)是平面直角坐标系xOy上的两点,现定义由点A到点B的一种折线距离ρ(A,B)为ρ(A,B)= |x1-x2|+|y1-y2|,对于平面xOy上给定的不同的两点A(x1,y1),B(x2,y2):
(1)若点C(x,y)是平面xOy上的点,试证明ρ(A,C)+ ρ(C,B)≥ρ(A,B);
(2)在平面 xOy上是否存在点 C(x,y),同时满足:quan1ρ(A,C)+ρ(C,B)= ρ(A,B);②ρ(A,C)= ρ(C,B).若存在,请求出所有符合条件的点;若不存在,请予以证明.
答案(2)存在,即线段AB的中点.
评析题目41~43的背景都是方格几何学.方格几何学是由生于俄国的著名德籍数学家闵可夫斯基(Hermann Minkowski,1864~1909)最先开始研究的.文献[10]简单介绍了方格几何学.
[1]张奠宙.多一点数学文化的考题[J].数学教学,2015(9):封底
[2]甘志国.高考压轴题(上)[M].哈尔滨:哈尔滨工业大学出版社, 2015.28-29
[3]甘志国.湖北高考数学卷与世界名题相通[J].数学教学,2009(11):46-48
[4]甘志国.为2010年的高考数学湖北卷叫好[J].数学通讯,2010(8下):46-50
[5]甘志国.中国古代杰出的布衣数学大师刘徽[J].新高考(高一·数学(必修1)),2016(10):14-15
[6]殷加兴.阿基米德三角形初探[J].中学数学研究(江西),2009(12)4页
[7]邵明志,陈克勤.高考试题中的阿基米德三角形[J].数学通报, 2008(9)
[8]王学凤,刘晓锐.悄然兴起的阿基米德三角形[J].高中数学教与学, 2009(5)
[9]丁益民.一道高考试题引发的探究与思考[J].数学通讯,2010(10下)
[10]甘志国.有趣的方格几何[J].新高考(高二·数学),2013(11):39-40
*该文为连载文章,共有三个部分,这是其中的第II部分—编者注.
