例说不等式的几种证明方法
2017-04-05安徽省无为县牛埠中学238351朱小扣
中学数学研究(广东) 2017年5期
安徽省无为县牛埠中学(238351) 朱小扣
例说不等式的几种证明方法
安徽省无为县牛埠中学(238351) 朱小扣
对不等式的考察一直是高考和竞赛的热点,不等式的证明方法也有很多,大多数同学经常会觉得难以掌握.为此,本文将从几个简单的例子出发,阐述解不等式的几种方法,以期给初学者有所帮助,不对之处,欢迎指正.

方法二(赫尔德不等式)
证:由赫尔德不等式可得:

所以

即证.
方法三(待定系数法)
分析尝试找到一个r,使得:成立,故只需.依条件可知原不等等号成立时,a=b.为了找出r,可先令b=1得:.再令:.求导:
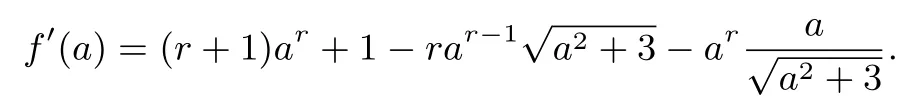

证

故

①+②即证.
用切线法还可以证明2015年高中数学联赛安徽省初赛第9题:
解题思路(切线法)证即可.(注:在处的切线方程是y=2-x)
有时除了用切线法外还可以用割线法:
例三已知 a,b,c∈ R+,a+b+c=1,求证:.
方法五(割线法)可知在两点的割线方程是,故只需证在(0,1)上恒成立即可.

割线法还可以证明如下例题:
解题思路(割线法)只需证≤1+a ⇐⇒a(3a+2)(a-1)≤0(0≤a≤1)(注:f(x)=在 (0,1),(1,2)两点的割线方程是y=x+1)
上面阐述了证明不等式的五种方法,除此之外还有像柯西不等式,贝努利不等式等多种方法,证明方式也是千变万化,本文只是阐述最基础的方法.事实上,不管数学题目怎样变化,但只要我们掌握其本质,就能一招制敌,学生必须具有一题多解,多题一解的能力,这样才能在做题时,多角度,多思维的去考虑,才能在做题中达到自身水平的提高!希望本文能对初学者有所帮助.
[1]韩京俊.初等不等式的证明方法[M].哈尔滨工业大学出版社, 2014,2.
