把握学习起点 聚焦思维难点
——“翻转课堂”理念下《平行四边形的面积》教学设计与思考
2017-04-01王丽兵
王丽兵
《平行四边形的面积》是人教版五年级上册《多边形的面积》单元的学习内容之一。它是在学生初步认识了平行四边形后,围绕面积对平行四边形的进一步研究,它也是后续学习三角形面积、梯形面积的知识基础。教材以平行四边形面积的公式推导为主要内容,以活动操作体验为主要形式,注重新旧知识间的转化与沟通。从这个角度来讲,在整个小学数学“图形与几何”领域中,这一内容实质是起到了承前启后的重要作用。
一、学生起点分析
一方面,在长方形和正方形面积的学习过程中,学生已经积累了通过数面积单位来描述图形面积的经验。与以往数面积单位不同的是,平行四边形中首次出现不完整的“半格”,这对于学生无疑是一种挑战,同时这也是转化思想培养的有效载体。另一方面,由于长方形和正方形的面积计算,虽然有所区别,但从本质上来讲都属于“邻边×邻边”,这也就为较普遍的“平行四边形的面积=邻边×邻边”的观点找到了最合理的解释。显然,平行四边形的面积无论是“邻边×邻边”,还是“底×高”,都已经成为本课教学的现实生态。
基于此,这些都为“平行四边形的面积”的“翻转”学习提供了诸多有利的条件和资源支持。因此,笔者从以生为本的角度出发,翻转学习,改变学习方式,以求做一些突破。
二、教学过程设计
1.分享成果:感知图形转化意义。
师:同学们的学习任务单完成了吗?那让我们先在四人小组内交流一下自己的学习收获和问题吧!不过,老师在这里对大家的交流提两点小建议,你可以这样来表达:
◇我设计的平行四边形是这样的……
◇我是用这样的办法数出平行四边形的面积的……
【说明:通过课堂学习基础现状的讨论,以相对民主和平等的方式讨论明确本节课学习交流的方式。同时,规范学生的语言表达,提高学生学习交流的能力。】
师:老师课前也浏览了一些同学的预学作品,一起来看一下:
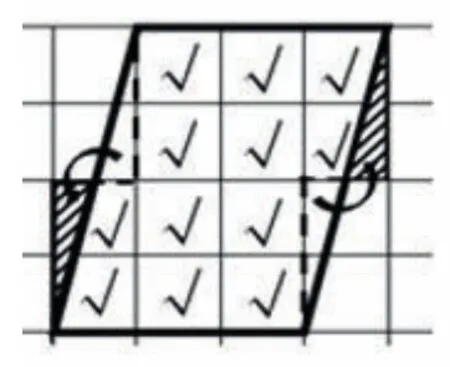
图1
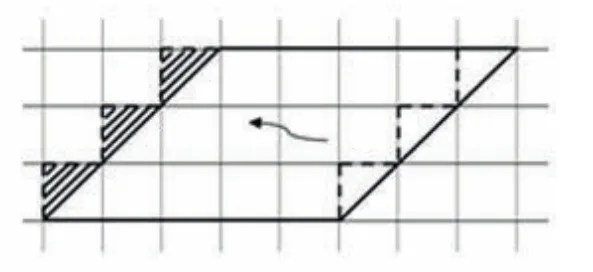
图2
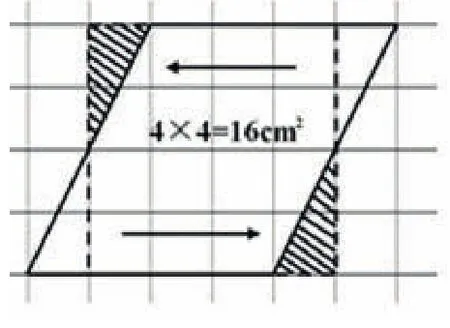
图3
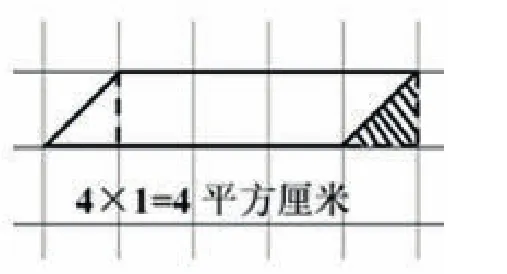
图4
师:大家看懂这四幅作品了吗?能说说他们分别是怎样数出了平行四边形的面积吗?
生:图1通过旋转的方式,将不满整格的部分,拼成完整的图形,这样每层有3个正方形,一共有4层,所以是12平方厘米。或者,他给每个方格都打“√”,说明也可以一个一个数出来。
生:图2是将右边不满格的部分平移到了左边,使它们变成完整的一格。拼成以后每层有5个方格,一共有3层,所以面积是3×5=15平方厘米。
生:图3通过平移以后得到了一个边长是4厘米的正方形,所以,他是用“4×4”计算出平行四边形的面积的。
生:图4通过平移以后得到了一个长是4厘米、宽是1厘米的长方形,所以她是用“1×4”计算出平行四边形的面积的。
【说明:通过对“学习单”中学生作品的选择,笔者有意引导学生对高、矮、胖、瘦,不同形状和方向的平行四边形进行观察和讨论,使得学生明确“不满整格”的部分是可以通过平移、旋转进行拼组的,令原来的图形面积单位更方便计数。】
师:现在请大家观察一下这几位同学在数平行四边形面积的时候,有什么共同特点?
生:他们都把平行四边形改变了一下,使不满整格的全都拼成了整格的图形。
生:它们有些还变成了我们以前学习过的长方形或正方形。
师:那么转化以后的长方形和正方形,与原来的平行四边形相比,什么变了?什么没有变?
生:形状变了,面积的大小没有变。
教师小结:这种现象,我们在数学里称之为“转化”(板书)。
【说明:通过对四个不同形状的平行四边形的整体观察,使得学生能够体验到平行四边形“不满整格”的部分都是需要转化成长方形的,并且这个长方形与原来的平行四边形的面积大小是一样的。】
2.答疑解惑:突破知识理解难点。
师:分享了学习成果,我们来看一下同学们提出的问题:
(1)如果格子多了,该怎么办呢?
(2)平行四边形是不是只能切成三角形来拼?
(3)如果一个平行四边形特别斜,那面积怎么数?
(4)将平行四边形拉成一个长方形,可以用邻边相乘的方法计算吗?
师:你能解决哪些问题呢?
生:第一个问题,如果方格特别多,我们可以把它们转化拼成比较规整的图形,然后计算即可。
生:第二个问题,我觉得也可以切成两个梯形,它们也能够拼成一个长方形。但剪的时候应该沿着高来剪才可以。
师:为什么呢?难道随便切不行吗?
生:随便切就不能拼成比较规则的长方形或者正方形了。
生:第三个问题是担心平行四边形太斜,沿着高竖着切下来会切到图形的外面,接下来就很难平移或者旋转拼成完整的图形了。
生:不能沿着高竖切,也可以沿着横的高,横切呀!只是这个长方形是斜的。
师:那对于第四个问题你怎么看?
师:暂时不能回答没关系!那我们就重点来研究一下。现在请你选择问题三或问题四其中一个研究,等会儿我们要进行反馈,来表达你自己的观点。针对问题四,老师这里还有一个微视频,你们研究完了想要验证一下或者遇到问题了,可以上来点击观看。
【说明:以自主选择的方式,针对学生困惑的问题展开研究讨论,重点帮助学生加深对于“邻边相乘”和特殊平行四边形面积计算问题的理解,以突破学生在思维理解上的难点。】
师:研究问题三的同学,对于这样特别斜的平行四边形,你们是怎么数它面积的呢?

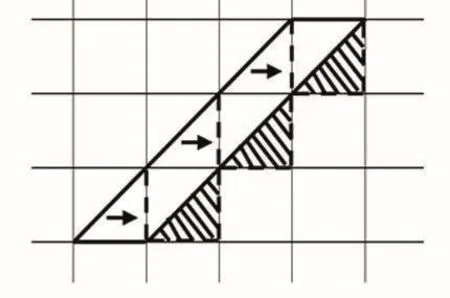
师:那对于问题四大家是怎么研究的?结论是什么?
生:将下图中的深色三角形平移到左边,将它的空缺补齐,上面斜线部分就是多出来的面积。

生:将平行四边形拉成长方形和原来的平行四边形面积不一样。
生:这是因为原来平行四边形的高变长了,所以面积变大了。
师:那将平行四边形往下压呢?
生:平行四边形的面积会变小,因为它的高变短了。
师:对于用邻边相乘来计算平行四边形的面积,大家怎么看?
生:这是不行的,因为面积变化了,所以不能代表原来平行四边形的面积。
【说明:通过对“剪拼”和“拉动”两种方法的对比研究,使得转化思想在面积研究过程中的意义进一步凸显。尤其是对拉动形成的长方形的观察和比较,使得平行四边形面积的变化变得愈加直观和形象,更加凸显“高的变化”对于图形面积变化的作用,留给学生的印象更深刻。】
3.反思回顾:梳理知识学习方法。
师:回顾整节课,大家说说看,我们是怎么学习的?和以往有什么不同?
生:我们先看了微课视频,做了一份课前学习单。然后在课堂上一起分享了我们的预学成果。之后还专门研究、讨论、解决了同学们提出的一些问题。
师:那到底平行四边形的面积应该怎么计算呢?你是怎么想到的?
生:平行四边形的面积=底×高。
生:转化后的长方形面积 =长×宽。
师:到底哪个对呢?
生:“长×宽”算得是转化以后长方形的面积,“底×高”算得是平行四边形的面积。
【说明:通过对学习过程的回顾,不仅有助于学生对于平行四边形面积计算意义的理解,而且对于新的学习方式的提炼概括,也能有助于学生学习能力和素养的提升。】
三、教学实践反思
1.以微课视频为载体,前置知识学习。
学生对于平行四边形并不陌生,但对其面积计算的认识和理解,大部分学生还只是停留在“只知其然,不知其所以然”的状态。因此,笔者有意通过微课视频内容的学习,避开一些和本课学习无关的非本质因素,直奔学习主题。不仅较为直观地向学生介绍了平行四边形面积的意义,并且通过“设计尽可能多形状不同的平行四边形,再清楚地表示出它的面积”为任务,驱动学生进行自主实践和思考。一方面,可以帮助教师了解和掌握学生的知识起点和思维难点;另一方面,也为后续的操作和探究活动积累经验并形成丰富的生态资源。
2.以任务驱动为形式,激化转化需求。
如何激发学生认知的矛盾,激发学生图形转化的需要,从而实现学生思维认知的直观外显,这是本节课笔者力求能够有所突破的又一思考。因此,笔者设计以“数”面积为学习任务,激发学生对于平行四边形转化的需求。其中,既包括一般形状的平行四边形,也包括特殊(特别斜)的平行四边形。简单来说,笔者有意帮助学生通过“数”平行四边形面积,一方面“数”出规律经验,积累方法意义的普遍性;另一方面要“数”出层次,激发认知冲突,感受方法意义的特殊性。显然,从课堂生成的资源来看,学生为了更方便的“数”,生成了诸如割补、旋转、平移等多种方法。不仅为本课学习提供了丰富的学习素材,同时也为平行四边形和长方形的面积关系的讨论埋下伏笔。
3.以问题疑惑为抓手,强化意义理解。
通过对学生学习问题的梳理和解答,重点围绕“为什么不能用邻边相乘的方法来计算呢?”进行探讨。应该说,“拉动转化”突破了学生对于原有“割补转化”认知的现状,不仅能够激发起思维认知冲突,而且也能引起学生对于等积转化本质的关注。因此,笔者有意从学生的问题入手,结合平行四边形模型框架的操作拉动,直接聚焦“邻边相乘”本质的意义,关注学生思维的难点。通过起初的操作观察,再结合课中微课视频的学习,使得学生逐步感受到“拉动”平行四边形,虽然底边和周长没有发生变化,但由于高的长度的变化,使得平行四边形面积也相应地发生了变化。不仅使学生对于平行四边形面积计算的认知更全面和立体,也令本课思维的难点得到了关注和突破。
