多样情境 多元表征 多维考量
——《分数的初步认识》教学案例(一)
2017-04-01陈瑾
陈 瑾
【教学内容】
人教版三年级上册第90、91页。
【课前思考】
分数的初步认识是在学生认识了万以内的数、掌握平均分和倍的知识的基础上进行的教学。分数的认识分为两个学段来教学:三年级上册主要是借助操作和直观,从“部分——整体”的角度初步认识分数;五年级下册则是在此基础上使学生从感性认识上升到理性认识,概括出分数的意义,并在表达“部分——整体”意义的基础上,进一步从测量、比和商等角度认识分数的含义。
认识几分之一是认识几分之几的基础,是整个单元的起始课。学生掌握了分数的基本知识,感悟数形结合的数学思想和方法,发展数感,为三年级下册初步认识小数和五六年级进一步理解并掌握分数的意义、用乘除法解决分数问题打下良好的基础。
从整数到分数是对数概念的一次扩展。对于学生而言,“分数”并不是全然陌生的概念,但与学生整日打交道的整数相比,二者无论在意义上还是读写方法及计算方法上都有很大差异。相对于整数而言,分数概念较为抽象而且有多种理解方式,并非是可以通过计数活动得到的一个数,而是代表了两个量关系的相对量。学生要真正理解什么是分数,并不是一件简单的事。
影响学习的唯一重要的因素,就是要探明学习者已经知道了什么,并应据此进行教学。所以,在设计这节课时,我一直在思考:以我班学生的学习基础与学习能力,能否创设最简单的情境,引导学生在直观感受与动手操作中理解什么是分数。踏踏实实,步步为营,更多的感受和更新的体验自然而然地渗透在每一个环节,这样才能让不同层次的学生都有所得,享受到数学带给自己的成就感和快乐。
【教学过程】
一、微课导入,整体感知分数
师:同学们,这两年来我们一直在和整数打交道,今天我们一起来认识一种新的数——分数(板书:认识几分之一)。想必同学们在生活中已接触过分数,关于分数,你知道些什么呢?请大家说一说。
生:我知道分数的写法,上面有分子,下面有分母,就像妈妈背着孩子一样。
生:分母和分子中间还有一条横线,但我不知道叫什么。
生:分数有无数个,有的分数比1小,有的分数比1大。
……
师:分数在我国很早就有了,最初分数的表示法和现在可不一样,请同学们一起来了解分数的发展历史。(播放微视频)
师:看了这段视频,你对分数的了解是不是更多了?对照之前同学们的发言,说说你的收获。
(学生各抒己见,逐步完善自己的认知结构。教师顺势教学分数的读写、各部分的名称)
师:生活中常常能见到分数。你能找出下列句子中的分数吗?请写出来。
1.我们已经吃掉这个蛋糕的二分之一。()
2.美国约三分之一的成年人被认为是过度肥胖。()
3.上学期,我们班有四分之一的同学当上三好学生。()
4.这一期的黑板报中,“习作园地”占整个黑板报的八分之一。()
(集体反馈)
【设计意图:来自学生的素材最是鲜活灵动,以开放的姿态引导学生参与知识的建构与生成,以更积极的态度从不同的角度接纳与分析信息。而视频中分数的发展史实际上也是人类社会文明的发展史,对学生的视觉与心灵都是一次冲击,类似动漫的效果也备受学生的喜欢。之后的分数读写教学则是水到渠成。】
二、动手操作,初步探究分数
1.认识二分之一。
将学生作品展示到黑板上:

师:涂色部分的含义是什么?
生:我把这张纸看成一个蛋糕,平均分成两份,涂色部分表示已经吃掉的。
师:你特别强调了“平均分”。如果不平均分呢?
师:你抓住了分数学习的最关键处,非常棒!那空白部分表示什么呢?
生:空白部分表示剩下的蛋糕。吃掉和剩下的各占一半,所以都用来表示。
师:真棒!可是为何大家画的方法不一样,却都能表示出已经吃掉这个蛋糕的呢?
引导学生理解:不管分得的形状是怎样的,只要是把一个整体平均分成两份,里面的每一份都是整体的。
师:是不是只有这三种分法呢?
生:我发现只要找到这个正方形的中点,过中点画一条线,无论怎样画,都能将这个正方形平均分成两份,每份都是这个整体的,所以有无数种分法。
2.创造几分之一。
(教师指定全班三大组的学生用自己喜欢的方式分别表示余下三道题中的分数,并说说这个分数的含义)
(学生独立思考后动手操作。教师巡视,指点需要帮助的学生)
(教师有选择性地反馈学生作品,并请三名同学上台解释自己画的图是什么意思)
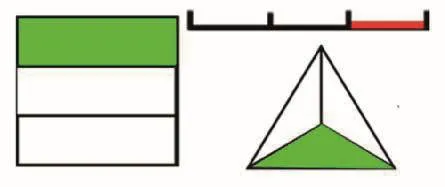
生:把所有美国成年人平均分成三份,有一份是过度肥胖,用分数表示。
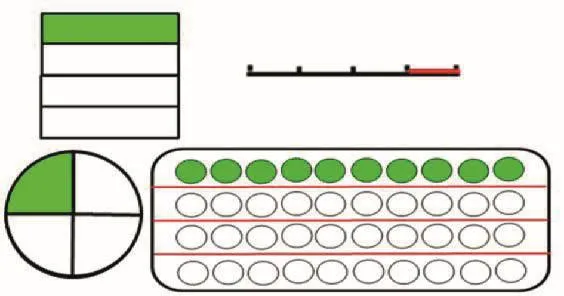
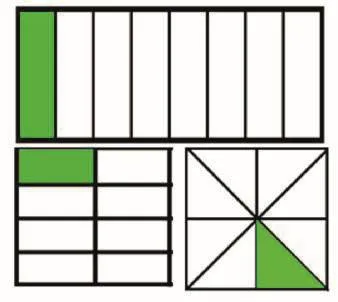
生:把整个黑板平均分成八份,有一份是“习作园地”,用分数表示。
(在解释图意的过程中,教师要注意及时纠正学生不规范的或错误的表达,强调“平均分”“分的是谁就是谁的几分之几”)
3.比较几分之一。
(1)比较同分母分数的大小。
出示下图:你从这幅图中能看到哪些分数?


(2)比较同分子分数的大小。
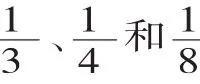

再出示一组线段图和一组圆形,既是不完全归纳,又能验证刚才学生的结论。


4.几分之一变式练习。
下列说法对吗?请你判断并说说理由。

(1)上图中的阴影部分不能表示“我们班有四分之一的同学当上三好学生”。()
有的同学一开始认为这两道题都是正确的,理由是:第一题每份形状不同,所以阴影部分不能表示出整体的四分之一。第二题的两个二分之一肯定相等。教师不置可否,静观其变。
生:第一题不对,虽然每份形状不同,但是确实是将整个图形平均分成了四份,阴影部分表示其中的一份,所以能表示出整体的四分之一。
生:第二题中并没有说两个班的总人数一定相等,所以两个二分之一也不一定相等。比如405班有40人,女生就有20人,406班有42人,女生就是21人,女生人数不相等。所以这道题也是错的。
师:在什么情况下,这道题就肯定正确呢?
生:必须是两个班的总人数相等的前提下,这道题才是正确的。
【策略分析:分数概念具有双重性,既有“数的特征”,也有“形的特征”。只有从两个方面认识分数,才能很好地理解并掌握它的本质意义。教师不仅要通过示范让学生去感受几何直观的价值,更应该鼓励学生积极利用各种图形去直观分析和解决问题。经历独立尝试、交流共享、碰撞完善的过程,积累利用图示学习数学的经验,并用个性化的方式来记录和表达自己的思维过程,学生的思辨能力与思维的缜密性就能得到较好的培养与发展。】
三、综合应用,加深理解分数
1.完成练习二十第二题。
【设计意图:从“用一张正方形纸(或线段、圆片等)表示出四分之一”到“根据一个整体的四分之一画出整个图形”,正向到逆向,一来一回,使“平均分”“分的是谁就是谁的几分之几”两重意思的理解得到深化,帮助学生形成“带得走”的能力。】
2.完成练习二十第八题。
【策略分析:各图形不易直接看出平均分了几份,且阴影部分分散出现,组合起来比较复杂,需要通过平移、旋转、对称等变换重新组合,这样的练习可以培养学生灵活解决问题的能力,同时也渗透了分数的计算。】
3.七巧板是同学们熟悉的玩具,你从中发现了哪些分数呢?
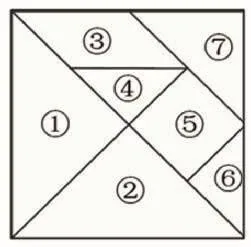

(1)()号图形占整个正方形的();()号图形占整个正方形的();
我还能继续写:()号图形占整个正方形的()。
(2)我还发现:()号图形相当于()号图形的( )。
【策略分析:创设特定的学习情境,将七巧板与数学完美融合,引导学生打开思路,一句提示,一条辅助线,不需要更多言语,此时无声胜有声。】
