几何直观：提高学生思维能力的磨刀石

牛向华

借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中发挥着重要作用。几何直观是学生直观理解数学的手段，它是一种意识、手段，也是一种思维方式。在小学阶段，几何直观主要通过数形结合的思想来体现。

一、“玩”中感知

在一年级的《重叠问题》中有这样的情境：你看，穿花衣服的大雁多漂亮呀！从前面数，它排在第6；从后面数，它排在第3。这一行大雁一共有多少只呢？

为了帮助学生理解问题情境，展现学生的思维，可以让学生通过演一演、摆一摆、画一画等活动初步感知几何直观。

1.演一演：举手的同学为“花大雁”。

2.摆一摆：通过具体实物的摆一摆，学生初步感知用直观的信息呈现数学问题。

3.画一画：有的学生用△代替花大雁，用○代替其他大雁。

通过演一演、摆一摆、画一画，学生很容易看出，花大雁被数了两次，即重叠了一次，因此可以这样列式解决重叠问题5+3=8（只）或 6+3-1=8（只）。

通过画一画，把具体事物抽象成几何图形，摆脱了实物的束缚，让学生体会画图的形象性、简洁性和简便性，并用“形”刻画和解释了问题，做到了数形结合，使几何直观在学生心中开始萌芽，学生闻到了几何直观的气味。

二、“思”中成长

如：在《简单的搭配问题》中，学生经历了几何直观辅助自己有序思考的全过程，体会到了几何直观的必要性。

师：2件上衣和3条裙子一共有多少种搭配方法呢？你能通过摆一摆找到答案吗？

生：

师：每次用学具摆很麻烦，怎么办？

生：连一连。

师：实物太麻烦了，能不能想个办法再简单些！

生：可以用符号或图形代替！

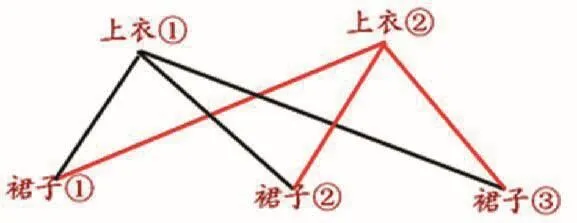
学生在一步步的方法优化中，经历了有序思考和符号化的过程，此间几何直观起到了非常重要的作用。学生通过摆一摆的实物直观理顺了2配3的顺序，然后再去体会这种顺序还可以用更简单的方式表达出来，做到数形的完美结合，几何直观在学生心中逐渐成长。

三、“用”中提升

在《植树问题》一课中，学生在用几何直观辅助理解题意的过程中，数学思想方法也悄然入心。

师：20米的小路，每5米栽一棵树，一共可以栽多少棵树？你能自己画图试试吗？

生：

师：生活中还有没有像这样的植树问题呢？

生：站队的时候有植树问题。

生：插彩旗的时候有植树问题。……

师：我们来看看刚才大家提到的这些问题是不是植树问题呢？

生：它们都是植树问题，有“树”也有“间隔”。

学生们通过几何直观把实物图抽象成线段图，较好地体会了一一对应思想。并且很清楚地感受到“树”与“间隔”，还能迅速地将它们归为一类问题，很好地体会了模型思想。在用几何直观解决问题的过程中，学生的思维得到了训练，数学素养得到了提升。

四、“练”中自觉

在有了初步感知、亲历体验、素养提升的基础上，学生还要在平时的数学学习中自觉去应用，让几何直观成为一种思维习惯，以便更好地帮助自己分析问题、解决问题。

例如文中一开始提到的案例，如果学生有用几何直观解决问题的习惯，哪怕在头脑中想象出线段图的样子或记住植树问题这种数学模型中段数与次数的关系，都会轻松准确地解决问题。

再如，在一次练习中有这样一道题：仓库里有一批货物，第一次运走这批货物的，第二次运走9吨，此时运走的货物与剩下的货物吨数的比是7:5。这批货物一共有多少吨？正在很多学生束手无策找不到解题思路时，已经有部分同学做出来了。我让其中一名学生板演时，他就用到了画线段图这种几何直观思想分析数量关系的方法，轻而易举地解决了问题

当然，学生有能力水平和思维风格的差异，面对相同的问题，会出现不同的方法，表现出不同的思维特点，我们也不必强求所有学生用几何直观的方法来表征问题、探索思路。在日常的练习中，几何直观作为一种实践经验，还要逐步内化为思维经验，从而成为一种思维自觉。

几何直观能力的培养需要我们教师在读懂教材、了解编者意图的基础上，在教学中长期关注，并有意识地渗透。首先我们要选好“点”，即几何直观在哪里用。几何直观作为一种手段或工具，我们要明确它用在什么地方最恰当。我们要有效预设教学，选好几何直观能力培养的点，这样会起到事半功倍的效果。其次我们更要把握好“度”，即用到什么程度停止。数学的本质是抽象与推理，所以直观不是我们的目的，借助几何直观实现抽象的思维发展才是我们的最终目的。几何直观完成自己的任务就要迅速抽身让位于抽象或者推理，否则将会限制学生的思维发展。我们还要让学生感受几何直观在数学学习中的作用，感受它的优势，逐渐将几何直观转化为数学学习的内在需要。

总之，几何直观能力的培养是一个持续的过程，如果我们从一年级开始就坚持并适当地渗透、引导，在数学思考过程中，学生的头脑中就会逐步有一个看不见的“形”的支撑，逐渐形成几何直观的意识、能力和思维方式，从而提升学生的数学素养。