用数学建模思想组织教学——《“两积之和结构”的应用问题》教学设计

陈　慧

【教学内容】

浙教版四年级应用问题之“两积之和结构”。

【教学过程】

一、课前谈话

师：上学期我们学了三步计算的应用问题，今天我们来研究其中的一类——“两积之和结构”的应用问题。

（板书课题：“两积之和结构”的应用问题）

师：看到“两积之和结构”你有什么想问的？

生：什么叫“两积之和结构”？

生：“两积之和结构”的问题有哪些？怎么解决？

二、新授

1.逐步呈现“两积之和结构”。

第一环节：

师：老师家的两块玻璃不小心打破了，现在老师想配这两块玻璃。要想知道应该付给玻璃店老板多少钱，你认为需要知道什么？

生：要想知道总价钱，我们需要知道玻璃的单价，以及待配玻璃的总面积。

（出示课件，单位cm，下同）

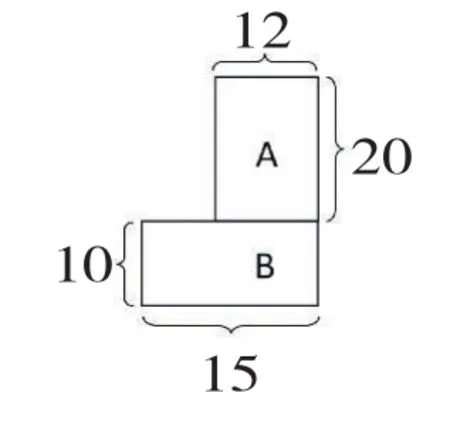
师:现在能求出玻璃的总面积吗？怎么求？

生：要求两个长方形的面积和，可以先分别计算出长方形A和B的面积，也就是12×20和15×10，然后把它们的积加起来，算式是：12×20+15×10=390。

（教师引导学生观察算式结构，得出“积+积=和”的结构，也就是“两积之和结构”）

第二环节：

（出示课件）

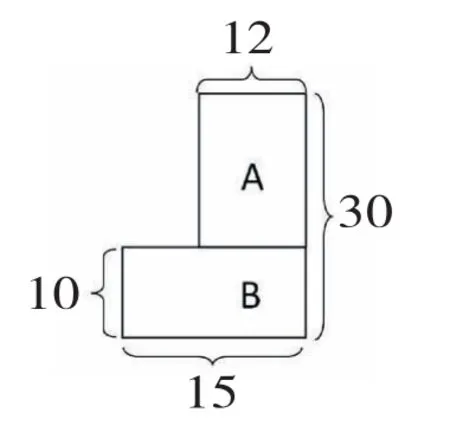
师：和前一幅图相比，这幅图有什么变化？你还能求出A、B的面积和吗？

生：这道题没有直接给出A的宽。

师：这个问题是“两积之和结构”吗？

生：是两积之和，只是其中的一个信息要间接求得。

［学生独立尝试，教师展示并讲评：15×10+（30-10）×12］

第三环节：

（出示课件）

师：这回又有什么变化？有发现吗？

生：第一幅图告诉我们A、B的长、宽，求它们的面积和；现在A、B的面积和，B的长、宽以及A的长知道，要求A的宽。

师：还是这几个数量，只不过把原来未知的变成已知的；把原来已知的一个信息，变成未知的问题。

（学生独立尝试的基础上，教师指名展示、讲评）

生：（390-10×15）÷20=12。

生：10×15+20×？=390。

师：我们先看“10×15+20×？=390”，能看懂吗？

生：10×15就是 B的面积，20×？就是A的面积，合起来是 390cm2。

师：那么“（390-10×15）÷20=12”是什么意思呢？

生：390减去B的面积就是A的面积，然后用面积除以长求出A的宽。

生：这两种算法是一样的。“10×15+20×？”表示了题目本来的意思，“（390-10×15）÷20”就是求解“？”的过程。

师：你们认为这道题是不是“两积之和结构”的问题？

生：是“两积之和结构”的逆向问题。

板书:▲×20+10×15=390

▲=（390-10×15）÷20

2.鸡兔同笼问题。

（出示图：观察已知和未知）

生：15×▲+12×●=390。

生：15×▲表示B的面积，12×●表示A的面积，390是面积和。

生：图中还告诉我们▲+●=30，所以我建议把等式改成：15×▲+12×（30-▲）=390。

（教师引导学生结合图，解释等式各部分表示的意思）

师：我们怎么来求▲表示多少呢？

（视班级基础，结合图形引导求解）

3.比较与联系。

师：（整体呈现四个问题）它们有什么联系与区别？

生：都是“两积之和结构”，可以把直接信息变为间接信息，也可以从正向求和变为逆向求取其中一个数量。

小结：数学中有很多问题实质上是同一类数量结构，只是做了一些变化，我们只要抓住本质，就能化繁为简、化难为易。

三、巩固应用

1.读一读，想一想，下面的问题和前面“两积之和结构”的图像有什么联系？

商品　单价　数量A 20　12 B 15　10总价　？

生：A的单价和数量相当于A长方形的长和宽，A的总价相当于A长方形的面积；B同此理。本题和第一幅图表示的结构一样。

师：第一幅图除了可以表示总价和，还可以表示什么？谁能再用图里的信息编一道应用问题？

工作问题：师傅每小时做20个零件，做了12小时，徒弟每小时做15个零件，做了10小时，师徒一共做了多少个零件？

行程问题：一艘小货船，先以每小时20千米的速度行12小时，又以每小时15千米的速度行10小时，终于从A地到达B地。A、B两地相距多少千米？

……

2.买8件羊毛衫和7件衬衣共付1646元，1件羊毛衫120元，1件衬衣多少钱？

师：你会做吗？和“两积之和结构”的问题有什么关系？

生：这道题是“两积之和”逆向问题。

师：你能用题目里的这些信息，通过间接条件或者方向变化，改编出哪些应用问题？又分别如何求解？请在作业本上写一写，算一算。

四、全课小结（略）

【编辑点评】

多步应用问题一直是小学数学学习中的一个难点。基本数量关系一经复合，错综复杂，变化多端。张天孝老师经过长期研究，梳理出小学数学应用问题复合关系的三大基本结构——“两积之和”“两商之差”“正反比例”。并基于这三大基本结构，通过情节性、扩缩性和可逆性变换，演绎出了绝大部分小学数学复合应用问题。这就以简驭繁，帮助广大教师抓住了应用题教学的“牛鼻子”。

陈慧老师这一节课，教学的正是其中的一种基本结构——“两积之和结构”。陈老师依托教材，牢牢把握住了其中的数学逻辑，同时又根据学生的认知特点，做了一些创造性的设计，使得教学情境更富童趣，教学层次更加丰富，值得学习。

引入部分，陈老师设计了一个“配玻璃”的现实情境，这个情境既真实又概括，可谓轻重合宜，一举两得。真实，可以激发学生参与的积极性；概括，可以较快切入面积图的分析与学习。

展开部分，陈老师借助面积图与等式表征，成功强调了“两积之和结构”及其变式。其中有三个细节显示出教的主导性和有效性。其一，面积图层级递进，设计得比较合理，变式落在多数学生的最近发展区，多数学生有尝试的积极性和可能性。其二，算术解法和代数解法沟通，用代数解法去点明结构，用算术解法锻炼逆向推理。其三，以多图整体呈现，比较联系作为课堂小结，引领学生跳出具体问题的解决，梳理问题的结构和发展脉络，做更高层次的反思和概括，培养批判性思维。

练习只有两题，内涵却很丰厚。第一题，发散思维，情境变换；第二题，逻辑推理，可逆变换。在变换中进一步强化“两积之和结构”，积累数学变式的经验，体会模型思想。

数学课有数学味：概括，使数学简明；变式，让数学丰满。在概括与变式之间自觉穿行，让我们的学生更加聪明！