平行四边形面积公式的推导过程

文|陆艾玲

在前测中，很多学生都认为平行四边形面积是邻边相乘。那么如何突破学生的认知冲突？可以采用下面的教学过程。

一、独立尝试，暴露问题

提供素材：练习纸上印一个平行四边形，底为6cm，斜边为5cm，高为4cm。

提出任务：测量需要边线的数据，计算平行四边形的面积。

预设学生有两种答案：

1.测量两条邻边的长度，再相乘，6×5=30cm2。

2.测量平行四边形的底和高，再相乘，6×4=24cm2。

二、针锋相对，聚焦本质

呈现以上两种答案，举手表决赞同哪种方法。

提出要求：你赞同哪种方法？想办法证明自己的方法是正确的，并说服对方。

思考：四根木条钉成的可拉动框架，从平行四边形拉成长方形过程中，什么变了？什么没有变？

图1

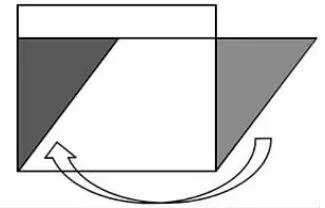
图2

小结：把平行四边形拉成长方形，四根木条的长度没有变，所以周长没变。通过割补法发现在拉动过程中面积变大了，所以长方形面积＞平行四边形面积。因此“邻边×邻边”求的是长方形面积，平行四边形则不能用“邻边×邻边”来计算。

三、借助格图，理解含义

把平行四边形衬上格子图，动态呈现剪拼的过程。（每个格子边长是1cm）

思考：在剪拼过程中，什么变了？什么没有变？

小结：在剪拼过程中，周长变短了，面积没有变。把平行四边形变成长是6cm、宽是4cm 的长方形，6×4=24cm2。

四、借助转化，掌握推导

思考：平行四边形有几组对应的底和高，你能找一找、量一量、算一算吗？

预设：两种剪拼方法。

①

②

引导学生建立对应：长方形的长就是平行四边形的底，长方形的宽就是平行四边形的高，长方形面积=长×宽，对应得到平行四边形面积=底×高。