这样的作业能预习吗

沈莉

缘起

开学第一天回家，读六年级的女儿就带回一项预习作业：制作等底等高的圆柱和圆锥。

作为家长的我，收到的短信是这样的：用卡纸分别做一个圆柱和圆锥，要求它们的底面积和高都相等（不能和数学书后面大小一样）。大小和方法要孩子通过预习后自己发现，家长只能在制作中打下手。老师的意图是：只有让孩子亲身体验制作过程，才能深入理解两个立体图形的特征。

于是乎，晚上7点，全家总动员。

女儿首当其冲，拿出一张完整卡片，卷起，把两条短边粘贴在一起，成了一个筒状。接着打算做底时，停了下来，盯着底面周长发愣。我观察着：虽然是知道长边就是底面周长，可刚才没有经过深思，虽然是粘好了，可现在却无法确定圆周长到底是多少了？想直接就圆筒上量直径，可纸有韧性，一动，圆就可能大了，也可能小了，无法得出正确值。第一次尝试失败。

有些经验了，只见她干脆先画好三个等面积的圆（两个用于圆柱，一个用于圆锥）。在思考中，完成了3个半径为4厘米的圆。这样一来，圆周长就是25.12厘米。于是，圆柱就在粘贴中勉强完成（此处忽略圆柱的美观性）。

接下来开始攻克圆锥：取出另一张卡纸，开始动手。一会儿下面长边连住，可上面怎么也汇聚不到一点；一会上面卷出一个尖点，可下面又相差十万八千里。摆弄了一会，絮絮叨叨：我来剪成三角形试试看。说时迟，那时快，只见她一对折，找到长边中点，然后“咔嚓咔嚓”分别从中点剪到长边的两端，顿时出现了一个等腰三角形。这个倒符合圆锥无论从正面还是侧面，观察到的都是等腰三角形结果。可是，底面周长是围好了，顶点也有了，可怎么侧面成了个“大豁嘴”？

我在一旁，已经有些按捺不住：“我们参考一下书后面吧。”于是，三下五除二，一下子惊呼：哦，原来圆锥的侧面是应该一个扇形。那好吧，现在知道弧长是25.12厘米，也知道是某个圆周长的一部分，可这个圆的半径是多少呀？圆心角又是多少呀？一筹莫展中。

这时，孩子也已经完全知晓（当然我们之前早就知道），这内容已经完全超出她的理解范围。百度上明确指出求弧长及扇形面积，隶属于九年级数学上册第2章《对称图形——圆》。在半径为R的圆中，弧长L与所对的圆心角度数n之间有如下关系：L=π/360×2πR=ππR/180。看来，现在要想在已知弧长的基础上，求出半径、圆心角是不可能了。

于是，我们和孩子商量：慢慢来，不着急，我们先试着做做书上的。

尽管，孩子很不情愿（因为老师说不能做书上的圆柱、圆锥），不过在我们“不唯上，不唯书，只唯实”的理念感召下，也完成了圆锥的制作。

这时，她倒又不急不躁，开始把玩圆锥，说：“妈妈，我绝对做不出老师要求的圆柱和圆锥了。你看，圆锥这么矮，怎么可能会和圆柱一样高呢？”只见，她拿出另外一张完整的卡纸，随手在长边处划了条弧线，接着随手卷卷。我们理解她想要表达：圆锥不可能会和圆柱一般高了，因为圆柱的高已经到达了巅峰。这时，她的脸上已经明显呈现出不自信的神情。

最终方案如下：调整次序，先完成圆锥的侧面，然后，照着圆锥的底面描画出一个圆形底面；同样也以这个底面为准，估摸着完成圆柱的侧面。

在这样瞎弄弄（女儿这般说）中，我们全家在晚上9点完成了老师布置的等底等高的圆柱和圆锥的制作。

思考

“圆柱和圆锥”是日常生活中常见的几何体之一，也是小学阶段立体图形教学内容的重要组成部分。教材（苏教版《数学》六年级下册）第9页例1教学圆柱和圆锥的特征。教材先教学圆柱再教学圆锥。对于圆柱，安排了两个层次的活动，引导学生由浅入深、由表及里地探索圆柱的特征。第一层次，结合实物图初步感知圆柱。第二层次，通过对圆柱的进一步观察，认识圆柱的直观图及其底面、侧面和高。

鉴于学生此前没有认识过圆锥，生活中接触圆锥形物体的机会也相对较少，所以教材在出示了生活中一些常见的圆锥形物体的同时，直接告诉学生“这些物体的形状都是圆锥体，简称圆锥”，并通过底注说明这里所指的圆锥都是直圆锥，以帮助学生初步建立圆锥的表象。接着要求学生说说生活中还有哪些圆锥形状的物体，使学生对圆锥的特征获得更丰富的感知。在此基础上，引导学生进一步观察圆锥，说说圆锥有什么特征，在交流中明确圆锥的特征，同时结合圆锥的直观图认识圆锥的顶点、底面、侧面和高。最后，让学生找一个圆锥，指出它的顶点和底面，以进一步强化认识。

手和脑在一块儿干，是创造教育的开始；手脑双全，是创造教育的目的。作为同年级数学老师的我，非常清楚这位教师在本课提出动手操作预习的意图：要求同学在预习过程中亲自动手实践，通过剪、拼、折、画、量、观察、比较等活动，体验、感悟新知识。同学亲身经历了立体图形形成过程，对圆柱、圆锥各部分名称及其特征，肯定可以了然于胸，甚至对后续学习也能起到一定的帮助。

可光有美好的愿望就可以实现目标了吗？第二天进行对此班级的回访，发现绝大多数同学是制作了一个圆柱、一个圆锥，可并不是等底等高的圆柱与圆锥，甚至还有同学反映：根本没有留意到等底等高这个条件。甚至与这位教师的交流，自己都直惊呼：没有考虑这么多！这样的预习作业，如何讲评，效果几何？

要学生做的事，教师躬亲共做；要学生学的知识，教师躬亲共学；要学生守的规则，教师躬亲共守。教师布置预习任务，对学生有这样那样的要求，可对自己有这样那样的要求吗？我想教师对自己应该更有高标准严要求，必须对相关内容进行认真研读，提出既有一定的价值，又有吸引力，能促使同学产生浓厚的学习、探索兴趣的预习任务。我认为，此老师任意提高预习要求，提出要求圆柱、圆锥等底等高这类难以解决的要求（虽然是为了后续发现等底等高的圆柱与圆锥之间的关系），却没有考虑学生实际学情。“先生的责任不在教，而在于教学，而在于教学生学。教的法子必须根据学的法子。先生不但要拿他教的法子和學生学的法子联络，并须和他自己的学问联络起来。”陶行知先生的教学箴言字字珠玑。

设想

身为家长、教师的双重身份的我，深深觉得教师布置预习作业一定要谨慎，注意难度适中，操作性强。尽管教育时机已过，可先进行好教学设计的设想。

为什么不能就地取材采用书本后面的圆柱、圆锥展开图呢？是怕学生只会拿着现成资料制作成圆柱、圆锥，就不能很好完成预习任务了吗？学生自己独立制作圆柱、圆锥就能很好完成预习任务了吗？我就设想先利用好这两张展开图，完成圆柱和圆锥。

当然还不仅仅如此。学习活动和结果是外显的，便于观察和比较。然而，发生在大脑中的思维活动却是内隐的，看不见也摸不着。如何在预习中让学生的思维过程外显呢？我觉得通过布置制作书后的圆柱、圆锥任务后，梳理一张学习单是非常必要的。

圆柱和圆锥的认识学习单

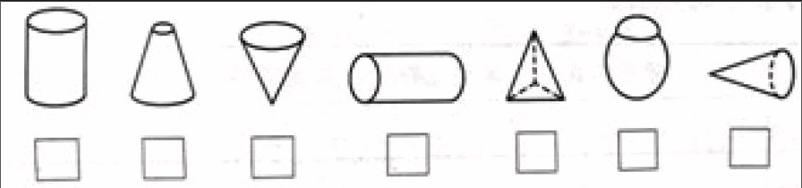
1.下面哪些是圆柱？哪些是圆锥？是圆柱的画“○”，是圆锥的画“△”。

2.填一填。

（1）圆柱的上、下兩个面叫作（ ），围成圆柱的曲面叫作（ ），圆柱的两个底面之间的距离叫作圆柱的（ ）。

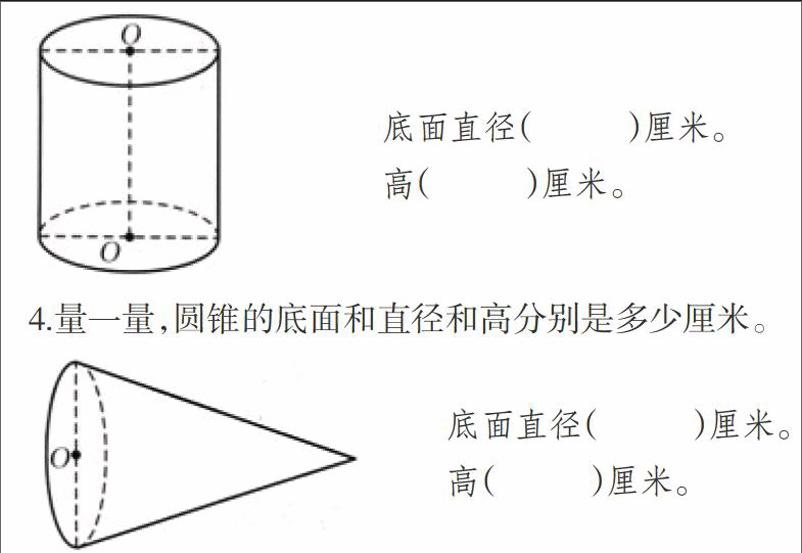
3.量一量，圆锥的地面直径和高分别是多少厘米。

4.量一量，圆锥的底面和直径和高分别是多少厘米。

还有后续。教学做是一件事，不是三件事。我们要在做上教，在做上学。不在做上用功夫，教固不成为教，学也不成为学。利用实践课，在学生掌握圆柱、圆锥知识的基础上，进一步巩固已学知识，并验证圆柱和圆锥的体积关系：

1.制作一个底面直径为5厘米、高为6厘米的圆柱。

2.制作一个底面直径为5厘米、高为6厘米的圆锥。

（1）先剪一个侧面（扇形）

①扇形的半径多长？

老师先告知学生扇形的半径R=6.5厘米。说明：这个问题到了中学就可以自己计算，现在若有兴趣，也可以课后探询。

②扇形的圆心角多大？

老师再次告知弧长公式：扇形的弧长=2πR×n°/360n°=15.7÷（2×3.14×6.5）×360°≈138.5°

（2）再制作一个底面（圆形）

3.证实圆柱和圆锥体积的关系。

现在我们制作好了圆柱和圆锥，它们有什么相同之处？那么它们的体积有何关系？

通过倒入大米，证实等底等高的圆柱和圆锥体积之间的关系。

课前预习是教师的一种教学手段，也是学生行之有效的学习方法，它能明显地提高学生学习的效率，激发学生自觉学习的主观能动性，获得课堂学习的主动权，从而达到优化课堂整体结构以至优化课堂细节的作用。教师根据教学的内容需要安排预习，请从教材特点、学情出发，着力在操作性、启发性、量力性，用心提炼预习步骤和内容，提出合理要求，能更好地体现素质教育理念，激发学生兴趣，促进学生全面发展。