让“等底等高的三角形面积相等”看得见

沈青 严秀丽

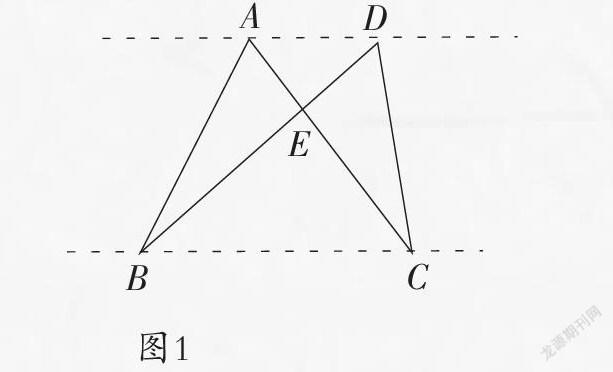
“等底等高的三角形，面积一定相等。”这是小学数学“图形与几何”板块中的一个著名的命题。在现行人教版教材小学数学五年级上册的练习题中，就有充分的体现（如图1）。

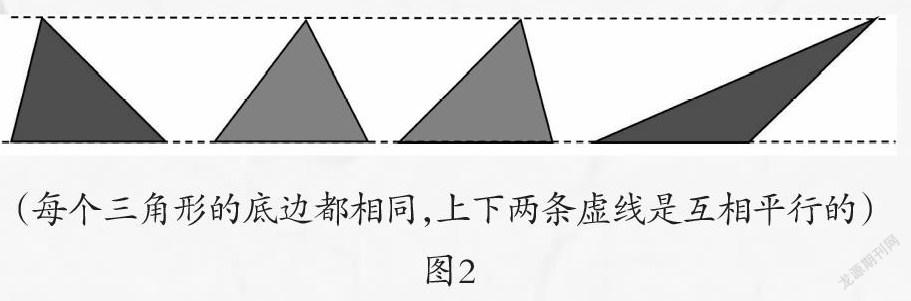
在实际的学习过程中，相当一部分学生是通过“赋值计算”的方法，“相信”等底等高的三角形面积相等。面对虽然等底等高、但形状各异的三角形，还是有一部分学生不敢坚信他们的面积是相等的（如图2）。因为在他们看来，这些三角形的形态差异实在是太大了。

（每个三角形的底边都相同，上下两条虚线是互相平行的）

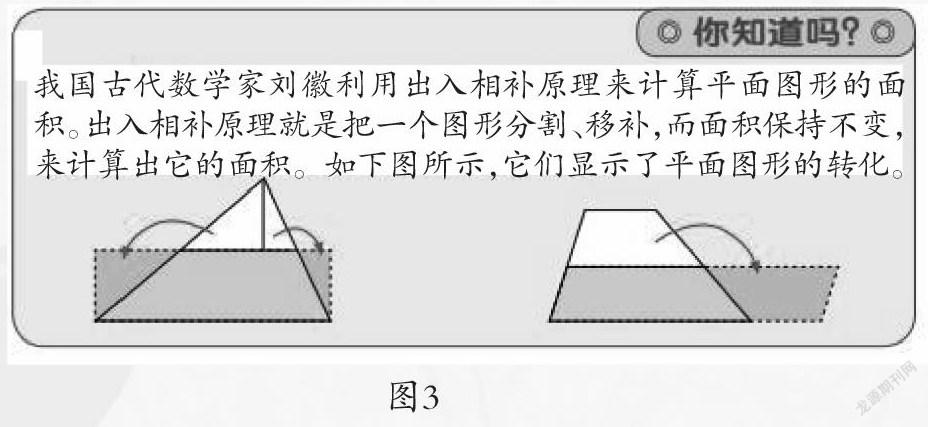
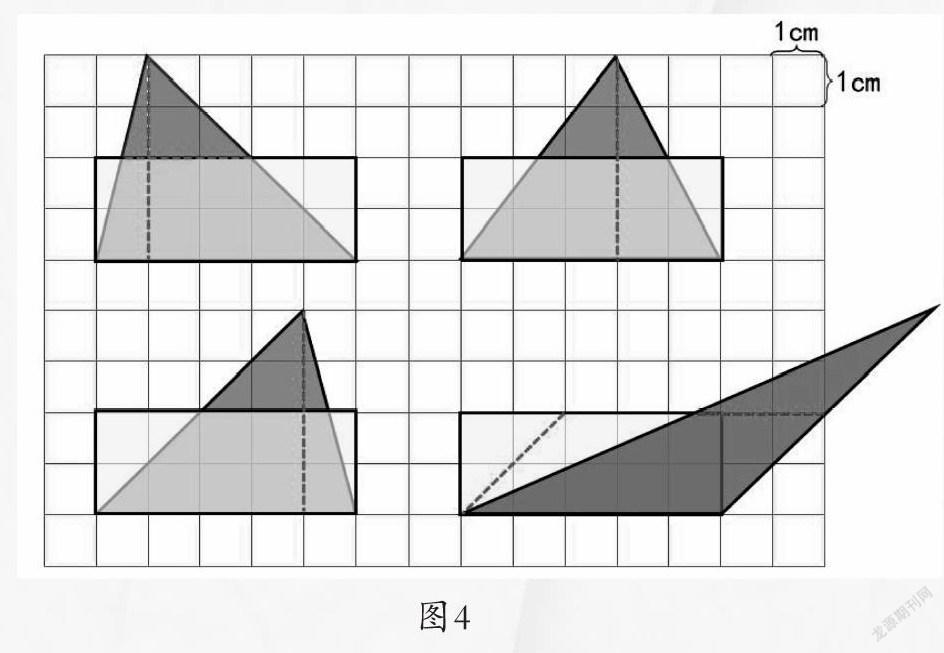
因此，如何帮助学生在面对此类问题的时候，让一些理论上早就“明确”的结果看起来更加真实，就显得特别有价值了。教材中也介绍了我国古代数学家刘辉的“出入相补”思想（如图3），这就为帮助学生把“等底等高的三角形面积相等”这一数学命题可视化提供了强大的支撑。实验下来，效果特别好（如图4）。

这一回，再也没有人怀疑“等底等高的三角形面积相等”这一个数学结论了——因为它们通过“出入相补”转化以后，全部变成了一模一样的长方形！

启示：

1.数学知识的呈現形态要多样化。学生在数学思维方面的个体差异是比较明显的：有的学生喜欢数理分析，有的学生喜欢直觉形象，有的学生喜欢做中学，有的学生喜欢辩中思……面对个性鲜明的学生，数学知识不应该像模子里刻出来的机器零件一样千篇一律，而是应该在保持本质不变的情况下穿上不同的“外衣”，以适应不同学生对数学学习的个性化需求。

2.数学知识的学习要结构化。数学知识逻辑严密，系统性强。学会了结构化思维，数学知识就会越学越“少”。通过“出入相补”对三角形进行转化，再结合其他图形的类似操作，很多学生都明白了平面图形面积计算的本质——用面积单位去度量图形。在不方便度量的时候，就想办法把不规则的平面图形转化得尽量规则，并最终归结为“每行的面积单位个数×行数”这一根本方法上。