面向飞行器交会对接应用的载波相位差分技术研究

陈万通， 李小强

(1.中国民航大学 智能信号与图像处理重点实验室，天津 300300；2.北京航空航天大学 电子信息工程学院,北京 100191)

面向飞行器交会对接应用的载波相位差分技术研究

陈万通1， 李小强2

(1.中国民航大学 智能信号与图像处理重点实验室，天津 300300；2.北京航空航天大学 电子信息工程学院,北京 100191)

GNSS引导两飞行器交会对接的前提是实时可靠地估计相位模糊度。针对卫星和飞行器的高动态性所引发的频繁换星问题，提出一种实时递归相位模糊度估计方法。该算法能够有效处理失锁所造成的卫星起落现象，同时充分利用历史观测与当前观测方程中部分模糊度分量的关联性，使得模糊度估计的成功率对可见卫星数目的减少不敏感。为了验证该算法在空间飞行器对接中的精度和成功率,采用GPS模拟器仿真两飞行器近程导引段和最终逼近段的过程，应用新算法实时估计两飞行器间相对位置，精度达到亚厘米级水平，成功率在可见星数递减时依然渐进逼近100%。

全球导航定位系统；相对定位；递归最小二乘；成功率；相位模糊度

0 引 言

空间飞行器交会对接需要实时高精度地确定两飞行器的相对位置，应用GNSS 载波相位差分技术引导两飞行器交会对接，是近年来国内外关注的一个重要方向[1]。理论上，精密的载波相位观测值可以实现静态相对定位精度毫米级精度水平，动态相对定位亚厘米级精度水平。由于载波是一种周期性的正弦信号，进行相位测量时存在着观测信号的整周模糊度问题，这正是载波相位测量的技术难点。因此，实时可靠解算相位模糊度是GNSS相对定位技术的关键[2]。

与大地测量学不同的是，应用GNSS进行空间飞行器精密相对定位面临该应用所具有的特殊问题，星载GNSS 接收机是在高速运动状态下进行信号接收，历元间极易发生卫星跟踪中断现象，从而引起频繁的卫星“升起”和“落下”现象，导航处理器必须能够在实时递归处理过程有效地处理这部分观测数据[3]，另外动态测量中要求模型强度随着时间推移具有不断增强的可靠性，避免出现因实时解算的可靠性不足导致观测中断[4]，同时相对定位所采用的数学建模模型要求具有数据异常的检测能力，能够自动检测到系统故障[5]。针对上述三种问题，本文提出一种面向飞行器交会对接应用的实时递归估计方法，解决了高动态情况下可见卫星数目对模型递归过程和成功率的影响。

1 基本数学模型

假定交会对接的两个飞行器分别定义为A和B，A和B之间的相对位置为基线矢量b，GNSS引导两飞行器交会对接目标即是精确估计基线矢量b。为了实现该目标，需要建立载波相位观测值与基线矢量之间的数学模型。

首先，对于同一卫星i，其单差载波相位观测方程[6]表述如下:

(1)

(2)

基线矢量的中点到卫星的站星矢量为

(3)

令ei为其单位化矢量，则有

(4)

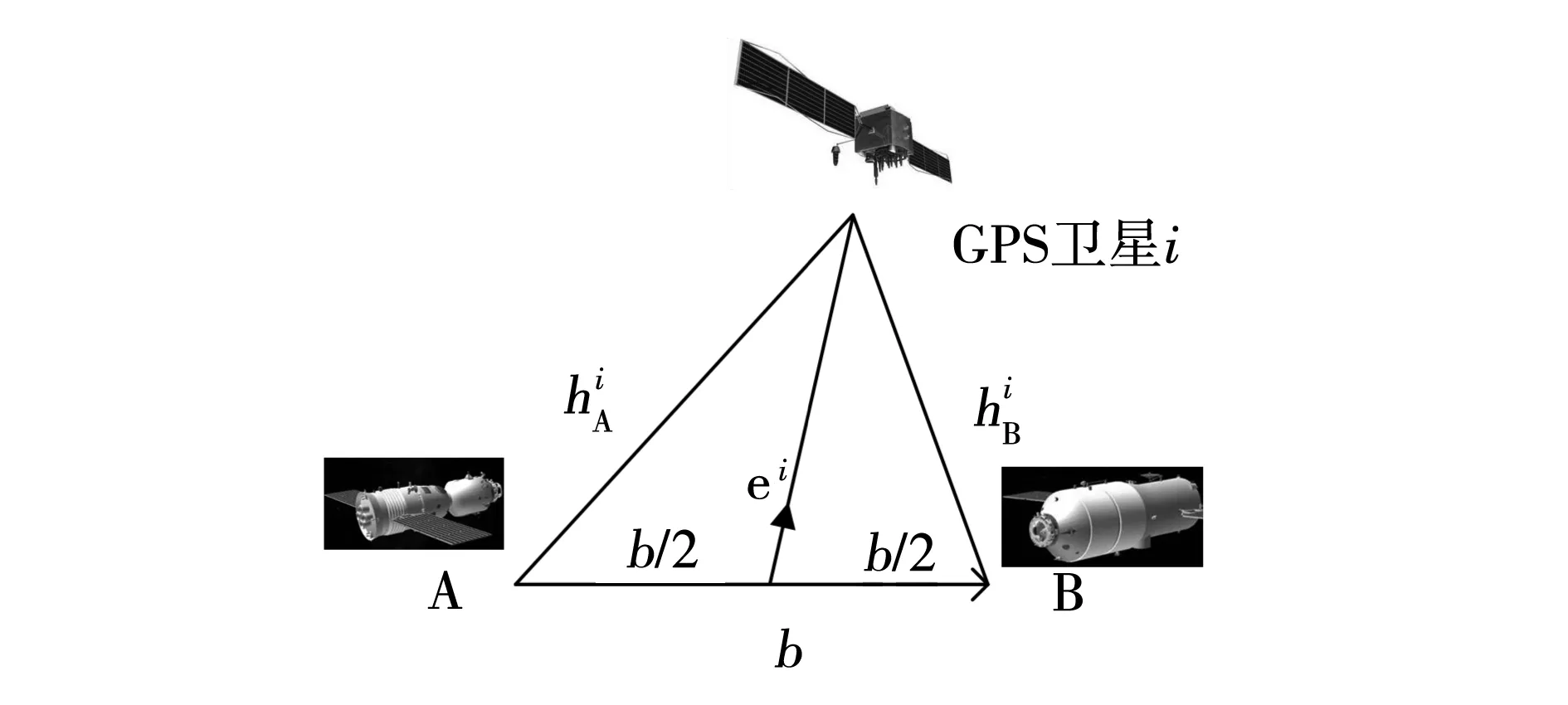
图1 交会对接飞行器与卫星差分示意图Fig.1 Satellite differential schematic of spacecraft rendezvous and docking

(5)

则单差站星距与基线存在如下数学关系

(6)

令ei的系数为

(7)

(8)

类似方法可得不含模糊度的码双差方程：

(9)

2 递归参数估计算法

对于任意短基线，假定第k个历元的卫星可见数mk大于4颗并且ωiei已获得，则其双差载波/码联合观测方程可以统一成如下形式的标准数学模型[2]：

yk=Akak+Bkbk+vk,vk～N(0,Qyk)
ak∈Zmk-1,bk∈R3。

(10)

其中:y表示双差载波和双差码的联合观测矢量，维度为2mk-2；a为整周模糊度矢量，其维度为mk-1；b为当地地理坐标系下的基线矢量，包含东北天三个分量；A和B分别为a和b的系数设计矩阵，维度分别为(2mk-2)×(mk-1)和(2mk-2)×3；v为y的观测噪声矢量；Qy为其方差协方差矩阵。下标k表示所有观测向量和矩阵均属于第k个历元。由于观测量y通过双差方法得到，故各分量存在较强的互相关，即Qy为非对角阵，为了实现观测量的去相关，对Qy采用Cholesky分解，即

Qyk=Lk(Lk)T。

(11)

构造矩阵Xk=(Lk)-1，式(10)两边同时乘以该构造矩阵，则得到

(12)

其中

(13)

(14)

其中Qk为正交矩阵，其维度为(2mk-2)，Rk为上三角阵，其维度为3。令

(15)

令式(15)作用于式(13)的两边可得

(16)

即原来的方程可以视作两个部分，第一个包含基线坐标和双差模糊度，即

(17)

另一个只包含双差整周模糊度，即

(18)

由于正交变换不改变观测噪声的统计特性，所以标准正态分布依然保持

(19)

(20)

其中Sk是m-1阶上三角阵。令

(21)

(22)

(23)

正交变换不改变噪声的统计特性，则

(24)

式(19)中ak为整数向量，首先求得k历元整周模糊度的浮点估计值

(25)

(26)

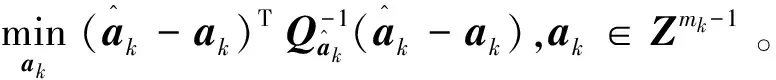
(27)

求得整周模糊度，就可以代入式(17)求得基线向量b。一般而言，为了提高整周模糊度解算的成功率，通常采用多个历元的观测进行联合估计，然而，在高动态环境中，常会出现某时刻卫星信号由于失锁对于接收机“不可见”，而当卫星位置变动时，又会有新的卫星被捕获和跟踪，即面临卫星频繁变换的问题。事实上，失去锁定的卫星，其在失锁之前的观测方程和现在仍然在跟踪的卫星之间依然存在部分模糊度分量的关联，利用这部分“历史”观测信息，必然能够增加整周模糊度解算的信息量，提高可靠性。采用同样的方法，我们在k+1历元得到和式(18)类似的表达式

(28)

假定在k+1历元参考星仍然保持连续跟踪，相比k历元的观测，部分非参考星在k+1历元仍然被连续跟踪，并且假设有新的卫星被跟踪，则ak+1的各个分量可以重新调整为

(29)

为了实现上述模糊度分量的次序调整，构造如下置换矩阵：

(30)

(31)

等价替换可得

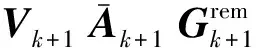
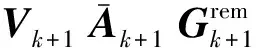
(32)

将上式代入式(28)可得

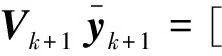
(33)

为了实现k历元和k+1历元的联合估计，构造另外一组置换矩阵Πk+1，调整上一历元的模糊度次序：

(34)

使得

(35)

(36)

将式(36)代入式(23)可得

(37)

那么联合式(33)和式(37)可得

(38)

再次构造正交矩阵Pk+1，使得

(39)

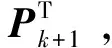
(40)

(41)

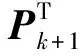
(42)

令上部Ck+1与Sk+1的维数相同，则可进一步提取式(40)的上部得到

(43)

其中

(44)

注意到式(43)依然是上三角系统，并且与k历元的递归结果具有同样的形式，故可以采用相同的计算方法获得k+1历元对整周模糊度及其方差协方差矩阵的估计，分别如下：

(45)

(46)

上述过程中假设参考星不发生失锁，对于参考星变换，可以采用置换矩阵对式(43)进行等价变换。双差整周模糊度采用的是以第1颗星为参考星，即

(47)

当第1颗星卫星因运动而不是仰角最高的时候，需要变换参考星，当第i(i>1)颗星为参考星，则双差整周模糊度为

(48)

(49)

其中置换矩阵K的第i-1列元素为-1，其余对角线元素为1，即

(50)

若式(23)中的ak以第1颗星为参考星，则应用换星算法之后有

(51)

后续历元可继续应用非参考星换星算法进行处理。

3 成功率与可靠性

整周模糊度解算的成功率通常用模糊度精度因子(ambiguitydilutionofprecision,ADOP)来计算[9]，即来衡量，其计算方法如下：

(52)

成功率计算公式如下：

(53)

其中n为模糊度的维数，Φ(·)为累计正态分布函数，定义如下：

(54)

≡[Hhis|Hcur]。

(55)

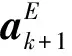
(56)

图2 全局/局部整周模糊度估计成功率对比Fig.2 Success rate comparison of global/local integer ambiguity estimation

当模型中存在周跳、粗差或异常数据，可视作如下假设检验：

(57)

(58)

(59)

拒绝H0假设，即认为数据和H1假设更匹配，模型误差具体识别方法可参见文献[5]。

4 仿真实验

为了验证上述方法的有效性，利用中国空间技术研究院提供的交会对接模拟数据进行实验，仿真数据利用GPS模拟器产生。针对交会对接过程近程导引段和最终逼近段进行仿真，两个飞行器之间的距离从4 400米到对接停靠阶段之前的约18米，持续时间为3652个历元，历元间隔为1秒钟。

由于GPS卫星和航天器之间的相对速度和相对加速度均较大，持续跟踪的卫星数目波动较为频繁，整个仿真过程中可见星数目在7-11颗之间波动，图3给出了此次实验的可见星数目，使用本文所提递归算法处理卫星起落现象，将扩维后的总体模糊度维数以及全局成功率估计结果一并呈现在图3中，可通过观察发现：即使卫星数目在观测中逐渐递减至7颗，全局成功率依然渐进逼近于1，对卫星数目的骤减不敏感。其本质原因为递归模型充分利用了历史观测与当前观测方程中部分模糊度分量的关联性，使得在动态测量中模型强度随着时间推移具有不断增强的可靠性。

图4为解算的飞行器之间的相对距离，也即基线长度，从4 400m逐渐递减至18m左右，与GPS模拟器预设的仿真动态过程相符。图3和图4中蓝色竖线代表初始化完成的分界线，初始化过程仅仅历时167个观测历元即实现Ratio检验值超过2，初始化完成时间较短。

通过对比模拟器仿真此次交会对接实验的真实值，图5给出了估计值与真值之间的误差，在解算的初始阶段，误差约1～2cm，约300个历元之后误差收敛至1cm之内，从而验证了模型的有效性，该精度满足近程导引段和最终逼近段的需求。

图3 可见星数目与全局成功率Fig.3 Visible satellite number and global success rate

图4 近程导引段和最终逼近段的相对距离估计值Fig.4 Estimated relative distance of short range guidance phase and the final approach phase

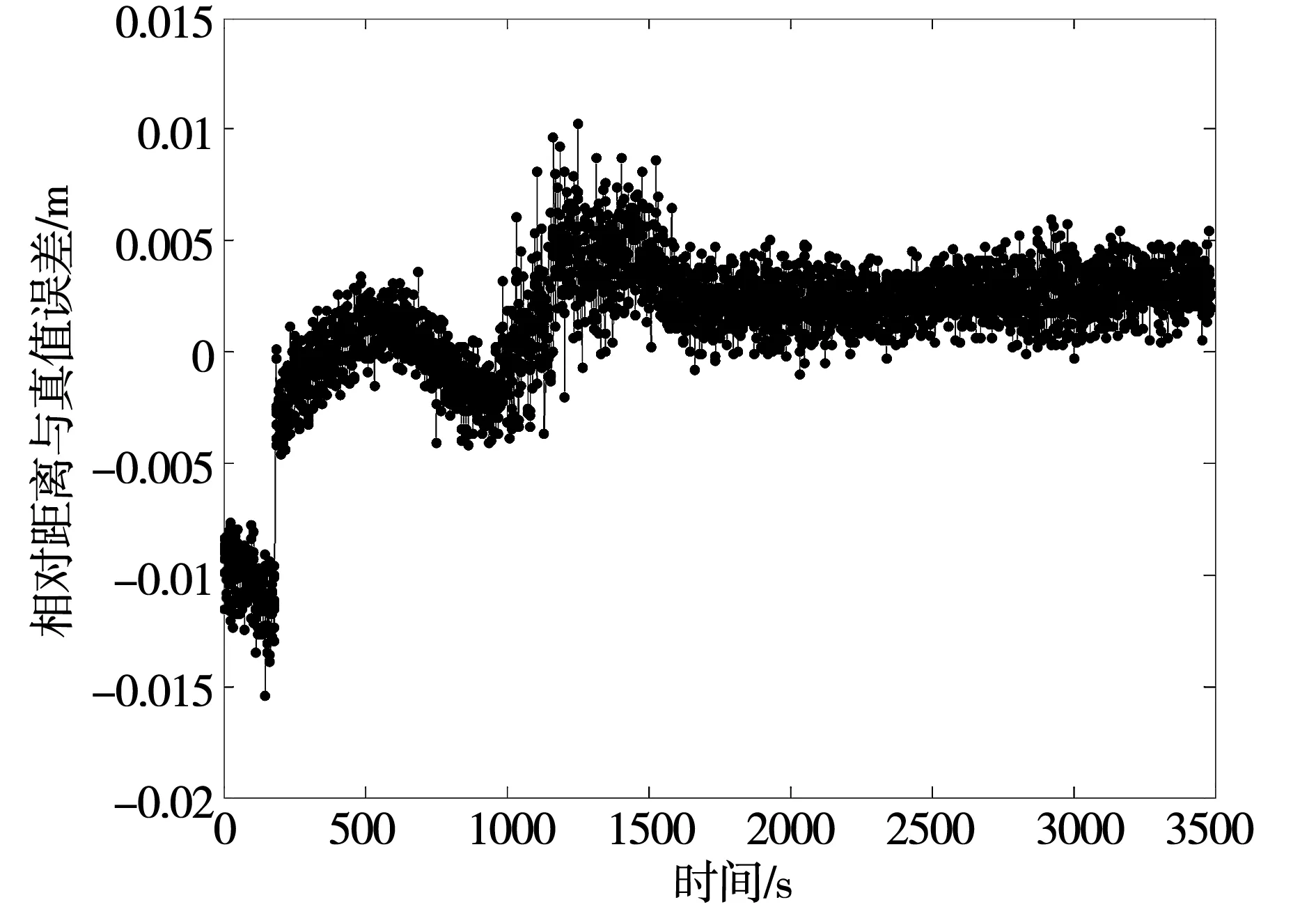
图5 相对距离估计值与真值之间的误差Fig.5 Error between the estimated value and the true value

5 结 论

与大地测量学应用不同，面向空间飞行器交会对接应用的GNSS相对定位技术面临更多挑战。高动态导致的可见星频繁更替使得经典基线模型无法直接使用，且卫星数目的减少使算法成功率急剧降低。本文提出一种换星扩维算法，能够有效地处理递归解算中的卫星更替，同时充分利用历史观测与当前观测方程中部分模糊度分量的关联性，扩展了整周模糊度估计的维度，提高了成功率，对可见星数目短时间内的减少不敏感，其可靠性和解算精度满足飞行器交会对接应用，也可促进GNSS在航空飞行器编队飞行等相关领域的应用。

[1] 阳仁贵,袁运斌,欧吉坤.相位实时差分技术应用于飞行器交会对接研究[J].中国科学: 物理学 力学 天文学,2010,40(5): 651-657. YANG Rengui,YUAN Yunbin,OU Jikun.Real-time GNSS carrier phase differential technique for spacecraft rendezvous and docking[J].SCIENCE CHINA Physics,Mechanics & Astronomy,2010,40(5):651-657.

[2] Buist P J,Teunissen P J G,Giorgi G,Verhagen S.Multivariate bootstrapped relative positioning of spacecraft using GPS L1/Galileo E1 signals[J].Advances in Space Research,2010,47(5):770-785.

[3] CHEN Pei,SHU Leizheng,DING Ran,et al.Kin-ematic single-frequency relative positioning for LEO formation flying mission[J].GPS Solutions,2015,19(3):525-535.

[4] Mohiuddin S,Psiaki M L.High-altitude satellite relative navigation using carrier-phase differential global positioning system techniques[J].J Guidance Control Dynamic,2007,30(5):1427-1436.

[5] 陈万通，秦红磊，丛丽，等.GPS姿态测量中的可靠性理论GPS姿态测量中的可靠性理论[J].电机与控制学报，2010,14(8): 63-69. CHEN Wantong,QIN Honglei,CONG Li,et al.Research on reliability in attitude determination with GPS[J].Electric Machines and Control,2010,14(8): 63-69.

[6] Montenbruck O,Wermuth M,Kahle R.GPS based relative navigation for the TanDEM-X mission-first flight results[J].Navig J Ins,2011,58(4): 293- 304.

[7] CHANG X W,Paige C C,YIN L.Code and carrier phase based short baseline GPS positioning: Computational aspects[J].GPS Solutions,2004,7(4): 230-240,2004.

[8] CHEN W,LI X.Success rate improvement of single epoch integer least-squares estimator for the GNS-S attitude/short baseline applications with common clock scheme[J].Acta Geodaetica et Geophysica,2014,49(3): 295-312.

[9] Teunissen P J G.GNSS ambiguity resolution[J]. Journal of Geodesy,2004,78(1):235-244.

[10] CHEN Wantong,QIN Honglei.New method for single epoch,single frequency land vehicle attitude determination using low-end GPS receiver[J].GPS Solutions,2012,16(3):329-338.

(编辑：张 楠)

Research on GNSS carrier phase differential technique for spacecraft rendezvous and docking

CHEN Wan-tong1， LI Xiao-qiang2

(1.Tianjin Key Lab for Advanced Signal Processing,Civil Aviation University of China,Tianjin 300300,China;2.School of Electronic and Information Engineering,Beihang University,Beijing 100191,China)

The premise of guiding two aircrafts with GNSS is the real-time and reliable estimation of phase ambiguity.To deal with the frequent satellite setting and rising caused by high dynamic movement of satellite and aircraft,one new method was presented for real-time and recursive phase ambiguity estimation.It handles frequent satellite setting and rising due to loss of lock.Also,by utilizing the ambiguity relevance of past observation and current observation,the success rate of integer ambiguity estimation is not sensitive to the number of satellite setting and rising.In order to verify the accuracy and the success rate of this algorithm in the application of the spacecraft rendezvous and docking,based on GPS simulator,the rendezvous and docking was simulated for short range guidance phase and the final approach phase of two aircraft.Then the new algorithm was applied to estimate the relative position between the two aircrafts using the simulation data,and it shows that the relative position precision achieves the sub-centimeter level and the success rate was still gradually approaching 100% when the number of visible satellites decreased progressively.

GNSS；relative positioning；recursive least squares; success rate；phase ambiguity

2015-09-26

国家自然科学基金(61401468)

陈万通(1986—)，男，博士，讲师，研究方向为卫星导航、相对定位与姿态测量； 李小强(1985—)，男，硕士，讲师，研究方向为卫星导航、机载设备自动测试系统以及GNSS RTK技术。

陈万通

10.15938/j.emc.2017.03.015

V 249.3

A

1007-449X(2017)03-0104-07