带有输入时延的刚性航天器反最优姿态控制

毕显婷， 史小平

(哈尔滨工业大学 控制与仿真中心，黑龙江 哈尔滨150080)

带有输入时延的刚性航天器反最优姿态控制

毕显婷， 史小平

(哈尔滨工业大学 控制与仿真中心，黑龙江 哈尔滨150080)

针对带有输入时延的刚性航天器提出一种姿态稳定性控制方法，首先利用反步法构造李雅普诺夫控制函数，由此得到使系统全局渐近稳定的时延补偿控制器。由于航天器系统为强耦合非线性系统，基于反最优理论，对非线性时延系统构造关于系统状态量和控制力矩的目标函数，该目标函数体现了能耗的重要性，并得到相应的最优控制器。将无优化指标考虑的控制器与最优控制器进行性能比较，非最优控制器所需能量消耗较大，仿真中给出了定量分析结果。仿真结果显示，不同时延情况下，该控制器均可以有效控制航天器姿态稳定，并且对于时延估计偏差具有鲁棒性。

时延；反步法；反最优；全局渐近稳定

0 引 言

航天器姿态控制系统主要包括敏感器、控制器和执行器，其中敏感器和执行器都会引入时延。例如，星敏感器中姿态估计算法消耗的时间一般为1～10 s[1]；推力器在执行过程中，受电磁阀开启时延的影响[2]。姿态敏感器和推力器的动态时延会降低航天器性能，引起航天器的振颤和抖动现象[3]，严重情况下甚至导致系统失稳。本文对具有执行器时延的刚性航天器进行姿态稳定控制器设计。

航天器作为强耦合非线性系统，时延的引入导致模型从非线性常微分方程变成非线性时延微分方程，确定系统每一时刻的状态所需初始条件从初始值扩展到初始函数。已有文献设计的姿态稳定控制器主要包括两类：基于构造完全型Lyapunov-Krasovskii(L-K)泛函方法设计线性常增益状态反馈控制器；基于补偿思想的非线性状态反馈控制器。

为了分析线性时延系统的稳定性，文献[4]提出了一种构造二次型L-K泛函的方法，由于该L-K泛函中包含了系统过去时刻的状态，因此可以用于分析时延参数不确定时系统的稳定性，即具有时延鲁棒性。在此基础上，文献[5]将该方法扩展到非线性系统，以执行器带有时间延迟的航天器模型为背景，采用修正罗德里格斯参数集(modified rodrigues parameter set,MRPs)对航天器建模，以避免在非线性项中出现时延，进而将其视为干扰，设计了使系统姿态稳定的线性状态反馈控制律，稳定性在吸引域内成立。文献[6]继续对此方法进行改进，利用线性矩阵不等式获得控制器增益系数，进一步减小了收敛域的保守性。文献[7]将时延下限信息用于构造L-K泛函，文献[8]在L-K泛函中增加三重积分项，文献[9]应用保守性更小的不等式，文献[3]设计了无需姿态角速度信息的状态反馈控制器。上述研究思路的优点是控制器容易实现，但只能达到局部稳定，并且对吸引域和时延上限的估计比较保守，系统稳定性条件受时延上限和状态初值限制。

为达到全局稳定性，需要设计非线性控制器，反步法是较为常见的控制方法。文献[10-11]为将反步法应用在非线性时延系统提供了理论基础，分析了非线性时延系统在具有时延补偿的反步控制器作用下的稳定性。文献[12]将此方法应用到受输入时延影响的刚性航天器姿态稳定控制，设计了具有全局稳定性的控制器。该文献中提到了控制器的最优性质，但所满足的最优指标只是系统状态的函数，并未体现对控制力矩的约束。

本文研究具有输入时延的刚性航天器的最优控制问题。由于Hamilton-Jacobi方程较难求解，本文应用反最优理论，设计全局稳定的最优反馈控制器。首先，基于MRPs建立系统模型，利用反步法设计李雅普诺夫函数并得到具有全局稳定性的反馈控制器，然后构造目标函数，最终得到最优指标意义下的最优控制器。

1 系统建模

1.1系统运动学模型及虚拟控制律设计

对于刚性航天器，其运动学方程可以用MRPs表示为

(2)

(3)

将式(1)中的ω(t)视为输入，控制σbi(t)从初始值收敛到姿态原点，设计所需姿态角速度轨迹ωd(t)为

ωd(t)=-kσbi(t)。

(4)

其中k>0。

构造李雅普诺夫候选函数v(σbi(t))，有

v(σbi(t))=2ln(1+σbi(t)2)≥0。

(5)

其关于状态轨迹(1)导数为

(6)

根据李雅普诺夫稳定性理论知，在虚拟输入(4)的作用下，系统(1)全局渐近稳定。

1.2 系统动力学模型

执行器输入受时延情况下，不考虑外部噪声干扰，航天器动力学模型为：

(7)

u(φ)=0,φ∈[-τ,0]。

(8)

其中：J∈3×3是刚体的惯量矩阵；u(t-τ)∈3为时延后的控制输入，τ∈(0,τmax]为时延量；ω×(t)∈3×3为ω(t)的斜对称矩阵。

定义误差姿态角速度ωr(t)≜ω(t)-ωd(t)，系统闭环模型表示成：

(9)

(10)

u(φ)=0,φ∈[-τ,0]。

(11)

2 反最优控制器设计

引理1[13]考虑系统

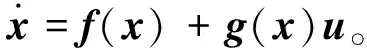
(12)

其中x∈n为系统状态向量，u∈m为控制输入，f:n→n和g:n→n×m为平滑函数。

如果存在如下形式的反馈控制律u使得系统(12)稳定，有

(13)

其中R:n→n×n为对称正定矩阵。

则有控制律

u=κ*(x):=βκ(x),β≥2。

(14)

对于目标函数J最优

(15)

其中

(16)

定理1对于目标函数

(17)

其中

(18)

其最优控制律为

(19)

证明：

对t≥τ时的闭环系统(9)和系统(10)构造李雅普诺夫泛函

(20)

其导数为

(21)

由于：

(22)

(23)

将式(22)和式(23)带入式(21)得到

(24)

由于

(25)

带入式(24)并进行整理，得到

(26)

取

(27)

方程(26)可重新写为

(28)

因此当控制律为式(29)时，系统稳定，有

(29)

根据引理1可知，当目标函数为

(30)

其中

(31)

最优控制律为

(32)

与最优二次型问题相一致。因此，本文所构造目标函数具有明确的物理意义。

证毕。

3 仿真分析

取航天器转动惯量J=diag[1 000,500,700]kg·m2，姿态角初值σbi(0)=[-0.2;-0.1;0.2]，姿态角速度初值ω0=[0.01;-0.02;0.02]，时延1s,k=0.1，应用反最优控制器(32)进行仿真。由于MRPs不具有物理意义，为便于理解，按照3-2-1转序将姿态参数从MRPs转化成欧拉角形式。仿真结果如图1所示。

从图1可以看出，在执行器引入1 s时延情况下，航天器在本文所设计的控制律作用下，姿态角和姿态角速度在200 s内达到稳定。

为说明本文所设计控制器的最优性质，下面与无优化指标考虑的控制器性能进行比较。同样利用反步法，一种使闭环系统(9)和系统(10)达到渐近稳定的直接时延补偿控制器为

u(t-τ)=ω×Jω-k1Jωr(t)-

(33)

取k1=0.2;k2=0.1;k3=0.1。在相同初始条件下，非最优控制器(33)所得到的仿真结果如图2所示。

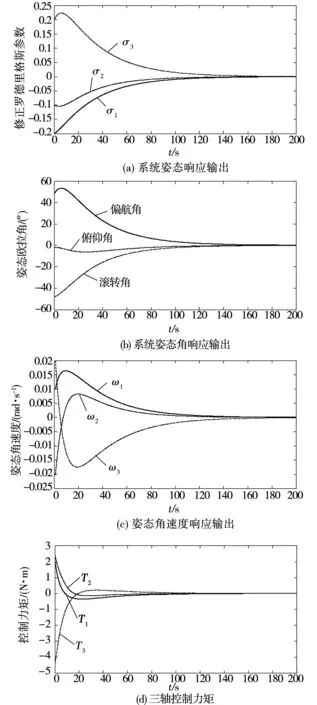
图1 时延1 s时，系统状态轨迹Fig.1 System state trajectories,τ=1 s

与图1相比，非最优控制器系统虽然可以保证状态渐近稳定，但控制力矩的峰值大于反最优控制器。为对两者进行定量分析比较，下面定义能量函数为

(34)

通过对该函数的计算比较两种控制器能量消耗上的差异。仿真结果如图3所示。

图2 时延1 s时，非最优控制器的系统状态轨迹Fig.2 System state trajectories with non-optimal controller,τ=1 s

从图3可以看到，航天器姿态达到稳定时，反最优控制器的能量消耗为100，而非最优控制器能量消耗为2 300，两者差异显著。

下面给出存在输入长时延情况下，系统的状态曲线。当执行器引入10s时延时，系统其它参数不变，进行仿真。仿真结果如图4所示。

图3 能量函数比较Fig.3 Energy function comparison

图4 时延10 s时，系统状态轨迹Fig.4 System state trajectories,τ=10 s

图4显示，时延10s情况下，系统状态轨迹仍然渐近收敛，与图1对比，所需控制力矩变大。

考虑到实际应用中，标称时延和时延真值之间存在偏差，对此情况进行仿真。设置系统标称时延0.8s，时延真值1s，仿真结果如图5所示。

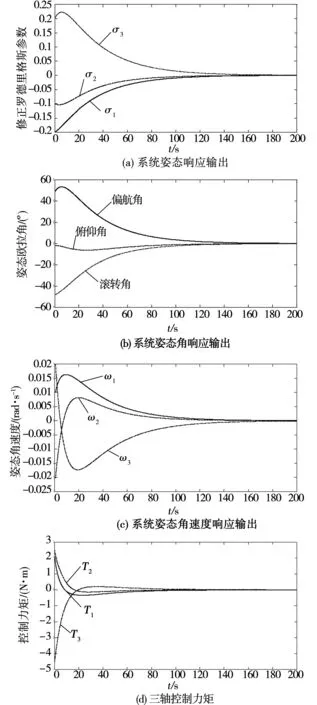
图5 实际时延0.8 s，估计时延1 s时，系统状态轨迹Fig.5 System state trajectories,τ=0.8 s with 0.2 s deviation

图5的结果表明，在存在时延参数估计偏差的情况下，状态量仍然能够很好的收敛，并且状态轨迹和控制力矩曲线与图1相比，并没有明显的变化，这说明本文所设计的控制律具有一定的鲁棒性。

4 结 论

本文对带有执行器时延的刚性航天器进行姿态稳定性控制，利用反步法得到具有全局稳定性的时延补偿控制器，根据反最优理论，构造关于系统状态和控制力矩的目标函数，得到最优控制器。仿真结果分别验证了在存在执行器短时延、长时延以及时延参数偏差等情况下反最优控制器的有效性和对时延参数的鲁棒性，利用能量函数对能量消耗的定量分析也表明了反最优控制器的优越性。

[1] BAHRAMI S,NAMVAR M.Rigid body attitude control with delayed attitude measurement[J].IEEE Transactions on Control Systems Technology,2015,23(5): 1961-1968.

[2] 屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社,2001:426-427.

[3] AILON A,SEGEV R,AROGETI S.A simple velocity-free controller for attitude regulation of a spacecraft with delayed feedback[J].IEEE Transactions on Automatic Control,2004,49(1):125-130.

[4] KHARITONOV V L,ZHABKO A P.Lyapunov-Krasovskii approach to the robust stability analysis of time-delay systems[J].Automatica,2003,39(1): 15-20.

[5] CHUNODKAR A A,AKELLA M R.Attitude stabilization with unknown bounded delay in feedback control implementation[J].Journal of Guidance,Control,and Dynamics,2011,34(2): 533-542.

[6] SAMIEI E,BUTCHER E A.Suboptimal delayed feedback attitude stabilization of rigid spacecraft with stochastic input torques and unknown time-varying delays[C]//In AAS/AIAA Astrodynamics Specialist Conference,2013,Hilton Head Island,SC，USA.2013:13-837.

[7] SHAO H Y.New delay-dependent stability criteria for systems with intervaldelay[J].Automatica,2009,45(3):744-749.

[8] SUN J,LIU G P,CHEN J,et al.Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J].Automatica,2010,46(2): 466-470.

[9] EMHARUETHAI C,NIAMSUP P.H∞ control for nonlinear systems with time-varying delay using matrix-based quadratic quadratic convex approach[J].Mathematical Problems in Engineering,2015: 1-12.

[10] KRSTIC M.Delay compensation for nonlinear,adaptive,and PED systems[M].Boston: Birkhauser,2009:153-169.

[11] MAZENC F,BLIMAN P A.Backstepping design for time-delay nonlinear systems[J].IEEE Trans.Autom.Control,2006,51(1): 149-154.

[12] SAFA A,BARADARANNIA M,KHARRATI H,et al.Global attitude stabilization of rigid spacecraft with unknown input delay[J].Nonlinear Dynamics,2015,82(4): 1623-1640.

[13] KRSTIC M,TSIOTRAS P.Inverse optimal stabilization of a rigid spacecraft[J].IEEE Trans.Autom.Control,1999,44(5): 1042-1049.

(编辑：刘琳琳)

Inverse optimal stabilization of rigid spacecraft in presence of input delay

BI Xian-ting， SHI Xiao-ping

(Control and Simulation Center,Harbin Institute of Technology,Harbin 150080,China)

An attitude stabilization controller of the rigid spacecraft in the presence of input delay was proposed.Firstly,a Lyapunov function was constructed after backstepping transformation of the original spacecraft model,and a time delay compensated controller that can guarantee global asymptotic stability was obtained.Considering the strong coupling nonlinearity of spacecraft system,the inverse optimal theory was then utilized to construct a cost functional with penalty on both system states and control torque,which reflects the importance of energy cost,and the optimal controller was consequently obtained.Compared with the optimal controller,the controller without optimal consideration costs more energy,quantitative analysis was given in simulation.Simulation results show the proposed controller is effective on attitude stabilization with different time delay,moreover,it is robust with delay uncertainty.

time-delay; backstepping; inverse optimal; global asymptotic stability

2016-04-10

国家自然科学基金(61074127)

毕显婷(1988—)，女，博士，研究方向为非线性时延系统、航天器智能控制； 史小平(1965—)，男，教授，博士生导师，研究方向为飞行器智能控制、复杂系统仿真。

毕显婷

10.15938/j.emc.2017.03.012

TP 13

A

1007-449X(2017)03-0083-06