附加历元间约束的滑动窗单频实时精密单点定位算法
2022-05-31杨凯淳吕志平李林阳邝英才
杨凯淳,吕志平,2,李林阳,3,邝英才,许 炜,郑 茜
1. 信息工程大学地理空间信息学院,河南 郑州 450001; 2. 哈尔滨工业大学(深圳)空间科学与应用技术研究院,广东 深圳 518055; 3. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,湖北 武汉 430077; 4. 西安科技大学测绘科学与技术学院,陕西 西安 710054
单频接收机由于价格低廉、操作方便,已广泛应用于变形监测、低轨卫星定轨及地面网解算等领域[1-3],然而单频精密单点定位(precise point positioning,PPP)的定位精度与多频PPP相比,还存在一定差距,最大的难点在于电离层延迟的改正[4-6]。不少学者对其开展了很多研究,得到了有效的处理方法[7-9]。
目前,主要采取以下4种方法改正单频PPP的电离层延迟:①采用电离层模型,但利用GPS导航电文中的Klobuchar模型,只能消除50%~60%的电离层延迟,而IGS格网数据精度为2 TECU,在电离层活跃及IGS站很少的区域其精度更低[9-10];②构成半合观测值,该方法只消除了电离层延迟的一阶项,且由于模糊度与接收机钟差高度相关,无法获得真实的钟差估值[11-12];③将电离层斜延迟作为未知参数估计[13-16],目前普遍采用的是文献[13]中的三参数法,同时估计对天顶延迟、水平梯度、映射函数,但模型过于简单,无法较好地描述电离层的活动,特别是在电离层延迟剧烈变化的区域;④通过多频接收机建立区域电离层模型,对单频接收机进行改正[17-18],该方法在距离较远且条件不好时,不方便使用。若不使用电离层模型也不拟合电离层斜延迟,而是直接将其作为参数求解,不仅可以获取高精度的电离层延迟信息与测站坐标,还能在一定程度上提高收敛速度[14,19]。
单历元单频PPP算法在同时解算电离层延迟时会出现秩亏问题[11,15,19],而使用多历元联合求解足以克服这一难题,本文提出了一种附加历元间约束的滑动窗算法(简称多历元递推单频PPP算法)。该方法无须额外的电离层延迟先验信息与模型,直接将各卫星斜路径上的电离层延迟作为参数估计,降低了电离层延迟对定位精度的影响。另外,本文采用附加约束的平方根信息滤波(square root information filter,SRIF)进行解算,可以充分利用多历元递推过程中各个参数的时间相关性建立内部约束,提高定位精度和收敛速度。
1 单历元单频精密单点定位算法
参数合并后的单频PPP模型为
(1)

除了三参数法[13]和附加约束的单频PPP算法[14],还可以添加模糊度约束[15]。文献[15]提出了同时估计电离层延迟的方法,将式(1)的未知参数分为两类
(2)

(3)
式中,k表示第k历元。
可将观测方程写为
Lk=Hy,kyk+Hg,kgk+vk,vk~N(0,Qk)
(4)
式中,Qk为对角阵;Hg,k和Hy,k是对应未知向量gk和yk的偏导数矩阵。
该方法通过参数约化减少解算时间,但定位精度仍受限于约束方程的准确性。
2 多历元单频定位模型及解算方法
相对于用模型改正电离层延迟,直接对电离层延迟进行估计定位精度更高。约束条件中,先验信息的准确性及约束建立的客观性都会导致精度下降及收敛时间的增加。多频非差非组合PPP对电离层延迟的处理方式分为3种:①仅通过电离层模型对其进行修复[20];②直接将电离层斜延迟作为参数进行估计[21];③添加电离层延迟约束,并对电离层斜延迟进行参数估计[22]。
方法①与方法③已在单频PPP中得到应用,但秩亏导致无法直接采用方法②。在多频非差非组合PPP中,方法③通过添加电离层延迟约束,分离硬件延迟与电离层延迟参数,定位精度比方法①与方法②更高,而单频PPP中电离层延迟参数只含有卫星端硬件延迟,可通过DCB(differential code biases)文件进行改正,不添加电离层延迟约束就达到较高的定位精度,避免外部先验约束的影响。
对于方法②造成的秩亏问题,假设可用卫星数为n,则单历元观测的方程个数为2×n个,待定参数包括三维坐标、接收机钟差、对流层天顶湿延迟、n个站星斜径分量电离层延迟以及n个模糊度参数,总共5+2×n个参数,秩亏数为5。此时,可通过联合多个历元的观测值,在解决秩亏问题的同时不引入额外的误差。
2.1 观测方程
假定有m个历元,n颗卫星,线性化后的多历元单频PPP模型可表示为
(5)
滑动窗内的观测方程可简化为
Y=Ax+ε
(6)
(7)
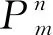
未发生周跳时,整周模糊度数值不变,因此,在多历元联合解算时,每颗卫星只需解算一个模糊度参数,此时通过联合多个历元,即可得到唯一解。假设有n颗卫星,联合m个历元,则共有2×n×m个观测值,静态情况下,需要估计3个坐标参数、1个对流层湿延迟参数、m个钟差参数、n×m个电离层参数及n个模糊度参数,待求参数有4+m+n×m+n个,其自由度为n×m-1)-m-4;动态情况下有4×m+1+n×m+n个参数,自由度为n×(m-1)-4×m-1。此时,除坐标参数需要估计3×m个以外,其余参数设置均与静态情况相同。
若静、动态情况下解唯一,则可用卫星数与联合的历元数需要满足的条件为
(8)
式中,nstatic为静态情况下的可用卫星数;nkinematic为动态情况下的可用卫星数;INT(·)为取整函数。
由式(8)可知,当联合的历元数增加,所需卫星数在逐渐变少。考虑到计算效率及计算精度,本文选择联合5个历元观测值进行计算,此时静态情况下至少需要3颗卫星,动态情况下至少需要6颗卫星。
2.2 随机模型
利用卫星高度角和观测值噪声来确定伪距和载波观测值的权,其中σP=0.1 m,σφ=0.001 m。
另外,本文采用多历元的解算模式,可以考虑历元间观测值的相关性,并将其体现在方差-协方差矩阵中,此时该矩阵不再是对角阵,表示如下
(9)
式中,QYmYm为第m个历元观测值之间的方差-协方差阵;QY1Ym指第1个历元的观测值与第m个历元观测值之间的方差-协方差阵。
自相关系数法可以描述不同历元观测值之间的时间相关性[23],本文通过自相关系数法来确定不同历元间观测值的方差-协方差阵。该方法定义如下
ρτ=ρij=ρjiτ=|i-j| (i,j=1,2,…,m)
(10)
因此,自相关函数中元素的自相关系数可以导出为
(11)
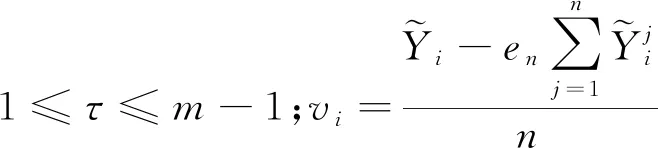
对于参数的随机模型,静态情况下,坐标固定且先验约束为100 m,动态情况下,坐标采用白噪声模型且先验约束也为100 m;接收机钟差采用白噪声模型;对流层干延迟采用Saastamoinen模型改正,其湿延迟采用随机游走模型估计;电离层延迟采用随机游走模型;模糊度当作常数处理,且为了克服接收机钟差、电离层延迟和相位模糊度之间高度相关导致的列秩亏问题(秩亏数为1),选择第1个滑动窗的第1组模糊度作为S基准,并将其约束到近似值,该近似值通过单频的相位观测值减去伪距观测值得到[24-25]。
对于不同历元间参数的先验方差-协方差阵,不同测站确定的先验方差-协方差阵不同,这里以SHAO站DOY 91的观测数据为例,首先通过同时估计电离层单频PPP算法100个历元的计算结果,确定相邻历元间钟差及电离层参数的相关系数,结果见表1、表2;然后根据其确定多历元递推单频PPP算法的先验方差-协方差阵。
表1中,i=1,2,…,5;cDt 1表示第1个历元的钟差参数,Iono 1表示第1个历元的电离层延迟参数。由于本文方法在静态定位解算时,只有电离层延迟与钟差参数需要每个历元都设置1个,因此,表1和表2中只给出了这两个参数的相关关系。经反复试验后发现,在动态定位中也同样需要考虑钟差与电离层延迟参数在历元间的相关性。
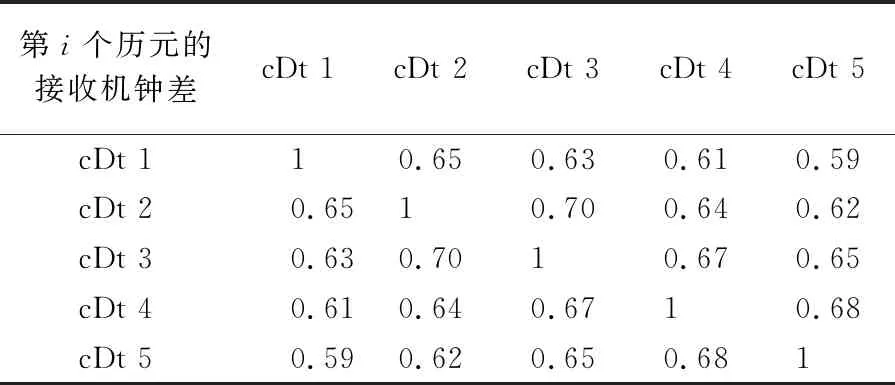
表1 历元间钟差的相关系数
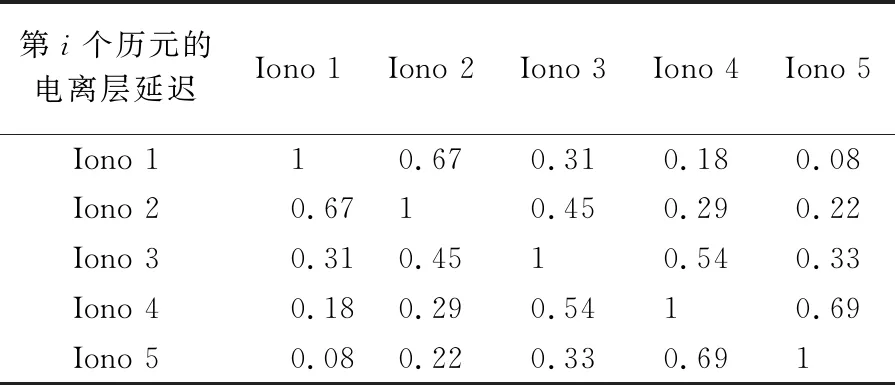
表2 历元间电离层延迟的相关系数
由表1和表2可知,不同历元间钟差之间的相关系数基本保持在0.6以上。而反观电离层延迟,仅仅在相邻历元间相关系数大于0.6,其余历元间的相关系数都较低,Iono 1与Iono 3之间的相关系数为0.31,Iono 1分别与Iono 4和Iono 5之间的相关系数都低于0.2,可认为相关性较弱。相邻历元间的电离层延迟之间以及接收机钟差之间的相关性都较大,而不相邻历元间的电离层延迟相关性较小,接收机钟差相关性仍较大。根据以上分析,本文方法必须考虑不同历元间的电离层以及钟差的相关性,并体现在参数的方差-协方差阵中。
在确定先验方差-协方差阵后,进行多历元递推单频PPP的解算,图1给出了不同历元间各个钟差及电离层延迟参数之间的相关系数。将图1与表1、表2进行对比,可以看出多历元单频PPP比单历元单频PPP参数之间的时间相关性要强,在进行多历元联合解算的过程中必须要考虑。
2.3 参数估计方法
多历元联合解算通常使用最小二乘法,而批处理十分占内存,不满足动态实时系统状态估计的需求。为了充分利用之前的解算结果,本文提出一种多历元递推与SRIF算法相结合的方法,建立滑动窗口,滑动窗口的大小等于联合解算的历元数,每次解算时,将其往下滑动一个历元,直到最后一个历元完成解算。由于在相邻的两次解算结果中,部分参数是等价的,此时可以通过这个等价关系添加历元间的参数约束,提高解算精度、增加解的稳定性。
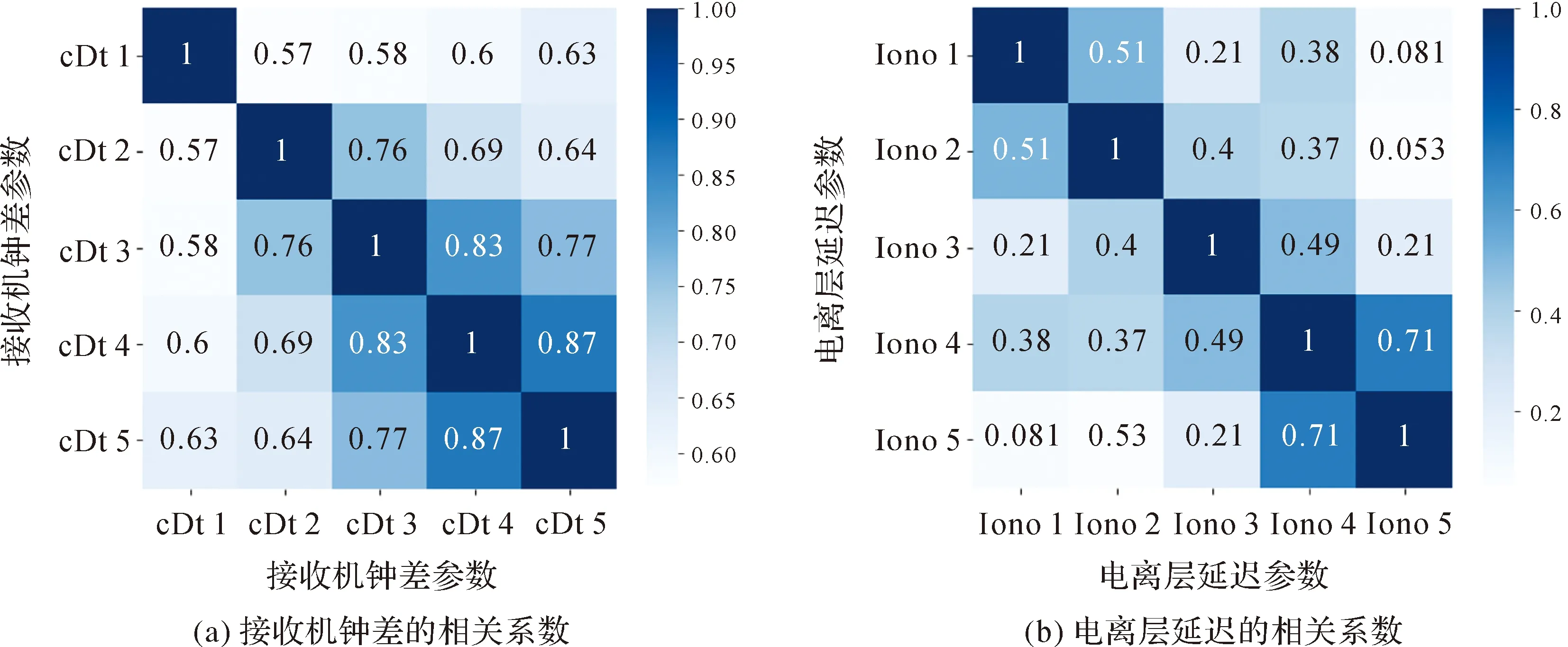
图1 历元间电离层延迟与接收机钟差的相关系数Fig.1 Correlation coefficient of ionospheric delay and receiver clock correction between epochs
将观测方程式(6)中的参数按被约束与不被约束分组,写成误差方程形式
V=Ba+Cd-l
(12)
式中,a为不被约束的m个历元的参数;d为被约束的参数;B与C分别为a与d的系数行满秩矩阵;l为误差向量。
约束条件方程写为
Dd-E=0
(13)
考虑到计算效率以及计算结果的精度,预先对不同约束组合进行试验,并根据试验结果分别在动静态情况下对各参数进行不同的约束,见表3。
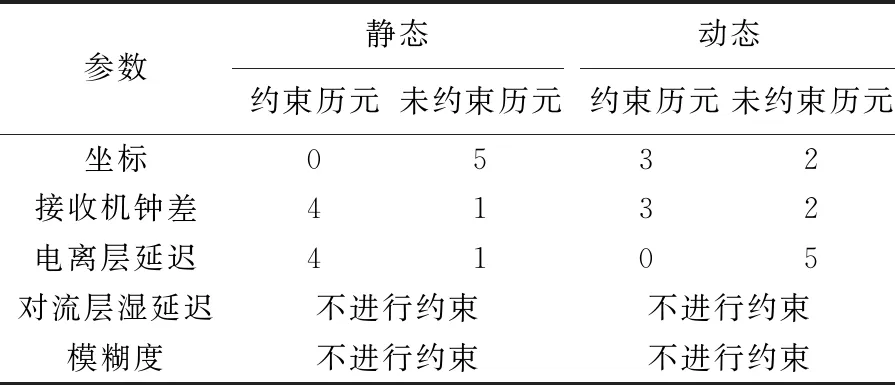
表3 各参数约束情况
表3共联合了5个历元的观测值,静态情况下只对接收机钟差与电离层延迟进行约束,接收机钟差与电离层延迟的约束历元数都为4个,分别表示对前4个历元的接收机钟差与电离层延迟进行约束;动态情况下只对坐标与接收机钟差进行约束,其约束历元数都为3个。
图2给出了本文算法的流程,分为如下4步。
(1) 预处理,通过多普勒积分法与相位伪距组合法探测并修复周跳[26],利用数据探测法探测并修复粗差,探测与修复钟跳,并剔除卫星数据不好的时段。
(2) 联合预处理后的多历元观测信息,建立观测方程并将其线性化。
(3) 根据自相关系数法确定观测值之间的方差-协方差阵,通过同时估计电离层单频PPP算法100个历元的计算结果确定参数的先验方差-协方差阵。
(4) 进行参数解算,选择第1个滑动窗的第一组模糊度作为S基准,并使用带约束的SRIF算法进行解算。
3 试验分析
试验选取全球范围内的15个IGS站,采用2019年3月19日(DOY 78)至2019年4月1日(DOY 91)共14 d,采样间隔为30 s的观测数据,分别进行动静态PPP测试分析,图3为所选的测站分布图。以下分别将各方法的PPP解算结果与参考真值做差,获得E、N、U 3个分量上的坐标偏差,以分析同时估计电离层延迟的单频PPP、双频无电离层PPP及多历元递推单频PPP算法的收敛时间和定位精度。本文中的滤波收敛定义为E、N、U各向定位偏差均优于10 cm。为确保结果的可靠性,同时检查首次收敛时刻后续20个历元的位置偏差,只有当连续20个历元的偏差都在限值以内时,才认为滤波在当前历元收敛[27]。
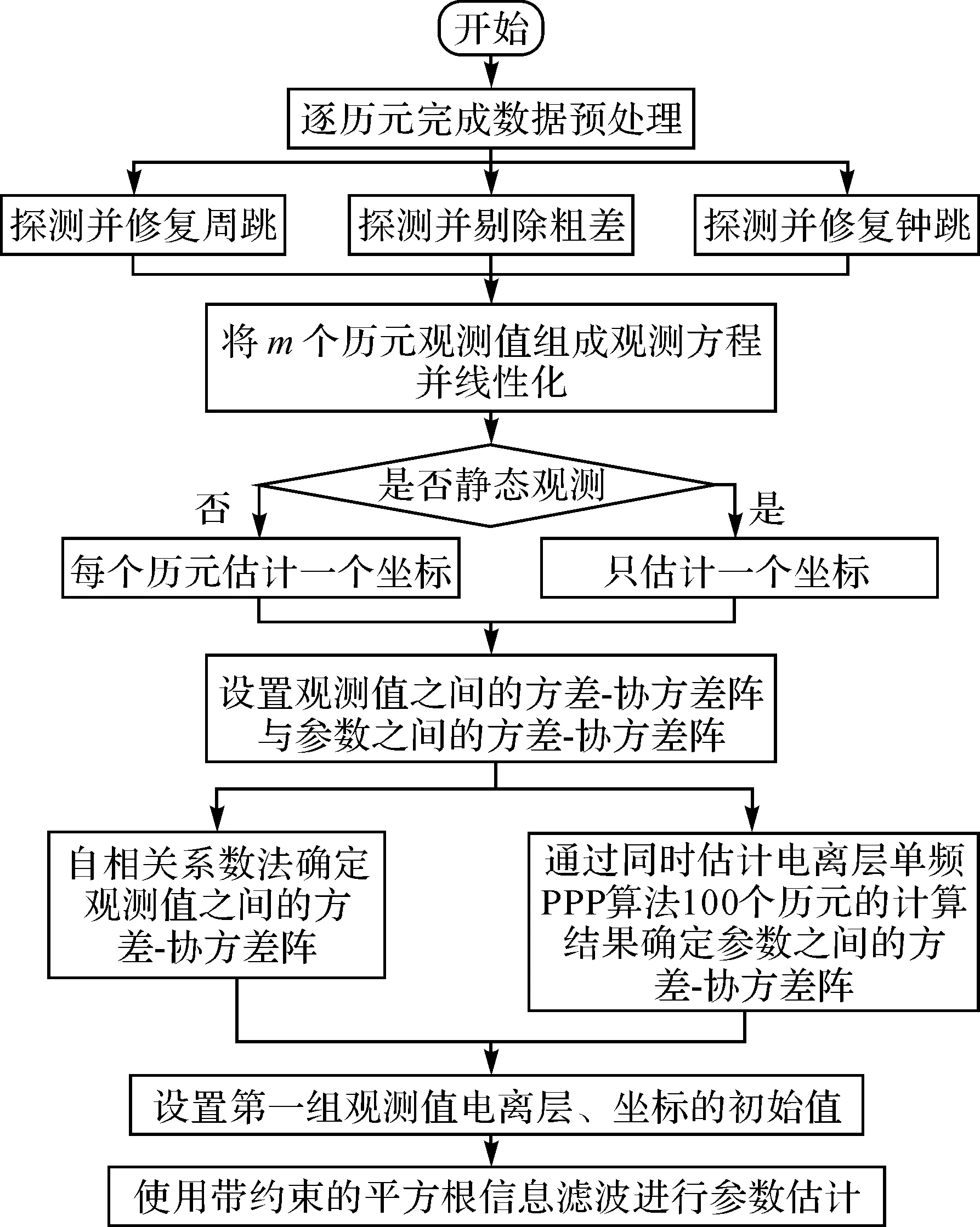
图2 多历元递推单频PPP算法流程Fig.2 The flow chart of multi-epoch recursive single-frequency PPP algorithm
图3 测站分布Fig.3 Stations distribution
3.1 静态定位
本文通过对5个历元的观测数据进行联合解算得到如图4所示的结果。
图4为多历元算法与单历元算法在单天内的PDOP值及可用卫星数的变化。在多数情况下,多历元比单历元的可用卫星数多且卫星几何分布更好,但由于多历元算法对数据质量要求较高,需要剔除数据质量不好的卫星,在部分历元,多历元算法反而比单历元算法的PDOP值低且可见卫星数少。另外,对未经预处理的原始数据进行试验,发现多历元递推算法更易受到周跳及粗差的影响。
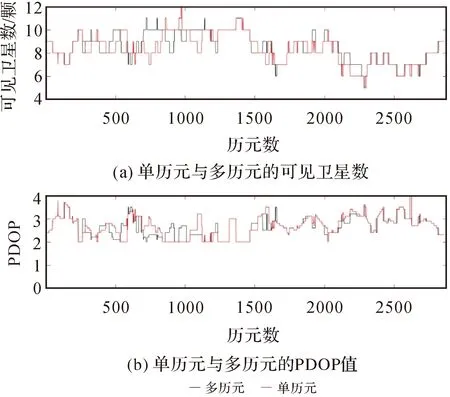
图4 多历元与单历元算法的PDOP值及可见卫星数对比Fig.4 Comparison of PDOP value and visible satellites between multi-epoch and single-epoch algorithm
经过以上分析可知,多历元算法比单历元算法更好。使用传统的间接平差对多历元联合算法进行数据处理,可以得到图5中的定位结果。由图5可知,定位结果较差,E分量最大达到了1 m,N分量在0.5 m左右波动,U分量大部分在1 m左右波动。根据2.3节的分析可知,间接平差只处理当前存储的数据,并没有充分利用上一次解算的结果,若当前解算的m个历元的数据质量较差就会导致偏差很大,在U分量上更为明显。
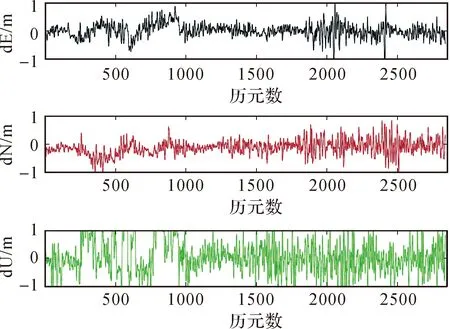
图5 SHAO站多历元联合的单频PPP(间接平差)Fig.5 SHAO station single-frequency PPP based on multi-epoch (indirect adjustment)
采用本文算法,设置方案(a)、方案(b)、方案(c) 3种处理方案,分别为同时估计电离层延迟的单频PPP,多历元递推单频PPP(平方根信息滤波)以及双频无电离层PPP,处理得到3种方案下SHAO站的静态定位精度,如图6所示。相比同时估计电离层的单频PPP算法,多历元递推单频PPP算法在3个分量的精度更高,特别是在高程分量,且该方法与双频无电离层PPP的定位精度基本相同。
对比图6(b)与图5可知,相比使用间接平差的多历元联合单频PPP算法,采用多历元递推单频PPP算法拥有更高的定位精度,水平分量的精度能够达到厘米级,且在高程分量上有较大改善。
剔除部分存在跳变的历元,综合15个测站14 d的定位结果,统计了静态定位的RMS、STD及平均收敛历元数,见表4。方案(b)中多历元递推算法的E、N和U分量上的RMS分别为0.017、0.008和0.028 m,优于方案(a)。方案(b)的收敛时间大大缩短,与方案(c)双频无电离层PPP的收敛速度基本保持一致。
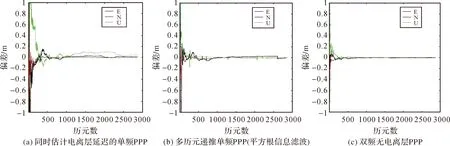
图6 3种方案下SHAO站的静态定位精度Fig.6 Static positioning accuracy of SHAO station under three different schemes
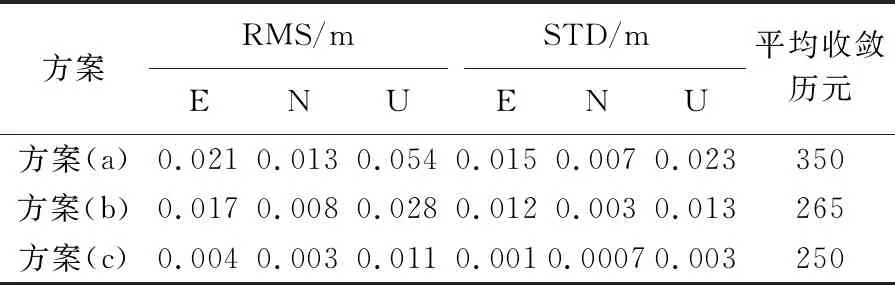
表4 静态定位平均RMS、STD和收敛时间
图7统计了SHAO站多天及所有站DOY 91的静态定位精度。由图7(a)可知,除U分量波动较大外,其余分量的RMS基本没有变化。E分量的RMS在0.015 m左右浮动;N分量的RMS略小于E分量,基本在0.005 m左右;U分量的RMS比E和N分量大,大约为0.025 m,但最大也仅为0.032 m。图7(b)中,水平分量的变化不大,E分量的RMS优于0.02 m,只有BAKO站超过了0.02 m,这是因为BAKO站在赤道附近电离层运动活跃,影响了定位精度;N分量整体优于0.015 m,且大多数测站不超过0.01 m;U分量的RMS结果相比E与N分量略差,仅有CONZ站的高程精度达到0.07 m,是由于该测站离海边较近,海潮改正的精度较差从而影响了其高程精度,但其余测站的RMS都优于0.08 m。整体来看,N分量定位精度均优于E分量,这是由于单频PPP只能使用浮点解,不能将模糊度固定为整数。
3.2 动态定位
采用方案(a)、方案(b)分别为同时估计电离层延迟的单频PPP,多历元递推单频PPP(平方根信息滤波),对多站多天的数据进行模拟动态定位试验,表5统计了平均RMS。

表5 两种方案下动态定位平均RMS
对比表5与表4中动静态RMS结果可知,动态情况下两种方法精度的差别更为明显,其原因是静态结果统计是对各时段收敛后最后1个历元的定位偏差计算RMS,而动态结果统计是从各时段的收敛时刻开始对偏差序列计算RMS。
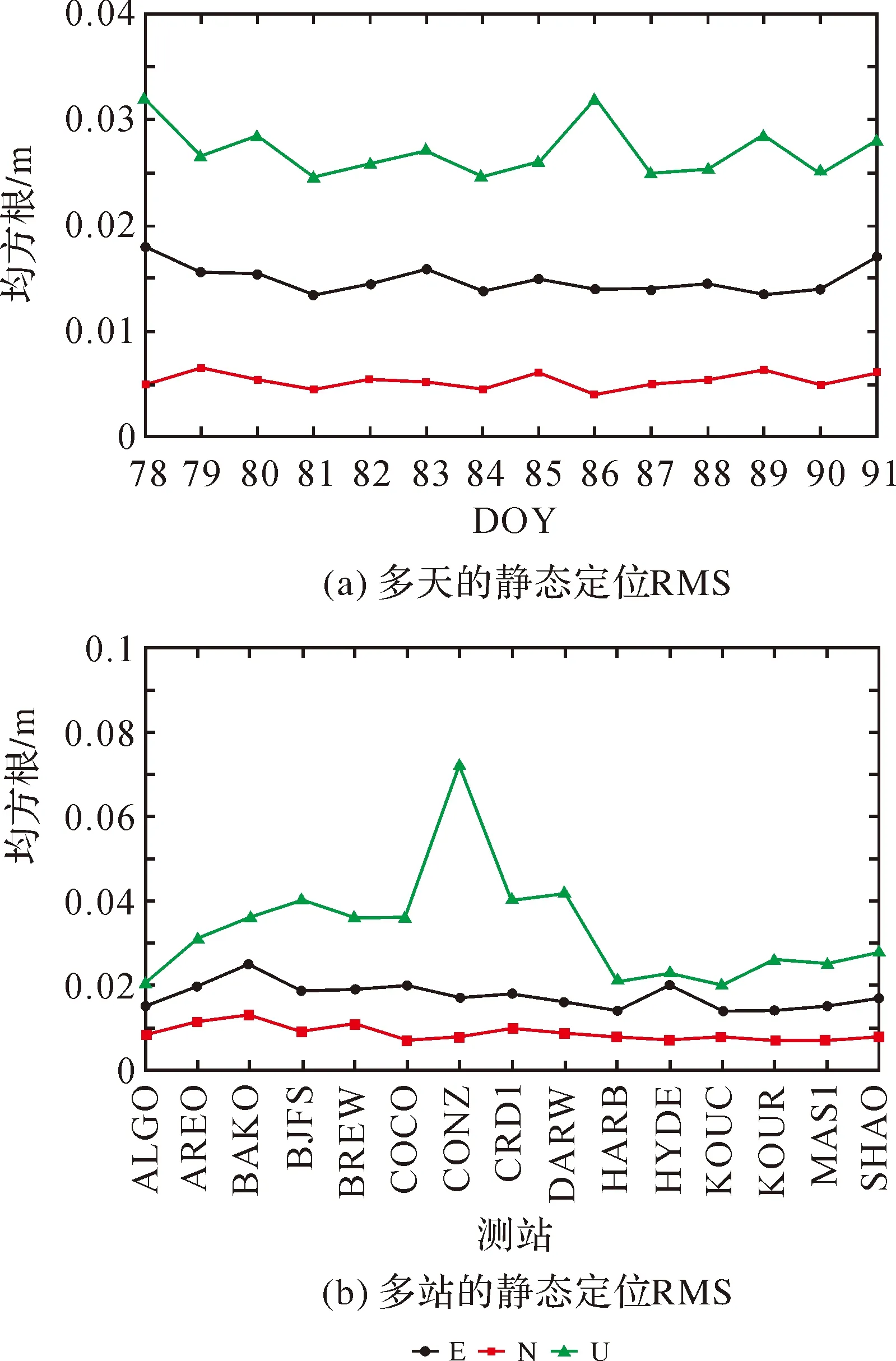
图7 多天及多站的静态定位RMSFig.7 Static positioning RMS for multi-days and multi-stations
图8给出了SHAO站多天定位及多站的动态定位精度。图8(a)中各天的变化较大,3个分量的变化量都达到了分米级,特别是在高程分量,其最大的RMS为0.16 m,最小的RMS约为0.12 m,该方法比双频无电离层PPP算法受到动态噪声的影响大,但比同时估计电离层的单频PPP算法受到的影响小。
图8(b)中,对于不同的IGS站,由于所在的纬度不同,电离层的活跃程度不同,使用多历元递推算法进行解算得到的平均RMS差别较大。其中CONZ站的高程精度达到了0.4 m,由于其位于海边,在动态情况下受到的海潮改正误差及观测噪声的影响更严重,导致其高程精度不理想。其余测站E、N和U分量上大部分分别优于0.15、0.12和0.23 m。
采用2011年10月26日7∶30—9∶30在德国莫里茨湖采集的船载观测数据进行试验,采样率为1 s,并与GNSSer软件的RTK固定解比较,图9给出了差值。
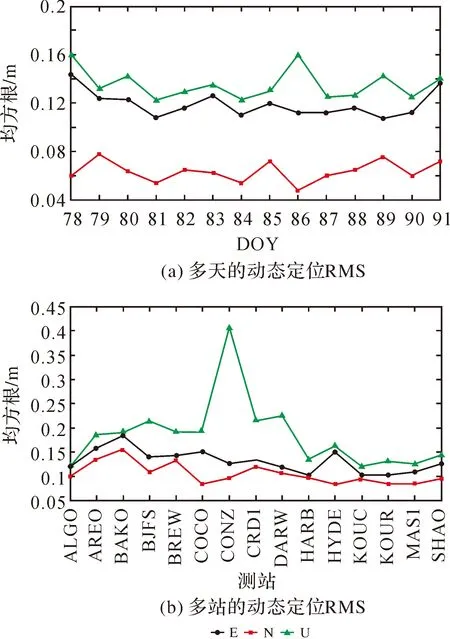
图8 多天及多站的动态定位RMSFig.8 Kinematic positioning RMS for multi-days and multi-stations
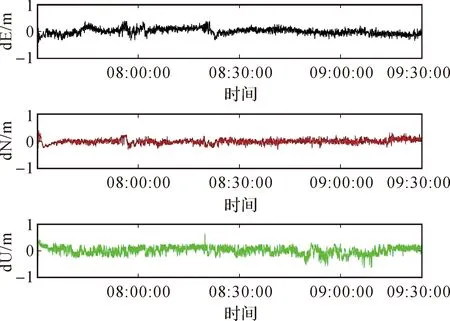
图9 船载观测数据的定位误差Fig.9 Positioning errors of Shipborne data
由图9可知,PPP算法的定位结果比RTK算法差,相比模拟动态试验,海上实测动态试验的定位偏差更大,但动态情况下误差在E和N分量上都不超过0.5 m,在U分量上不超过 0.7 m。
表6统计了船载数据动态定位的RMS和最大偏差,可以看出水平分量上的最大值为0.416 m,高程分量上的最大值超过了0.6 m,3个分量上的RMS不超过0.2 m,验证了本文方法在实测动态情况下的可靠性。

表6 动态定位的最大偏差和RMS
4 结 论
本文研究了一种联合多历元观测值数据进行解算的单频PPP算法,该算法不需要外部电离层延迟信息,也不需要对观测值进行组合或求差,通过多历元联合求解的方式解决了添加电离层延迟参数之后的秩亏问题,主要结论如下。
(1) 使用多历元联合解算,不需要对电离层进行建模,且能够在保留原始观测信息的同时,解算电离层延迟。另外,该算法还考虑了参数之间及观测值之间的相关关系,提高了收敛速度及定位精度和稳定性。
(2) 根据多历元递推观测方程的特殊性,通过一种带约束的SRIF算法,充分利用了相邻历元间参数的相关关系,提高解算精度,减少收敛时间。
(3) 采用多历元观测值联合求解,大大提高了可用卫星数,静态定位精度优于3 cm,仿动态解约为1.5 dm,相比同时估计电离层延迟的单频PPP方法,收敛速度提高了24%,甚至与双频无电离层PPP算法的收敛速度基本一致,定位精度提高了30%,尤其是高程分量定位精度提高更为明显。
