高效课堂,贵在“衔接”—初中与小学“数与代数”教学的衔接策略

广东省中山市东升镇旭日初级中学(528414) 张苏伟

高效课堂,贵在“衔接”—初中与小学“数与代数”教学的衔接策略

广东省中山市东升镇旭日初级中学(528414) 张苏伟

初中数学教师在教学中常常会发现一个现象,有不少在小学阶段数学成绩优秀的学生,在进入初一后却告别了昨日的“辉煌”,数学成绩出现比较大的滑坡,甚至有相当一部分学生丧失了对数学学习的兴趣和信心,数学成绩跌入谷底.究其原因,是因为小学和初中数学在教材内容、教师的教学方法和学生的学习方法上出现了严重的脱节,小学和初中数学教学的“衔接”迫在眉睫.为此,我们镇数学中心教研组开展了《义务教育阶段数学“数与代数”教学衔接研究》的市级立项课题研究.

相比小学,初中数学知识比较抽象且课堂容量较大,容易造成两极分化.初中数学教师只有重视小学与初中教学的有效衔接,找准教学切入点,才能打造出高效的初中数学课堂.我认为,要实现“有效衔接”,最关键在于“教学内容、符号语言和数学思想”三个方面的衔接.

一、教学内容,衔接之“源”

中小学数学教学的衔接,首先在于教学内容上的衔接,这是衔接之“源”.

《义务教育数学课程标准》明确规定了“数与代数”内容的主线是:从数及数的运算到代数式及其运算,再到方程和解方程、函数.

小学到初中的教学内容衔接主要体现在“从算术数到有理数的扩充”、“从数到式的过渡”和“从算术法到方程法解决实际问题的转变”三个方面.但是,小学教师不知道初中要具体学习的内容,难以为初中做好一些铺垫,而初中教师也因不了解小学教材而无法找准教学生长点,这就造成小学和初中数学的教学内容出现脱节.

针对教学内容的脱节问题,我们课题组成员潜心研读课标和中小学数学教材,花了整整一年的时间整理汇编出义务教育阶段数学在“数与代数”领域方面需要补充和完善的知识点和训练题集(如下图,简称为“小册子”),让全镇数学老师对中小学“数与代数”的教学目标和内容一目了然,并对中小学数学教师提出教学建议.比如,初中教师以前只知道近几年小学六年级已引入了“负数”,但不知道学生对“负数”的了解有多深.如今,通过小册子里中小学数学关于“负数”教学目标的对比,我们容易知道,学生在小学仅有对“负数”形式的一个基本感知,以及从熟悉的“温度高低”生活情境中初步体会两个负数的大小比较,这样,初中老师在教学“负数”时就有了立足点和侧重点.

这本小册子还在不断试验改进中,它凝聚着全体课题组成员的心血,是中小学数学教学内容有效衔接的桥梁.另外,课题组还创建了“东升镇中小学数学教师QQ群”,供老师们在教学内容衔接时进行实时沟通.这样,老师们就可以站在高处宏观把握中小学数学知识体系,让中小学“数与代数”教学内容的衔接问题迎刃而解.特别地,对初中数学“数与代数”的教学有着深远的意义.

图1

图2

二、符号语言,衔接之“本”

数学符号语言在数学学科发展中的地位举足轻重,它是唯一能够不分种族、国界进行数学交流的语言载体.人们通过数学符号语言体会数学奥妙、探讨数学方法、锻炼数学思维,使数学学科展现出了与众不同的独特魅力.初中数学从算术到代数的转变,导致处在思维过渡期的学生在符号语言学习过程中产生困难,这也成为了学生数学学习困难的一个重要因素.如何让小学习惯了直观形象思维的学生能逐渐掌握抽象逻辑思维为主的初中数学知识,这就离不开初中数学“符号意识”的培养.

《义务教育数学课程标准》也把“符号意识”作为数学学习内容的核心概念.《标准》指出,符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性;建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式.

而“符号意识”的培养,关键在于初中数学符号语言的教学和研究,此乃中小学数学教学的衔接之“本”.结合本人教学实践,我认为,初中教师在教学中要注重如下三个方面:

1.要注重在概念法则中的用“字母表示数”来培养学生的符号意识,让学生体会数学符号语言的概括美;

小学高年级学生已经知道,数的表示除了传统的数据还可以用字母符号表示,初中教师在新授课时要注意字母符号的引入,要善于挖掘符号信息,使学生认识到字母符号表示数、概念、法则和运算律的优势.比如,学生通过计算10+(−20)和(−20)+10的结果相同,再换几个加数计算仍相同总结出加法交换律,引导学生用字母a、b表示这两个加数,其中,a、b代表任意有理数,得出“加法交换律”的数学符号表示:a+b=b+a;同样探究出用字母表示各种运算律等.初一有理数的学习让学生充分体验到字母表示数的优越性,体会到数学符号语言的概括美.这样,符号意识就深深扎根于学生的思维中,对后续学习,比如对初二“平方差:(a+b)(a−b)=a2−b2”和“完全平方:(a±b)2=a2±2ab+b2”两个公式的理解也就水到渠成了.

2.要注重数学知识在“文字语言、符号语言和图表语言”三类形式之间的转化,让学生体会数学符号语言的简洁美;

例如,几乎所有学生都可以轻松求出|−5|=5,却有相当一部分学生对于“|x−3|+|y+1|=0,求x+y的值”此类题束手无策,归根到底是学生还未真正理解|a|的含义.因此,在“绝对值”概念教学中,我们应强调:数a的绝对值(文字语言),记作|a|(符号语言).而在数轴上来看,|a|表示数a的点到原点的距离,板书如下:

图3

借助数轴的表示,既然|a|表示“距离”,学生就容易理解|a|的非负性.

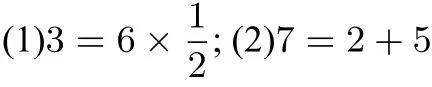
3是6的一半;(文字语言)

让学生仔细观察上面文字语言与下面数学符号语言之间的对等关系.有不少学生发现,文字语言中的“是”或“比”可以转化为数学符号“=”,“的”转化为“×”,“一半”转化为“”,而“大”则转化为“+”,类似地,“小”也就是“−”.

接着,出示层层递进的题目“请把下列语句‘翻译’成数学符号语言:(1)x比x的一半小7;(2)a的2倍比b的5倍大4;(3)x的80%是x与3的和的一半;(4)一个数的7倍比它的三分之二小6,设这个数为x.”有了刚才的铺垫,学生们都兴趣盎然地跃跃欲试,并慢慢体会到只要理解和记住了几个关键词的转化,复杂的文字语言就可以这么轻松地“翻译”成如此简洁的数学符号语言.

最后,过渡到“应用题”中的“调配问题”:甲班原来35人,乙班原来66人,问从乙班调多少人到甲班,才会使甲班人数比乙班的一半多20人?设从乙班调x人到甲班后,借助表格,学生容易得出甲班后来人数为(35+x)人,乙班后来人数为(66−x)人,再把“调配后甲班人数比乙班的一半多20人”这个等量关系“翻译”成数学符号语言:35+x=(66−x)+20,而这个符号语言也就是“方程”.我经常跟学生说,应用题很好玩的,只要找到了等量关系,就可以像英语里的“中译英”一样,把等量关系“翻译”成方程,“列方程”也就是“中译数”.通过这样循序渐进的引导,学生们都慢慢地爱上了应用题.

3.要注重从不同角度来解释同一个数学符号语言,构建符号语言知识网络,让学生体会数学符号语言的统一美;

初中数学很多知识点都有密切联系,需要加以整理才能让学生系统掌握和灵活运用.而各知识点联系的枢纽,正是数学符号语言.

又比如,数学符号“y=x−5”,从小学中“数的大小比较”角度来看,它表示“一个数比另一个数小5”;从初中“函数”角度来看,它是一个一次函数;从“方程”角度来看,它是一个二元一次方程;从“几何”角度来看,它是一条直线……这样,通过多个角度去解释同一个数学符号语言,能把函数、方程、几何等各板块的内容有机结合,帮学生构建符号语言知识网络.学生可以在该知识网络中自主探究发现“求直线y=kx+b(k0)与x轴或y轴的交点坐标”实质上也就是“代入求值”中“当y=0时,求x的值”或“当x=0时,求y的值”的问题.

初中符号语言,能引领学生从形象思维向抽象思维顺利过渡,是小学与初中数学教学衔接的根本.

三、数学思想,衔接之“魂”

有人说,数学思想是数学学习的灵魂.的确,如果把数学比作一条项链,那么珍珠就是数学知识,引线便是数学思想,而怎样用引线把数学知识串起来便是数学方法.没有数学思想方法,数学知识就如同一盘散沙!

从小学到初中的数学是一个从具体到抽象、从感性到理性的质的飞跃,而数学知识的学习关键在于数学思想方法的学习,它是建立知识学习与应用的桥梁.因此,我认为,数学思想方法的衔接,可以转变学生的思维方式,是中小学数学教学衔接的重要途径,可谓衔接之“魂”.

而所有数学思想方法中,最让人叹为观止的莫过于“数形结合思想”.比如,在探究“二次函数图像与x轴的交点个数与一元二次方程根的情况关系”中,以及“方程解实际问题”中的“分段收费”和“行程相遇或追及”等问题,我们教师若能渗透“数形结合法”,不仅使问题变得直观、生动、形象,还能把“数形结合”这一伟大的数学思想植根于学生的思维中,对终生学习有非常大的帮助.

总之,衔接是永恒的,探索是无尽的.只要我们初中数学教师从“教学内容”这一衔接的“源头”出发,致力于“符号语言教学研究”这个衔接的“根本”,紧扣住“数学思想方法”这个衔接的“灵魂”,就能打造出高效的初中数学课堂.

[1]中华人民共和国教育部,义务教育数学课程标准(2011版),北京师范大学出版社,2012年2月.

[2]叶文生,亟待关注的中小学数学教学衔接问题[J],中小学教学研究,2004,(4):11-12.

[3]李桂强,谈中学生数学符号感的培养[J],上海中学数学,2006,(7):15.