错在哪儿?—由一道中考错题想到的

北京师范大学出版集团(100875) 岳昌庆

错在哪儿?—由一道中考错题想到的

北京师范大学出版集团(100875) 岳昌庆

存在性问题一直是各级各类考试命题的重中之重的问题,能举出反例更是至关重要的,尤其是中考、高考等高利害性考试.请看2015年中考某市选择题的压轴题

例 1 已知抛物线 y=ax2+bx+c(a＞ 0)过(−2,0),(2,3)两点,那么抛物线的对称轴( ).

A.只能是x=−1

B.可能是y轴C.在y轴右侧且在直线x=2的左侧

D.在y轴左侧且在直线x=−2的右侧

由于第一大题(选择题)中明确指出“在每小题给出的四个选项中,只有一项是符合题目要求的”故选D.

错解2:因为函数图像经过(−2,0),(2,3)两点,所以由二次函数图像的对称性可知:函数图像与x轴的另一个交点在点(2,0)的左侧,所以抛物线的对称轴在y轴的左侧且在直线x=−2的右侧.故选D.

错因分析:错解1排除法不靠谱,默认前提:有且只有一个答案正确!

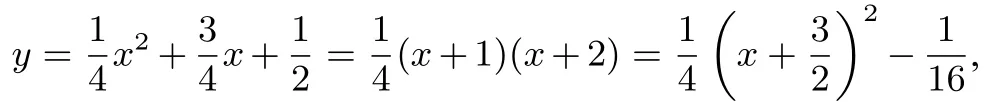
图1

图2

相信当时此题对考生影响不是太大,错解1及错解2均可“正确”选出答案D.可能心细的学生在此题上会多花一些时间,吃亏一些,略欠公允.

如何回避类似情况,以规避风险?

本着以人为本对考生负责的态度,建议中考命题专家组中,既要有初中一线教师、教研员,也要有高中一线教师、教研员,更要有大学教师把关.命题、审题、打印、校对、验算、保密等均是不可缺少的环节,甚至不排除小范围请教师、各级各类有代表性的学生试做.用《几何画板》验证其存在性、正确性等,切忌信手拈来、想当然.不能让崇高神圣的命题工作成为一种“意识流”.

另:各地教研机构、杂志、网络等勇于挑错、勇于正视瑕疵,将中考数学试题中的瑕疵曝于阳光下,以免一错再错,以讹传讹,继续贻误学子,损害高利害性考试的权威性与公信力.

例2[2015年中考四川省广元市卷第23题9分次压轴题][2012年中考湖北省恩施州卷第23题12分]如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.

图2

(1)求证:BC是⊙O的切线;

(2)连接AF,BF,求∠ABF的度数;

评注 一个错题不断流传之广,还能在3年后,又原封不动地作为另一个地区的中考压轴题.

例3[2015年中考广西南宁市卷第11题3分次压轴题]如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上一动点,若MN=1,则△PMN周长的最小值为( ).

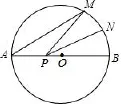
图4

A.4 B.5 C.6 D.7

所谓标准答案为B.

错因分析:“MN=1”是个富裕条件,且是个错误条件.实际上,考生可以算出MN=8sin10°≈8×0.1736≈1.39＞1,A.B.C.D.依次改为A.3+8sin10°,B.4+8sin10°,C.5+8sin10°,D.6+8sin10°.

例4[2014年中考四川省遂宁市卷第9题4分]如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )

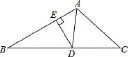
图5

A.3 B.4 C.6 D.5

所谓标准答案为A.

错因分析:若“AC=3”,过D作DF⊥AC于F,显然Rt△AEDRt△AFD,DF=DE=2,设AE=AF=x,则BE=4−x,CF =3−x,由角平分线定理得即7x2−24x+28=0,此方程无解.即符合已知条件的图是不存在的.

例 5[2014年中考湖北省随州市卷第9题3分]在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

图6

A.AE//BC B.∠ADE=∠BDC

C.△BDE是等边三角形 D.△ADE的周长是9

所谓标准答案为B.

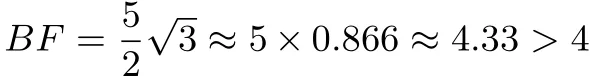
例6[2014年中考湖北荆门卷第6题3分]如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( ).

图7

A.∠ACD=∠DAB B.AD=DE

C.AD2=BD·CD D.AD·AB=AC·BD

所谓标准答案为D.

错因分析: 实际上A.B.C.D.全部正确,没有错误答案.可能是校对环节出了问题,只需将选项D中的“AD”改为“CD”即可.