2017年高三理科数学高考模拟卷

广东汕头聿怀中学(515041) 黄毓君 郑妍 李佩芳

2017年高三理科数学高考模拟卷

广东汕头聿怀中学(515041) 黄毓君 郑妍 李佩芳

一、选择题(共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案涂在答题卡相应的位置上)

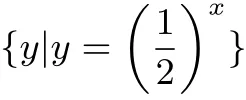
A.∅ B.(0,+∞)

C.(1,+∞) D.(−∞,0]

2.下列函数中既是偶函数又是周期为π的函数是∗

3.使“log2m＜1”成立的一个充分不必要条件是∗

B.m∈(−∞,2)

C.m∈(0,2) D.m∈(0,+∞)

4.为得到y=sin2x的图像,可将y=cos2x的图像∗

5.点B与点A(2,1)关于直线x−y+1对称,则直线AB与圆x2+(y−1)2=2的位置关系是∗

A.相离 B.相交

C.相切 D.直线过圆心

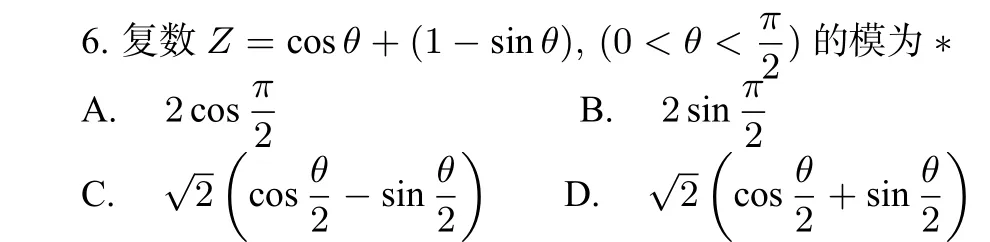
7.一个几何体的三视图(从左往右:正视图、侧视图、俯视图)如下,则该几何体的表面积是∗

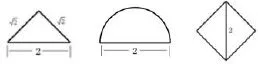
图1

8.运行以下程序时,执行循环体输出的数据是∗

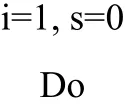
9.下列命题中是假命题的个数是∗

A.4 B.3 C.2 D.1

10.三棱锥P−ABC中,∠BAC=90°,M是BC中点,PM⊥面ABC,AB=AC=PM=2,则该三棱锥的外接球表面积是∗

A.2π B.4π C.9π D.10π

11.在一个边长为2的正方形OABC内,曲线y=ex−1和直线x=0,y=2围成阴影部分Ω.现向正方形AOBC内随机投一点(该点落在正方形AOBC内任何一点是等可能的),则所投的点落在阴影部分Ω的概率是∗

A.a＜b＜c B.a＜c＜b

C.b＜c＜a D.c＜b＜a

二、填空题(本大题共4小题,每小题5分,共20分,将正确答案填在答卷相应的位置上)

13.曲线y=ln(2x−1)在x=1处的切线与坐标轴围成三角形面积是____

16.整数列1,1,2,3,5,8,13,21,34,55,89,···,这便是奇妙的斐波那契数列,它有一些美妙的特性,比如:

(1)任何相邻两个数,它们的位置越靠后,第一个数与第二个数的比值越逼近黄金分割0.618,称为黄金比率;

(2)从第2项起,任何相邻的三个数a,b,c,前两个数之和等于第三个数,即a+b=c;

(3)从第2项起,每个奇数项b与它的前后两项a和c满足关系式:____.

三、解答题(6小题,共70分.解答应写出必要的文字说明,证明过程或演算步骤)

17.(本小题满分12分)为锻炼学生们的应用能力,数学老师把学生们带到学校操场,定位了学校操场上的东西方向上距离为40米的B、C两点,要求学生们利用工具做相关测量.一学生测得学校对面的小区楼顶A在B点的东偏北60°、仰角60°的方向上;楼顶A在点C的西偏北30°方向上.请你根据该生的测量结果:

图2

(1)计算小区楼高AO;

(2)求∠ACB的余弦值.

18.(本小题满分12分)某商场为吸引顾客消费推出一项活动:顾客消费每满100元可抽奖一次(例如:消费256元可不放回抽奖2次),并获得相应金额的返金券,已知抽奖箱中有形状大小相同的A、B、C三类奖券若干张.

(1)若抽奖箱中分别有A,B,C三类奖券5张、3张、2张,抽中A类奖券可以返券2元,B类奖券可以返券4元,C类奖券可以返券6元,某顾客消费328元,求返券金额不低于12元的概率.

(i)C类奖券有多少张?

(ii)从抽奖箱中任意摸出3张奖券,记得到C类奖券的个数为ξ,求随机变量ξ的数学期望Eξ.

19.(本小题满分12分)已知斜四棱柱ABCD−A1B1C1D1的棱长均为2,点M为线段CC1的中点,AB⊥AD,∠DCC1=∠BCM =60°,点 C1在面ABCD的投影Q∈CD

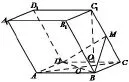
图3

(1)求证:平面ACM⊥平面BDD1B1

(2)求点O到平面ADM的距离

(3)求二面角B1−BM−D的大小

(1)求椭圆C的方程.

(2)四边形OANB是以ON为直径的圆的内接四边形.设抛物线E的焦点为F,直线AF与抛物线交于另一点M,求抛物线E的方程及△AOM的面积.

21.(本小题满分 12分)已知函数 f(x)=e|x−a|,g(x)=lnbx.

(1)当b＞0时,函数h(x)=xg(x)的最小值为−1,求b的值

请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.

23.(本小题满分10分)选修4-5:不等式选讲已知函数f(x)=|x−a|+|x−1|(a＞1)

(1)若对任意的x∈(−∞,1]时,f(x)+x2＞3恒成立,求实数a的取值范围;

(2)若不等式f(x)＞1的解集是{x|x＜1或x＞a},求实数a的值.

2017理科数学模拟试卷参考答案

一、选择题

ADADC CBABC DD

二、填空题

13.1 14.1009项 15.(0,2] 16.ac=b2−1

17解:依题意知 AO⊥底面BOC,BC = 40(米),∠ABO=60°,∠OBC=60°,∠OCB=30°.

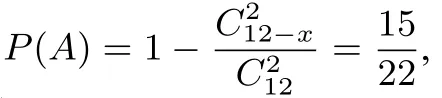
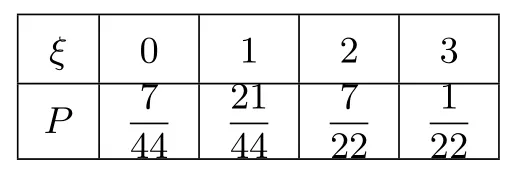
__ξ_ __0__ __1__ __2__ __3__ P 7 44 21 44 7 22 1 22-

(ii)随机变量ξ的取值为0,1,2,3,分布列是ABCD为正方形,∴AC⊥BD∵C1O⊆平面ACM,AC⊆平面ACM,C1O∩AC=O∴BD⊥平面ACM∵BD⊆平面BDD1B1,∴平面ACM⊥平面BDD1B1

19(1)证明:连结C1D,C1B,C1O由题意可知,△C1DC和△C1BC均为边长为2的等边三角形∴C1D=C1B,又O为线段BD的中点∴C1O⊥BD又四边形

图4

(3)二面角B1−BM−D的大小为90°

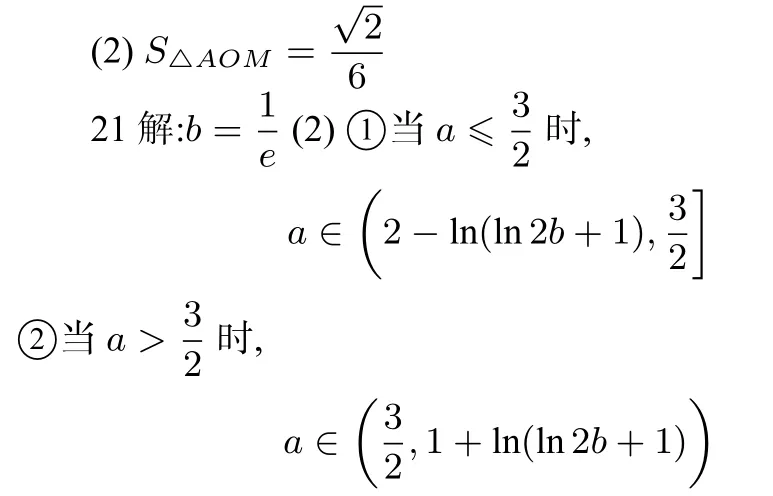
综上所述,a的取值范围为(2−ln(ln2b+1),1+ln(ln2b+1)).

23解:(1)实数a的取值范围是(3,+∞).(2)a=2.