分析法在数学教学中的运用*

广州市增城区增城中学(511300) 郑春立

分析法在数学教学中的运用*

广州市增城区增城中学(511300) 郑春立

分析法在解题过程中溯本求源,启发思维,梳理思路,突破难点,有着很好的引导作用;在分析题目的过程中,也能提高对知识的认识.在教学过程中,渗透分析教学,引导学生学会思考是很有必要的.以下是笔者在教学过程中的几点体会,以飨读者.

一、分析法在梳理思路,溯本求源的运用

立体几何考查学生空间几何想象能力,以及数量关系.对部分女生而言,“垂直”关系是“剪不断,理还乱”的问题.分析法,在立体几何的证明中,起着梳理思路,溯本求源的引导作用.

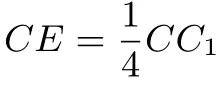
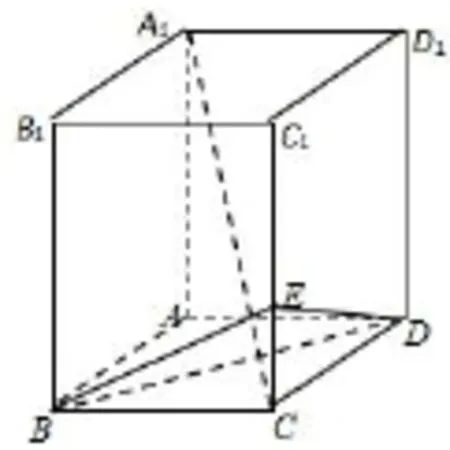
图1

(I)求三棱锥C−BED的体积;

(II)求证:A1C⊥平面BDE.

分析:(I)略

(II)有学生由平面AA1C⊥平面BDE推导A1C⊥平面BDE的错误.一方面学生对面面垂直推线面垂直的必要不充分条件的不理解;另一方面是对线面垂直与线线垂直转化的混乱.如果采用分析法,则思路就清晰许多:

其他解法略.由此可见在立体几何中,对于关系较为复杂的题目,用分析法追寻条件,整理思路,再用综合法条理书写是很有必要的.

二、分析法在化解抽象,突破难点的运用

必修三的算法案例,本意应该是体现算法运用,突出算法解决问题的思路.但是案例解题原理相对一部分学生而言,存在很大的理解障碍.如果在算法案例中,采用分析法分析算法.可以起到化解抽象,突破难点的运用.如辗转相除法求最大公约数的案例分析.如果按原理分析则比较严谨、但字母繁杂比较抽象.有些老师采用讲解的办法:如果除数与余数有公因数,那么这个被除数也有这个公因数,即除数与余数的公因数和被除数与除数的公因数相同.所以,辗转相除直至整除为止,即求最大公约数.这种分析,比原理分析简易许多,学生也较易接受.而笔者认为如果从实例出发,引导学生“倒叙”分析更易理解:由于辗转相除法最后一步被除数整除除数,即上一步除数与余数有公约数,由此,该公约数也是被除数与除数的公约数.而为何是“最大公约数”?能整除余数的最大约数也就是它本身.这样由具体例子分析原理题,引导学生回归具体过程,由具体到抽象,更易化解抽象问题,突破教学难点.

三、分析法在启迪思路、提高对知识认识的运用

应用题结合生活背景考查数学知识的应用,向来是学生比较薄弱且害怕的题型.分析法在如何提高学生的生活认识与知识的运用就有很好的引领作用.在《数列在日常经济生活中的应用》一课,笔者先帮学生预习了单利、复利以及分期付款规定等相关的经济知识,并加以例子解释.然后再以生活中常见的分期付款问题进行探讨.

例子:小华准备购买一台售价为5000元的电脑,采用分期付款的方式,并在一年内将款全部付清.商场提出的付款方式为:购买后2个月第1次付款,再过2个月第2次付款……购买后12个月第6次付款,每次付款金额相同,约定月利率为0.8%,每月利息按复利计算.求小华每期付的金额是多少?

在探讨过程中,引导学生往两种思路分析.

思路1:考虑小华每次还款后,还欠商场的金额.

思路2:小华在12月中共付款6次,它们在12个月后的本利和的累加与一年后付款总额相等.

学生按思路1很快通过列举找到等量关系,进而解决问题.但对于第二种思路,学生想不明,解释又很难讲透.我只好采用缓兵计暂时缓缓:方法2技巧性较强,但很难理解,如果不会可以用方法1,至于方法2,有兴趣的同学课后再与老师讨论.课后,学生甲询问第2种解法,但按授课时的思路分析还是讲不通.最后,我无奈地指第1种解法过程,引导她将解法1移项变形,问题能否将“购买一台售价为5000元的电脑”理解成“一次性存款5000元一年”,“分6次付款金额相同”是否相当于“6次分期等额存款”,“分期还清”是否等价于“一次性存款跟分期存款到年末的本利和相等”.令人惊喜的是:学生结合解法1的结果竟然很容易就理解了解法2.原来有时从答案出发,“倒叙”求解竟然是突破难点的一种捷径!

教学中的“教”是为了“不教”,在平时的教学中渗透分析教学,引导学生学会思考是很有必要的.

[1]普通高中课程标准实验教科书数学必修3[S].人民教育出版社.2013.

[2]郭秀玲.李忠海.学生数学问题表征能力分析[J],中学数学教与学,2009,(2)

*本文系广东省教育研究院2015年度课题“‘问题导学’模式下学生学习方式转变的教学策略研究”(课题编号:GDJY-2015-A-b057)的阶段性研究成果之一.