常考常新话“通径”
2017-03-28山东董敬红
山东 董敬红
(作者单位:山东省泰安英雄山中学)
常考常新话“通径”

圆锥曲线中涉及焦点的有关问题一直是高考数学考查的热点问题之一,因此也成了我们关注的“焦点”,其中有许多问题涉及圆锥曲线中最特殊的焦点弦——“通径”.
“通径”是圆锥曲线中最基本的一条线段,是过焦点的弦(焦点弦)中最特殊的一条.虽然现行教材中没有提及这一概念,而且在高考中是一个“小小”的考点,但也阻挡不了高考命题者对它的青睐,在历年高考中“出镜率”颇高,且常考常新.单就2016年高考来看,在九套试卷中,竟有三分之一(全国Ⅱ卷、Ⅲ卷和山东卷)对“通径”作了考查,由此可见一斑.“不以‘点小’而不为”,在我们的复习备考中应特别重视研究和发掘通径潜在的应用功能.
一、通径的定义
过圆锥曲线的焦点,作垂直于圆锥曲线对称轴的直线,则直线被圆锥曲线所截得的线段叫圆锥曲线的“通径”.
二、通径的性质

3.通径是圆锥曲线的最短的焦点弦.

【证明】如图,设直线l过椭圆的焦点F2交椭圆于A(xA,yA),B(xB,yB)两点.
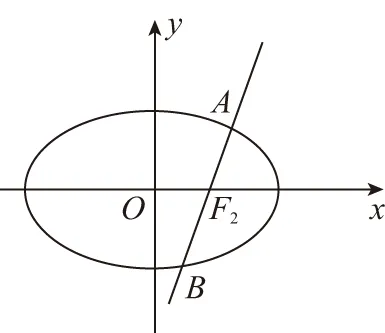

(2)当直线l的斜率k存在时,设直线l的方程为
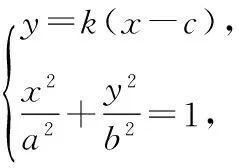
得(b2+a2k2)x2-2a2k2cx+a2(k2c2-b2)=0.
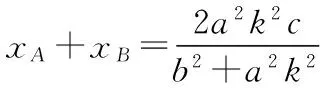
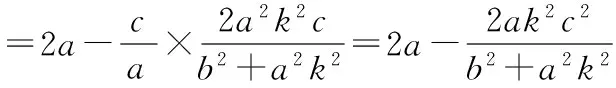

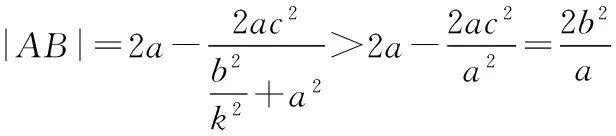

所以通径是椭圆最短的焦点弦.
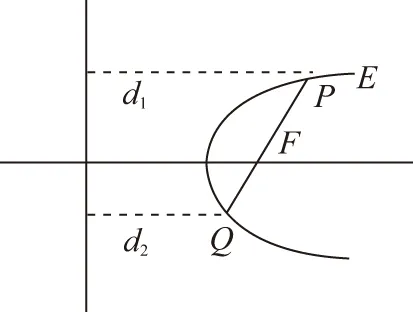
4.过圆锥曲线E的焦点F,作直线l交曲线E于P,Q两点,则半通径长的倒数是|PF|的倒数与|QF|的倒数的等差中项.
【证明】设圆锥曲线的焦点F到相应准线的距离为p,离心率为e,直线l的倾斜角为α,则过F的通径长为2ep,设P,Q到准线的距离分别为d1,d2,则d1=p+|PF|cosα,d2=p-|QF|cosα.
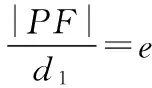
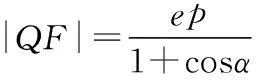
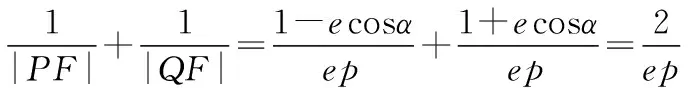
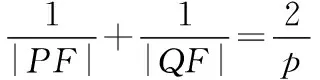
三、通径的应用
1.求曲线方程
【分析】过F1且垂直于x轴的直线被椭圆C截得的线段长即为通径长,于是建立关系利用待定系数法求解.
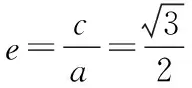

【点评】用待定系数法求圆锥曲线的标准方程时,从“定位”和“定量”两个方面去考虑.首先要“定位”,即确定焦点所在的坐标轴,这一点尤为重要;其次是“定量”,即利用条件确定方程中a,b的值,常通过待定系数法去求.本题中的通径长便是求解的关键.
2.求值
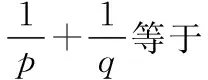
( )
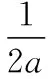
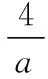
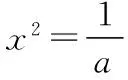
【解】选C.
【点评】本题虽然没有直接以通径的形式给出,但可以通过对条件的分析,转化为通径求解的.
【变式2】已知抛物线y2=2px(p>0)的准线经过点(-1,1),过抛物线的焦点F作x轴的垂线交抛物线于M,N两点. 若在x轴上存在点P,使得△PMN是等边三角形,则点P的坐标为________.
【变式3】已知抛物线y2=2px(p>0),直线l经过其焦点且与x轴垂直,并交抛物线于A,B两点,若|AB|=10,P为抛物线的准线上一点,则△ABP的面积为
( )
A.20 B.25
C.30 D.50
3.确定关系
( )
A.7倍 B.6倍
C.4倍 D.2倍
【分析】由线段PF1的中点在y轴上,坐标原点O是F1F2的中点,根据椭圆的对称性和三角形中位线定理可知PF2与x轴垂直,所以点P是通径的一个端点,|PF2|是通径长的一半.再结合椭圆定义便可确定出|PF1|与|PF2|的关系.

【点评】本题将“通径”暗含在题目的条件中,分析并挖掘出“通径”是解题的关键.
【变式4】过抛物线y2=2px(p>0)的焦点且垂直于x轴的弦为AB,O为抛物线顶点,则∠AOB
( )
A.小于90° B.等于90°
C.大于90° D.不能确定与90°的关系
4.求离心率

( )



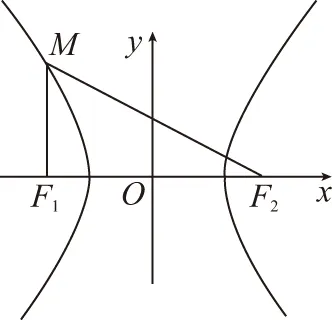
【点评】离心率是圆锥曲线的重要几何性质,是描述圆锥曲线形状的重要参数.圆锥曲线的离心率的求法和应用是一类常见题型,也是历年高考考查的热点.求解圆锥曲线的离心率的值或取值范围,其关键是建立恰当的等量或不等量关系,以过渡到含有离心率e的等式或不等式使问题获解.
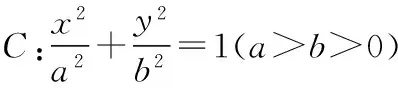
( )


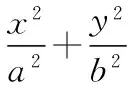
变式练习答案

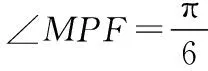
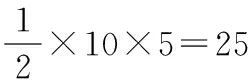
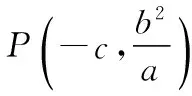
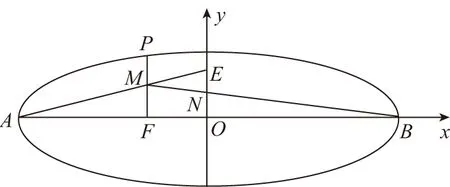
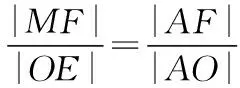
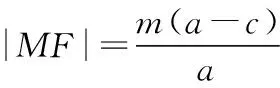
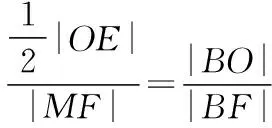
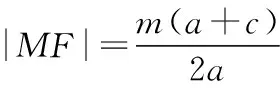

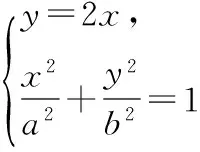
(作者单位:山东省泰安英雄山中学)
