透视新定义类导数题

安徽 李昭平 (特级教师)

(作者单位：安徽省太湖中学)

透视新定义类导数题

在高等数学与高中数学的知识交汇处命题是近几年高考命题的新趋势, 其中以导数为载体的新定义类函数题属高频考点. 此类问题往往具有背景新、结构新、覆盖面广、综合性强的特点，常常置于选择题、填空题或解答题靠后的位置，成为高考试卷的亮点.下面结合典型试题透视五大考点，供大家复习时参考.

1.定义函数的凸性

【例1】先阅读以下两个定义.

定义1：若函数f(x)在区间D上可导，即f′(x)存在，且导函数f′(x)在区间D上也可导，则称函数f(x)在区间D上存在二阶导数，记作f″(x)，即f″(x)=[f′(x)]′.

定义2：若函数f(x)在区间D上的二阶导数恒为正, 即f″(x)>0恒成立, 则称函数f(x)在区间D上为下凸函数.

已知函数f(x)=x3+ax2+b在x=1处取得极值.

【解析】(1)因为f(x)=x3+ax2+b, 所以f′(x)=3x2+2ax.

2.定义函数的驻点

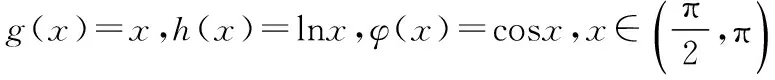
【解析】由g(x)=g′(x)，得x1=1.

【评析】本题定义函数的“驻点”,主要考查学生阅读、理解、迁移新知识的能力和数形结合的能力. 解题的基本步骤是：弄懂新定义，按定义求驻点，确定大小关系.

3.定义函数的拐点

( )

A.在直线y=-3x上

B.在直线y=3x上

C.在直线y=-4x上

D.在直线y=4x上

【解析】f′(x)=3+4cosx+sinx，f″(x)=-4sinx+cosx=0.由拐点的定义可知，f″(x0)=0，即4sinx0-cosx0=0，所以f(x0)=3x0+4sinx0-cosx0=3x0.

故M(x0，f(x0))在直线y=3x上. 选答案B.

【评析】本题以高等数学中函数的拐点与其二阶导数的关系为背景，通过给出二阶导数与函数拐点的定义(设置新情境)，考查学生阅读、理解、迁移新知识的能力.结合函数的凸性可知，其实“拐点”的几何意义是“函数图象上凸、下凸的分界点”. 解题的基本步骤是：弄懂新定义，按定义列式，发现函数关系.

元朔二年（前127年），卫青率数万骑兵从云中（今内蒙古托克托县）出塞，沿黄河西进，到达高阙（，阴山西北的缺口），切断了驻守黄河南原的楼烦王、白羊王与匈奴其他部落之间的联系。

4.定义函数曲线的新切线

【例4】若直线l与曲线C满足下列两个条件：(1)直线l在点P(x0,y0)处与曲线C相切；(2)曲线C在P附近位于直线l的两侧，则称直线l在点P处“切过”曲线C.

下列命题中正确的是________(写出所有正确命题的编号).

①直线l:y=0在点P(0,0)处“切过”曲线C：y=x3;

②直线l:x=-1在点P(-1,0)处“切过”曲线C：y=(x+1)2;

③直线l:y=x在点P(0,0)处“切过”曲线C：y=sinx;

④直线l:y=x在点P(0,0)处“切过”曲线C：y=tanx;

⑤直线l:y=x-1在点P(1,0) 处“切过”曲线C：y=lnx.

综上，正确答案是①③④.

【评析】本题以高等数学中曲线的切线与曲线的位置关系为背景，在课本函数曲线的切线定义的基础上再强化条件，得到直线l“切过”曲线C的新定义，主要考查导数的几何意义和相关应用，以及数形结合的思想.

5.定义与导数有关的新函数

【例5】M是由满足下列三个条件的函数f(x)构成的集合: ①方程f(x)-x=0有实根; ②函数f(x)的导函数f′(x)满足0

求证：方程f(x)-x=0至多一个实数根.

【解析】由条件①，可以假设方程f(x)-x=0有两个不相等的实数根α,β,则f(α)=α,f(β)=β,α<β.

由条件③知, 存在x0∈[α,β],使得等式f(β)-f(α)=(β-α)f′(x0)成立,即(β-α)(1-f′(x0))=0.

由条件②知，0

故方程f(x)-x=0至多有一个实数根.

(作者单位：安徽省太湖中学)