小题大做,别有洞天
——解决向量问题需要强化的五种意识
2017-03-28吉林林逸凡
吉林 林逸凡
(作者单位:吉林省长春市吉林大学附中实验学校)
小题大做,别有洞天
——解决向量问题需要强化的五种意识

向量问题灵活性强,活跃在各地的高考题、模拟题的选择、填空压轴题中,许多学生一直都是“想说爱你不容易”,本文以一道小题为例,总结解决向量问题需要强化的五种意识.


意识一:取基底

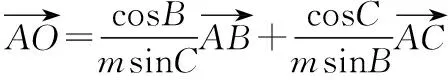


【点评】方法一的核心思想是“基底化”,优点是通用性强,缺点是计算量较大.选取两个不共线的向量为基底,则平面内所有向量都可以表示为这两个向量的线性组合.这个方法同样适用于解立体几何问题,只需选取两两不共线的三个向量为基底即可.

( )



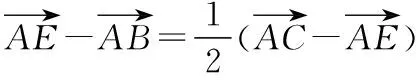


意识二:等式两边同时点乘一个向量,构造数量积



而∠AOB=2∠C,∠AOC=2∠B,OA=OB=OC=R,
将①②代入③可得



【解析】设∠AOC=α,


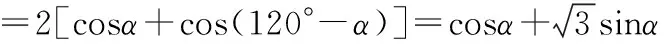
意识三:数形结合
【解法3】当cosB>0,cosC>0时,
如图,作平行四边形AEFD,

使AD=cosB,AE=cosC,

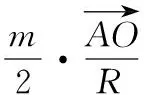





当cosB<0,cosC>0时,
如图,作平行四边形AEFD,
使AD=-cosB,AE=cosC,


当cosB>0,cosC<0时,同理可得.



意识四:先“拆”再“合”


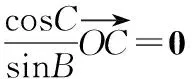



所以由②式可得-sin2B-sin2C+2msinBsinC=1,

【点评】方法四本质也是基底化的思想,与方法一有类似之处,只是不忙取基底,而是“先拆再整”:先“拆”,将向量拆成若干个特定向量的线性组合,再“合”,利用特定向量间的关系,化简式子.







( )
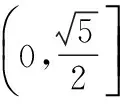





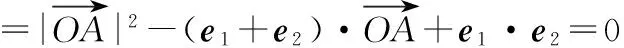

又由①②得


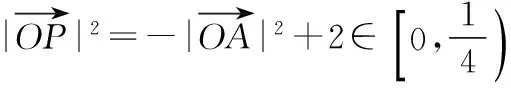

意识五:建系
【思路】建系设点,通过将向量坐标化解决.


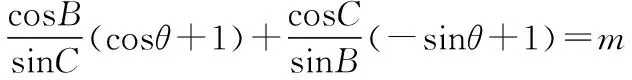


【点评】方法五的建系思想是常见且具有通用性的,在没有灵感的时候,只要建系建对,设点设好,理论上用建系的方法一定能解出来,在解决很多数量积的最值问题时,建系是一个不错的选择.
【变式5-1】同【变式4-2】.
【解析】如图,建立以A为坐标原点的直角坐标系,
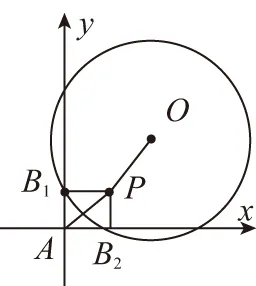

∴过点B1,B2作一个半径为1的单位圆,圆心为O(a,b).
设B1(0,y),B2(x,0),


得(x-a)2+b2=1,a2+(y-b)2=1,
两式相加得(x-a)2+(y-b)2+b2+a2=2,

∴|OP|2+|OA|2=2,

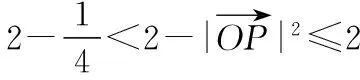

【变式5-2】同【变式1】.
【解析】由∠BAC=60°,AB=2,AC=1
可得∠ACB=90°,如图,建立直角坐标系,





(作者单位:吉林省长春市吉林大学附中实验学校)
