初中数学应用取向教学模式的探索
2017-03-24马俊勤
马俊勤

[摘 要] 全面的数学学习不仅有理论,更要有应用. 学以致用既是知识的巩固过程,也是理解的深化过程. 作为教学基础的初中阶段,更需要对学生的数学应用取向进行重点培养. 本文对当前的初中教学现状进行了广泛调研,并结合教育理论加以整合提炼,总结出了几个应用性教学的有效途径,望抛砖引玉,能启发初中师生.
[关键词] 初中数学;应用;教学模式;探索
对于初中数学教学的优化设计,应当一分为二地来看待,一是理论角度,二是应用角度. 所谓理论角度,就是从抽象理论出发,以基本概念、公式、定理等内容为基础,对数学内容进行数字化推导、分析. 而应用角度则是从具体实践出发,将理论知识投射到实际生活当中,在具体问题的解决中反映数学方法. 通过调研我们发现,当前的初中数学教学大多将主要精力集中在理论角度,而对应用角度的教学设计关注不够,这是教师们应当意识到并加以补足的.
与时事相结合,引领理论知识
应用
从实践的角度来讲,数学知识的学习是为了实际问题的解决. 如果能够让这个问题紧跟时代脚步,就可以更加彰显出初中数学的应用价值了. 选择与时事相结合的问题来引导应用,还可以将学生的思维热情激发出来,让大家对知识应用感兴趣,这对整体教学帮助很大.
例如,在一次课堂上,笔者先向学生讲述了这样一条新闻:根据环保相关部门的统计数据显示,20世纪初期,全球的鸟类动物与哺乳类动物的总和约为13000种,但在愈发严重的环境污染之下,截至20世纪末期,上述两种动物由于不断灭绝,其种类数量已经骤减了1.9%,其中,鸟类动物种类减少了1.5%,哺乳类动物种类减少了3.0%. (1)20世紀初期,这两种动物的种类数量分别是多少?(2)为了保护大自然,人们计划于21世纪末将鸟类动物和哺乳类动物种类的减少比例控制在0.9%之内,且将上述两种动物种类的减少数量比例控制在7 ∶ 6,为此,鸟类动物种类减少的数量上限是多少(计算结果精确到十位即可)?这个问题背景与时事联系非常紧密,话题一出,马上引起了学生的关注与讨论. 在这样的情感之下,大家自然很顺利地走进了数学问题的思考、分析当中. 学生们意识到,原来在前沿问题的解决中,数学知识也发挥着如此重要的作用.
时事本就比其他事物更容易吸引学生的关注. 将既有的知识方法运用到对这些问题的解答当中,能够瞬间唤醒学生的学习热情与自信,让大家乐于投入知识应用当中. 这对于推动学生的知识应用水平显然很有好处.
与图像相结合,引领理论知识
应用
初中数学的很多知识内容都与图像相联系,特别是函数内容,与图像的贴合就更加紧密了. 如果能够将这部分内容也以应用的形式反映出来,则不仅能加强学生对理论知识的理解,还可以训练大家数形结合的思维能力,可谓一举两得.
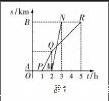
例如,为了深化学生对函数图像含义的理解,笔者特意设计了这样一道习题:A,B两地相距50千米,小张从A地出发,骑车前往B地. 小李驾驶摩托车也从A地前往B地. 两人运动中时间与路程的关系可以表示为图1当中的图像,其中折线PQR表示小张的运动过程,线段MN表示小李的运动过程. (1)小张和小李的出发时间相隔多久?(2)当小李追上小张时,小李出发了多长时间?此时,他们距离B地还有多远?这道题的实质是训练学生从图像中分析函数关系的能力. 如果只是刻板地给出图像、提出问题,难免会让学生感到枯燥乏味. 当其建立在应用的背景上时,效果就完全不同了. 这种实际的运动状态,对于学生的理论分析也很有帮助. 在这种方式的启发下,教师可以考虑将更多形式的函数知识照此呈现,生动地优化学生的理解效果.
图像元素的融入,为知识应用注入了新的活力. 在这种创新性的题目形式之下,学生的思考热情明显提升了许多. 这样的形式,不仅深化了学生对函数理论本身的理解,还巧妙地将函数图像的知识整合了进来,让学生在一次练习中得到了多角度的提高.
与空间相结合,引领理论知识
应用
在初中阶段的知识学习中,既有代数内容,也有几何内容. 这种知识结构的特点在知识应用环节自然也应当有所体现. 笔者在教学过程中多次运用了几何内容的应用性提问,均收获了较为理想的训练效果.
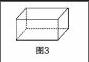
例如,笔者曾经以几何内容为背景,为学生设计了这样一个问题:某礼品商店准备自主制作A,B两种规格的无盖长方体纸盒(图2为A规格,图3为B规格). 为了节约成本,商店打算用之前剪裁剩下的纸板进行制作,将之分别修剪成长方形与正方形两种形状(如图4所示),且正方形的边长等于长方形的宽. 若商店共裁剪出300张长方形纸板和150张正方形纸板,且无须考虑连接处的损耗,那么,可以分别制作出两种纸盒各多少个?虽然这个问题的解答方法是方程,但首先需要学生做的是对题目条件当中所给出的几何图形进行空间性的理解,明确了题意才能准确解题. 为了方便理解,学生纷纷拿出废纸进行操作演示,于模拟已知条件的过程当中实现了空间想象能力的提升,训练效果很好.
从几何内容出发设计应用问题,并不一定是将问题内容仅仅局限于几何范围之内. 如果能够将几何与代数的元素加以融合,效果自然更佳. 通过结合几何知识内容开展知识应用,学生不仅能关注到解答问题所要用到的理论方法,还能在分析题目条件时训练自己的空间想象能力,这对于日后的长远数学学习很有好处.
与统计相结合,引领理论知识
应用
除了上述几个途径之外,将数学知识与统计形式相结合,也可以很顺利地引导学生建立数学应用取向. 其实,在实际生活当中,待解决的问题以统计图表的形式呈现出来,也是很常见的形式. 因此,将之在课堂训练中予以体现也十分必要.
例如,带领学生学习了方程的知识内容后,笔者请大家试着解答了这样一个应用问题:某农场准备种植水稻、棉花和菠菜三种作物,该农场中可以用于作物种植的土地面积是51公顷,共有工人300人. 经过调研与估算,管理人员将三种作物种植的劳动力需求及相应的资金投入需求整理汇总成了表格(表1). 目前,农场预备投入67万元的资金用于上述三种作物的种植,那么,为了让这些资金恰好够用,又可以让每一名工人都有工作,应当怎样分配这三种作物的耕种面积?这道题的特别之处在于,关键性的已知条件并没有按照惯常的方式以文字叙述来表示,而是将之体现为统计表格的形式. 这就在无形中为学生添加了统计数据分析的任务. 然而,在实际应用的问题情境之下,学生并没有感到厌烦,而是在学以致用的乐趣当中同步完成了统计数据分析与方程思维训练的任务,教学效果十分理想.
在统计的形式下应用数学知识,可以说是学以致用的一种升华,它不仅巧妙触发了学生的知识能力,还训练了学生识读统计数据的能力. 一方面,这是数学学习必不可少的能力,另一方面,它也让知识应用的过程更加真实.
应用能力对于初中数学教学的价值不言而喻. 没有应用的数学理论是缺乏生命力的,于数学能力的角度来讲,更是不完整的. 只有从理论与应用两个角度双管齐下,才能设计出全面高效的数学教学,实现学生知识能力的系统式提升. 知识应用是一个较广的范畴,依据不同特点将之进行划分,可以让数学教学更有条理,逻辑清晰. 引导学生在初中数学学习中建立起应用取向,是每个教师需要重视的.
