浅谈初中数学教师解题能力的培养

葛铁雷

[摘 要] 数学教学中，如何教会学生解题是每一个数学教师需要正视的课题. 要教会学生解题，数学教师本身就要会解题，懂解题. 本文根据笔者多次参加数学青年教师基本功大赛的经验和平时的解题教学，提出了关于初中数学教师解题能力培养的一些建议，给大家提供参考.

[关键词] 教学教师；初中数学；解题能力

江苏省初中数学青年教师基本功比赛从2010年开始举办，至今已进行了3届. 从一开始的摸索，到现在赛事的日趋规范，笔者有幸参加了其中多次比赛，获得三次南通市一等奖，一次江苏省一等奖. 江苏省赛制分为通用技能和专业技能两大项，通用技能分粉笔字、即兴演讲、教学设计与课件制作、模拟上课，占总成绩的60%；专业技能分基础知识测试和解题能力测试、闭卷笔试，占总成绩的40%. 解题能力在基本功比赛中占着非常重要的地位，解题能力也是数学老师专业素养的一个重要体现，一个数学老师解题能力糟糕可不是一件好事情. 如何锤炼自己的解题能力？下文是笔者的一点小体会.

“数学难，学习数学更难”，很多人对数学望而生畏，每年的中高考数学考试的难易程度都会成为当季的热点话题. 很多孩子怕做数学题，有的同学怎么想都想不到解题方法，而有的人却能轻松地给出非常精妙的答案. 美国著名数学家在《怎样解题》中有这样一句话：“一个重大的发现可以解决一个重大的难题，而在解答任何一道题目的过程中，也会有点滴的发现. ”这句话有非常重要的现实意义，教师怎样提高自身的解题能力并帮助学生学会解题，是我们每一位数学老师应该认真思考的重大问题.

教师应当“下题海”

数学老师不做题还能成为数学老师吗？每一位初中数学老师应当潜心研究各地的中考试题. 每年中考结束后，网上会出现大量的中考真题，适逢暑假期间，老师在享受假期之余，不能忘记收集这些新鲜出炉的试题，并一道道做过去. 这不仅能训练自己的解题能力，更能够把握住本地中考数学试题的思路与灵魂，以此为导向来指导平时的教学. 这不单是初三老师的事情，同样是初一、初二老师的任务. 每个地方中考题的命题趋势不是一蹴而就的，而是日积月累逐渐形成的，需要我们从初一到初三时时关注. 我们同样需要关注其他地市的中考试题，了解当下的命题理念和命题的热点.

不单是中考试题，我们还需要将教科书和教辅资料认真做一遍，了解教科书编排的目的，更好地服务教学. 教师深入“题海”，才能让学生不入“题海”.

教师解题时应“一题多法”

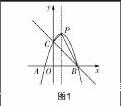
数学老师解题时最忌讳“就题论题”，一道题目解过之后不再细致地分析，解题方法单一会产生思维的局限，这样教出的学生也会受教师思维局限性的影响. 例如，以二次函数为基本背景的三角形面积问题是近年来考试的热点题型：如图1，已知抛物线y=-x2+2x+3与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C，抛物线的对称轴与抛物线交于点P，连接PC，PB，求△PCB的面积.

这一问题虽然简单，但我们在解决这一题时，应“一题多法”，提出不同解决问题的方法，然后总结出解决这一类问题的一般方法.

这样一道题有诸多解法，教师应及时整理，总结出此类问题的一般解法. 所以教师在解题时，不能拘泥于一种解法，要常转换思路，使用多种想法，才能更好地提高自己的解题能力.

教师解题时应注意“多题一法”

不会整理试题的数学老师不是一个合格的数学老师. 每一位数学老师都应当具有自己的习题库，习题库里不能只是网上直接下载的试题分类，应当自己细化到每一个知识点，每一种方法. 当前教育背景下，数学老师的最终任务，其实就是解题经验的教学. 所以教师在解题时，应及时分门别类，把用同种方法解决的问题总结起来，特别注意“多题一法”，以电子文档的形式加以整理，这样才能做到有的放矢，游刃有余.

例如，学习“相似”这章时，有一类题目常常借助直角来构造相似（或全等）模型来解决问题.

如下面几道题：

1. 如图7，AB=4，射线BM和AB互相垂直，点D是AB上的一个动点，点E在射线BM上，2BE=DB，作EF⊥DE并截取EF=DE，连接AF并延长交射线BM于点C. 设BE=x，BC=y，则y关于x的函数解析式是（ ）

2. 一块直角三角板ABC如图8放置，顶点A的坐标为（0，1），直角顶点C的坐标为（-3，0），∠B=30°，则点B的坐标为______.

教师解题时应注意“一题多变”

教师每做完一道题，都应当静下心来，去挖掘此题的内涵与外延，尝试着去改编.

1. 改变题目的题设

此题先把分式方程转化为整式方程，然后用含a的代数式表示这个解. 由于方程有增根，增根是化为整式方程后产生的不适合分式方程的根，因此应先确定增根的可能值. 由最简公分母x-1=0，得到x=1，然后代入整式方程算出未知字母的值. 教師在做这一题目时，应及时将题目改编如下：

通过这样的改编，能让学生充分熟悉分式方程中解的相关题型，从一道题引申出一类题，以一管窥全豹.

2. 改变题目的背景

例2 如图10，正方形ABCD内有一点P，且PA=1，PB=2，PC=3，求∠APB的度数.

此题为旋转中的一道经典题，如图11所示，将△APB绕点B顺时针旋转90°，构造出了等腰直角三角形BPP′和直角三角形PP′C，进而解决问题. 教师在解决这一题时，可以改变题目的背景，将问题放在等边三角形中研究，改编如下：如图12所示，等边三角形内有一点O，已知OA=4，OB=3，OC=5，求∠AOB的度数.

教师及时总结：在遇到正三角形内的点、正方形内的点等问题时，常将某图形旋转60°，90°等. 因为正三角形的三条边相等，内角等于60°，旋转后的图形的一边依然是等边三角形的边. 如图13中△BOA旋转后，BA正好与BC重合.

3. 交换题目的题设与结论

在初学相交线与平行线时，有这样一道题：如图14，一名同学经过测量，∠BAE=∠AEC=∠ECD=120°，他就断定AB∥CD，你认为合理吗？请说明理由.

解决此例时可过点E画AB的平行线，进一步证明EF∥CD，从而利用平行公理的推论证明出AB∥CD.

做完此例，可以交换题目的题设和结论，改编如下：

如图15所示，已知AB∥CD，猜想∠A，∠E，∠C三个角的数量关系，并证明你的猜想.

通过这样的改编，学生能进一步巩固平行的判定和性质，熟悉平行公理的推论.

经过这样长期的实践和积累，每一位教师解题能力必将得到长足的进步，业务水平将得到极大的提高，思维水平也必将是活跃的. 在教学过程中，教师也可以将自己的解题理念传输给学生，这样思维训练下的学生，思路肯定能得到很好的拓展，也能培养学生探究与钻研的精神，学生的解题速度、解题技巧、解题的规范性也会得到很大的提高. 与此同时，经过这样的锻炼，教师也能积累出专属于自己的题库，不时地加以更新，在遇到不同教学内容时，都有自己精心整理的题目辅助教学，为自己的备课带来事半功倍的效果.