基于混合范数的来波方位估计
2017-03-23谢前朋王伦文
谢前朋,王伦文
(解放军电子工程学院,安徽 合肥 230037)
基于混合范数的来波方位估计
谢前朋,王伦文
(解放军电子工程学院,安徽 合肥 230037)
针对传统MUSIC算法以及CS-MUSIC算法在相干和非相干信源的条件下DOA估计效果不理想问题,提出基于混合范数的来波方位估计方法。该方法利用MUSIC和压缩感知稀疏恢复的特性得到信号的支持域,然后由信号的支持域得到噪声子空间和信号子空间,把得到的信号子空间和噪声子空间与经典MUSIC算法相结合,得到高分辨率的来波方位估计方法。仿真结果表明,在非相干信源的条件下,该算法性能优于MUSIC和CS-MUSIC算法;同时,该算法相关信源的角度分辨率也优于CS-MUSIC算法。
DOA估计;CS-MUSIC;压缩感知;混合范数
0 引言
窄带远场信号的来波方位估计在无线通信、雷达声呐系统、声源定位、医学成像和地震学中得到了广泛的应用。经典子空间估计算法如MUSIC算法在理想的条件下能得到高分辨率的来波方位估计,但是,在信噪比比较低和快拍数比较小的情况下,其会产生子空间泄露问题[1],即一些信号子空间泄露到噪声子空间之中从而导致算法性能的下降。同时,MUSIC算法同样也不能处理相关信源的DOA估计问题。
由于信号在空间域的稀疏性,空间信源数远远小于所有可能划分的空间角度数,使压缩感知在DOA估计中得到了广泛的应用。压缩感知能降低采样速率以及传感器阵列的数目,同时在工程上能降低软件与硬件的复杂度。
压缩感知中的稀疏恢复算法能在未知的稀疏矢量空间中找到非零元素的位置,这在DOA估计中非常重要,常用的稀疏恢复算法是凸优化算法[2-3]和贪婪算法[4-5]。贪婪算法能够降低计算的复杂度,凸优化算法一般是基于l0,l1,l2范数。在这三种范数中,l2范数存在非稀疏解[6],使用l0范数能够得到精确的解但是会导致NP-hard问题[7]。因此,在特定的条件下,l1范数被用来对稀疏信号进行精确恢复,使其和l0范数有相同的解[8]。三种算法均能够处理单快拍和多快拍数条件下的DOA估计,分为单观测矩阵矢量算法和多观测矢量矩阵算法。但是,三种算法在单独使用时都会出现不足。本文针对上述问题,提出了基于混合范数的来波方位估计方法。
1 信号模型
1.1 基于MUSIC算法的信号模型
假设N个窄带远场信号源si(t)入射到M元均匀线阵上,接收信号模型可以表示为如下:
X=AS+W
(1)
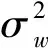
以MUSIC算法为代表的传统DOA估计算法基于奇异值分解,利用噪声子空间和信号子空间的正交性来实现高分辨率的DOA估计。接收信号的协方差矩阵为:
RXX=E{XXT}
(2)
对RXX进行奇异值分解,得到信号子空间QS∈CM×N和噪声子空间QW∈CM×(M-N),从而得到MUSIC算法的空间谱估计如下:
(3)
由于信号子空间与噪声子空间的正交性,利用MUSIC算法进行测向时,得到的最大的峰值方向就是信号的来波方向。在高信噪比的条件下,MUSIC算法能得到较好的性能,但是其有两方面的不足[9]:需要知道信源的个数以及只能对非相干信源进行DOA估计。
1.2CS-MUSIC
把空间角度划分为G份,[θ1,θ2,…,θG],G≫N,在稀疏域的DOA估计模型如下:
X=ΨS+W
(4)
式(4)中,S=[s1(t),…,sG(t)]T中有N个非零的列,Ψ∈CM×G是过完备原子基。利用l1范数对上式进行求解,找出S中最大的N个元素值:
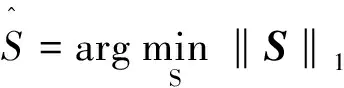
(5)
在快拍数为单快拍的条件下,对应的模型是单测量矢量模型(Single Measurement Vectors,SMV),否则是多测量矢量模型(Multiple Measurement Vectors, MMV)问题。对于单快拍SMV问题,除了凸优化的解决方法,贪婪算法通过迭代运算也能得到稀疏系数的解。对于SMV问题的求解最常用的两种贪婪算法是正交匹配追踪和基追踪算法。对于MMV问题,算法应该能恢复出联合稀疏矩阵S。一般使用混合范数来求解联合稀疏矩阵S:
(6)
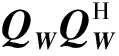
(7)
式(7)中,j⊂{1,…,G}表示Ψ的列。在相干信源的情况下,rank(S)=r (8) 图1的流程图说明了本文所提算法的步骤,压缩感知是以概率性的方式重构空间谱,而MUSIC算法是以确定性的方式构造空间谱。压缩感知突出的优势是在较少的快拍数的情况下具有较高的分辨率,其特殊的重构方式使得该方法具有抗干扰性,但随着快拍数的增加,压缩感知算法不能给出尖锐的谱峰,而MUSIC算法在快拍数较多时能得到尖锐的谱峰。因此使用混合l1,2范数与MUSIC算法相结合能实现比其他MMV稀疏恢复算法或传统DOA估计算法更好地测向性能。 利用本文算法来进行来波方位估计包含以下三个步骤:1)由于本文算法在处理DOA估计时,需要知道信号源的数目,因此,在信源数目未知时首先利用盖氏圆方法(Gerschgorin)[11]对信号源数目进行估计,盖氏圆方法在相关信源,白噪声和色噪声的条件下均能精确的估计出信源数; 2)在得到信号源数目的条件下,利用l1,2范数最小化求出SuppS(N-r);3)找出SuppS中剩余的r个元素,然后使用MUSIC算法进行DOA估计。为了降低式(4)中X的维数,首先进行奇异值分解: X=UDrVT (9) 式(9)中,Dr∈Cr×r是包含最大奇异值的满秩对角矩阵,U∈CM×r和V∈CK×r分别是对应的酉矩阵。降维后的信号模型为: XSV=ΨSSV (10) 式(10)中,XSV=XV,SSV=SV。把降维后的式(10)首先利用l1,2范数最小化求出SuppS(N-r)的下标: (11) 式(11)中,σ2表示稀疏恢复需要的噪声门限,把通过上式求出的SuppS记为IN-r。然后通过MUSIC算法找出SuppS中剩余的r个下标。从Ψ中选择下标为IN-r的元素记为ΨIN-r从而形成新的噪声子空间。对于其他下标的元素利用式(8)找到非零元素的下标并且按升序排列。 本文提出一种新的混合l1,2-MUSIC算法,尽管l2,1-MUSIC算法在文献[12]中被提出,但是本文算法从另一个角度来对来波方位进行估计。所提算法把压缩感知以概率性的方式重构空间谱和MUSIC算法以确定性的方式构造空间谱结合起来。并且使用新的两种范数对信号进行恢复同时不需要考虑信源的相关就能得到完整的信号支持域SuppS,克服了传统MUSIC算法以及CS-MUSIC算法的不足。通过在划分的空间网格上重新排列SuppS的下标,利用压缩感知稀疏恢复算法能得到精确的高分辨率信号的来波方位。 由于在实际的来波方位估计中,正弦信号、高斯信号和线性调频信号得到了广泛的应用,本文把这三种信号应用于所提出的算法中,通过本文算法在三种不同信号中的应用来说明所提算法能够应用于实际的信号来波方位估计中。 为了说明本文算法的有效性,通过与MUSIC算法以及CS-MUSIC算法进行对比。算法的性能通过不同信噪比下的均方误差、不同快拍数下的均方误差以及对相关信源的分辨能力来进行说明。分别在信源为正弦信号、高斯信号以及线性调频信号的情况下比较三种算法的性能。同时定义克拉美罗界如下[13]: (12) 式(12)中,K表示快拍数,M表示阵元的数目,d表示阵元间距,θ表示方位角。 3.1 不同信噪比下的均方误差实验 正弦信号的频率设置为100 Hz,高斯信号的方差设置为σ=0.01,线性调频信号的频率随时间线性变化,初始值设置为100 Hz,以0.1 Hz的速率进行增加。所有的结果是100次独立蒙特卡罗实验的平均,图3表示三种算法的均方误差随信噪比的变化。阵元数为10,阵元间距为λ/2,采用50个快拍的接收数据。信噪比的变化范围为[-5,20]dB。入射信号来自于40°方向,把[0,180°]的角度划分间隔为1 801份。对于MMV问题下的SuppS,本文算法通过混合l1,2范数最小化和MUSIC算法来求解,而CS-MUSIC通过SOMP和MUSIC来求解。 从图2中可以看出:当信号为正弦信号时本文算法的性能优于MUSIC算法以及CS-MUSIC算法;但对于高斯信号以及线性调频信号在信噪比较低时,本文算法性能差于其他两种算法。这是因为高斯信号以及线性调频信号在频率域不具有稀疏性。 3.2 不同快拍数下的均方误差实验 快拍数的变化范围为[1,1 000],阵元数为12,SNR=0 dB,信源来波方位为40°,其他实验条件不变。从图3中可以看出在低快拍数的条件下,本文所提算法优于MUSIC算法和CS-MUSIC算法。 3.3 三种算法对相关信源的分辨率实验 两个相关正弦信号来自于不同的方向,阵元数采用20,快拍数为200,信噪比SNR=0 dB。第一个信源的角度为-1°,第二个信源的角度在第一个的基础之上以0.1°的速率进行增加。真实的信源间隔应该是一条直线。由于MUSIC算法不能处理相关信源,所以只对本文算法和CS-MUSIC算法的性能进行比较。从图4中可以看出:本文算法能够分辨的角度间隔是0.5°,而CS-MUSIC算法能够分辨的最小的角度间隔为0.7°;并且在角度间隔小于0.5°的条件下,本文算法的性能优越于CS-MUSIC。 通过以上仿真实验可以得出,本文提出的新的混合范数的方法的确提高了来波方位的估计性能。并且针对不同的信号进行了分析,因此,本文所提算法在实际的情况下也能对信号进行来波方位估计。 本文提出基于混合范数的来波方位估计方法。该方法利用压缩感知稀疏恢复的混合l1,2范数对噪声子空间和信号子空间进行稀疏恢复,得到一种新的高分辨率的来波方位估计方法。仿真结果表明,在非相干信源和相干信源的条件下,本文算法性能优于MUSIC和CS-MUSIC算法。但是,本文算法的测向性能仍然不能达到克拉美罗界,同时当角度间隔小于0.5°时,本文算法不能精确地分辨出两个信号;并且,本文算法需要预估计信源数,而且阵元数要多于信源数。对于信源数未知的情况下,在下一步的研究中可以在DOA估计之前,先利用最新的信源数目估计算法对来波数目进行精确地估计,然后再利用本文所提的算法对信号的来波方位进行精确恢复。 [1]Shaghaghi M, Vorobyov S A. Subspace leakage analysis and improved DOA estimation with small sample size[J]. IEEE Transactions on Signal Processing, 2015,63(12):3251-3265. [2]蔡晶晶,宗汝,蔡辉.基于空域平滑稀疏重构的DOA估计算法[J].电子与信息学报,2016,38(1):168-173. [3]时洁,杨德森,时胜国,等.基于压缩感知的矢量阵聚焦定位方法[J].物理学报,2016,65(2):1-11. [4]黄麟舒,察豪,叶慧娟,等.均匀线阵目标到达角估计的压缩感知方法研究[J].通信学报,2015,36(2):1-7. [5]沈志博,董春曦,黄龙,等.一种基于稀疏分解的窄带信号频率估计算法[J].电子与信息学报,2015,37(4):907-912. [6]李喆,桑海风,徐维华.欠定非线性系统极小二范数解的可信误差界[J].吉林大学学报(理学版),2015,53(3):414-418. [7]伍飞云,周跃海,童峰.基于近似零范数和混合优化的压缩感知信号快速重构算法[J].自动化学报,2014,40(10):2145-2150. [8]Qaisar S, Bilal R M, Naureen M, et al. Compressive sensing : from theory to application[J]. Journal of Communications and Networks,2013,15(5):443-456. [9]闫锋刚,沈毅,刘帅,等.高效超分辨波达方向估计算法综述[J].系统工程与电子技术,2015,37(7):1465-1475. [10]Majumdar A, Ward R K, Aboulnasr T. Algorithms to approximately solve NP Hard row-sparse MMV Recovery problem: Application to compressive colcor imaging[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2012,2(3):362-369. [11]赵拥军,李东海,赵闯,等.宽带阵列信号波达方向估计理论与方法[M].北京:国防工业出版社,2013:99-107. [12]Wu X, Deng W, Yang Q. DOA estimation based on MN-MUSIC algorithm[J]. Journal of Information and Computational Science, 2014,11(8):2611-2620. [13]罗鹏飞,张文明,刘忠,等.统计信号处理基础-估计与检测理论[M].北京:电子工业出版社,2011:23-29. DOA Estimation Based on Mixed-Norm Algorithm XIE Qianpeng, WANG Lunwen (Electronic Engineering Institute of PLA, Hefei 230037, China) In order to solve the poor performance of the traditional MUSIC algorithm and CS-MUSIC algorithm DOA estimation in the condition of coherent and incoherent sources, an approach based on Mixed-Norm of compressive sensing was proposed in this paper. The proposed method used the characteristics of MUSIC and compressive sensing sparse recovery to obtain the support of the signal domain, then the noise subspace and signal subspace were obtained by the support of the signal domain. Finally, an approach was obtained based on the combination the signal subspace and noise subspace with classical MUSIC algorithm. Simulation experimental results proved that the proposed method had superior performance than MUSIC and CS-MUSIC algorithm under the condition of incoherent source. At the same time, the algorithm‘s angular resolution was also superior to CS-MUSIC algorithm under the condition of coherent source. DOA estimation, CS-MUSIC, compressive sensing, mixed-norm 2016-9-23 国家自然科学基金项目资助(61273302) 谢前朋(1991—),男,河南郸城人,硕士研究生,研究方向:智能信号处理。E-mail:13721038905@163.com。 TN911.7 A 1008-1194(2017)01-0071-052 基于混合范数的来波方位估计方法
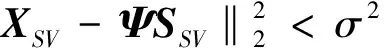
3 实验验证
4 结论
