B-S期权定价模型在财险定价中的应用

李子耀，黄洪瑾

（安徽财经大学，安徽蚌埠233030）

一、期权定价应用于财险定价中的可行性分析

（一）期权与财产保险具有相似性

财产保险和期权实质上都是一种避险工具，它们在很多方面都具有相似性。投保人向保险公司支付一笔保险费，获得当标的物发生损失时，向保险公司请求赔偿的权利，在保险期间内，如果标的物没有发生损失，则保险公司就不必承担损失赔偿责任，投保人损失保费，这就相当于期权的买方在期初购入一份期权合约，在到期日期权标的物的价值与约定的执行价格相同，这样期权的买方就无法从卖方处获得经济利益，还会损失一笔期权费。如果在保险期间内，投保人投保的标的物发生损毁，保险公司就有义务按照合同的约定对投保人进行补偿，这在期权中就相当于在到期日时标的资产发生减值，期权的买方有权按照合约将减值的标的资产以约定的价格卖给期权的卖方，这样就规避了标的物减值的风险。简单地说，投保人缴纳保险费购买保险合同，就相当于购买了一份美式看跌期权，在标的物发生减值时，可以按约定的价格将受损标的物“卖给”保险公司，达到转移风险的目的。

下面通过图像进一步说明保险与期权之间的相似性：

在看跌期权中，假设期权费为P，执行价格为X，标的资产的价格为S。则当S〈X-P时，买方盈利，且盈利随S的减小而增大，但最大不超过X-P；当S=X-P时，买方损益为0；当X-P〈S〈X时，买方亏损，且亏随随着S的增大而减小，但最大亏损不超过X；当S≥X时，买方亏损恒定，等于期权费X。这样就可以做出如图1所示的看跌期权价值示意图。

在财产保险中，也可以做出类似的图像（如图2），图1中看跌期权的期权费P就相当于图2中的保险费，执行价格X就相当于保险金额。虽然二者也存在着许多差异，但是期权费和保险费的定价思想是一致的［1］。

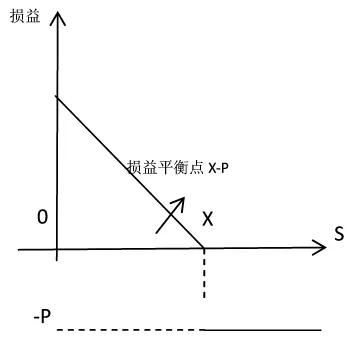
图1

图2

（二）相同的定价基础

B-S期权定价模型的基础是随机游走理论，该理论的核心思想是证券价格的时间序列呈现随机状态，随机游走模型分为两种，其数学表达式分别为：

其中，①式称为“零漂移的随机游走模型”，即资产或证券的价格是在前一天的基础上进行随机变动的，价差全部包含在随机项中。②式称为“α漂移的随机游走模型”，这一模型中，资产或证券的价差包括两部分，一部分包含在固定变动α中，另一部分也包含在随机项中。

通过上面的分析我们可以看出，期权和财产保险在定价思想和定价基础上都很相似，所以将B-S期权定价模型应用在财产保险定价中是可行的。

二、B-S期权定价模型简述

B-S期权定价模型是由罗伯特·默顿 （RoBert Merton）和迈伦·斯克尔斯（Myron Scholes）于20世纪70年代提出的，这一定价模型的提出不仅解决了期权定价的问题，而且为金融市场上的其它衍生金融工具的定价提供了新的思路。此外，直到今天，该模型以及它的一些变形也被投资银行、金融管理者、保险人等广泛应用。

B-S期权定价模型有以下几个重要假设：（1）标的资产价格行为服从对数正态分布模式；（2）市场无摩擦，即不存在税收和交易成本，标的资产可以自由买卖；（3）金融资产在有效期内无红利及其他所得；（4）该期权在到期前不可实施，即该期权是欧式期权；（5）不存在无风险套利的机会；（6）证券市场是连续的；（7）无风险利率r为一已知常数。

基于上述假设，他们推导出了计算欧式看涨期权和欧式看跌期权价值的公式：

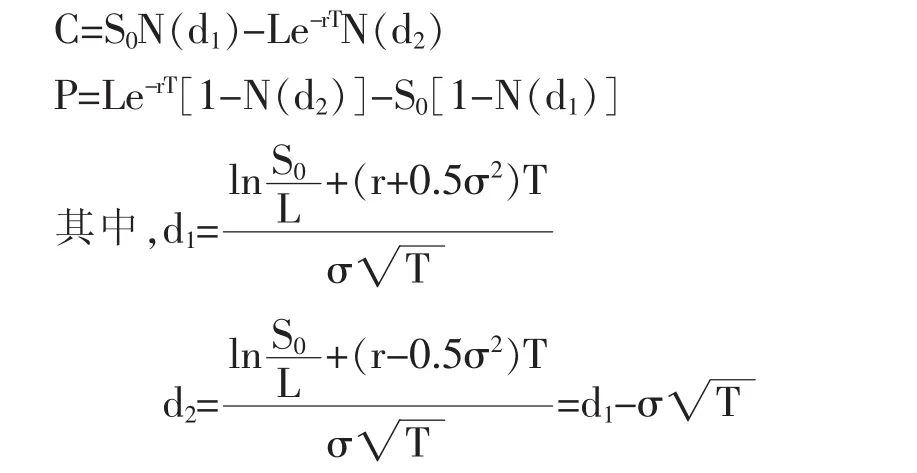
式中，C为欧式看涨期权的合理价格；P为欧式看跌期权的合理价格；N（d1）、N（d2）分别为 d1、d2的累计概率分布函数；S0为所交易金融资产的当前价格；L为期权的执行价格；T为以年为单位的期权的有效期；r为连续复利计无风险利率；σ2为年度化方差。

三、B-S期权定价模型在财险定价中的实证分析

下面以某保险公司的家庭财产综合险为例，说明B-S期权定价模型在财产保险定价中的应用。

这里选用5万、10万、15万、20万为可能的标的资产价格，绝对免赔率选用5‰、10‰、20‰、30‰，到期时间为一年，无风险利率采用2016年第11期1年期固定利率债券的票面利率2.55%，资产波动率分别为3%、5%、7%。

整理得：=5，10，15，20

L=4.975，9.95，14.925，19.9（当绝对免赔率为 5‰时）

σ=3%，5%，7%

r=2.55%

当标的资产价格为10万元，绝对免赔率为5‰，资产波动率为3%时，

先计算出 d1、d2的值：

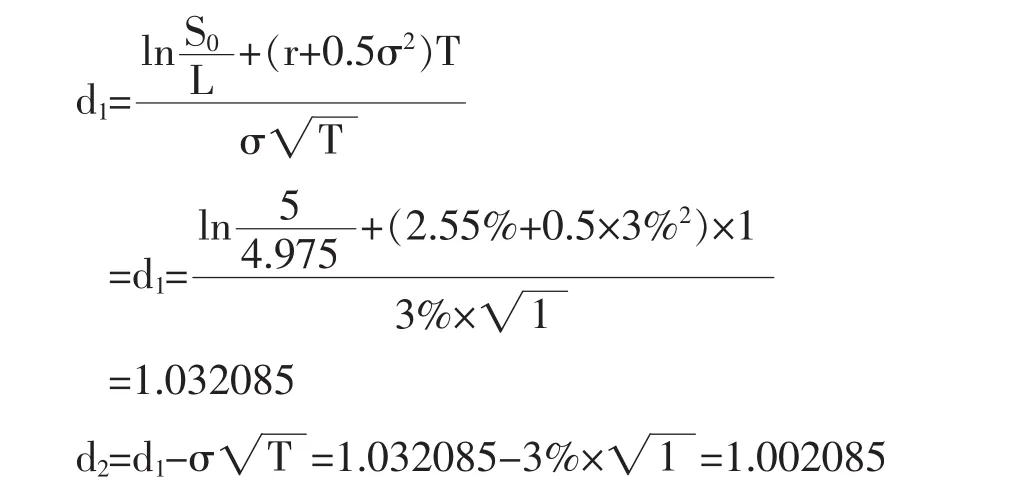
查正态分布表得：N（1-d1）=0.151016，N（1-d2）=0.158151

最后，计算看跌期权的值：

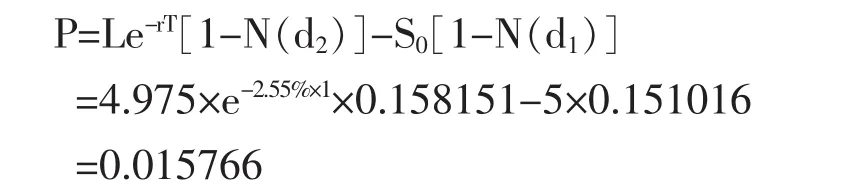
同理，可以利用B-S期权定价模型计算出其他不同情况下看跌期权的价格：

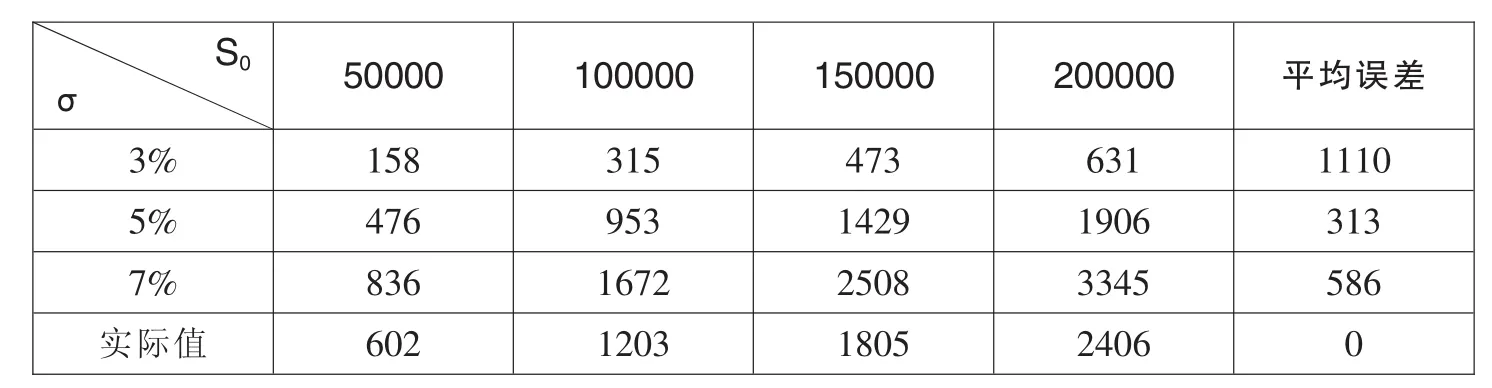
表1 免赔率为5‰时的看跌期权价格表 单位：（元）

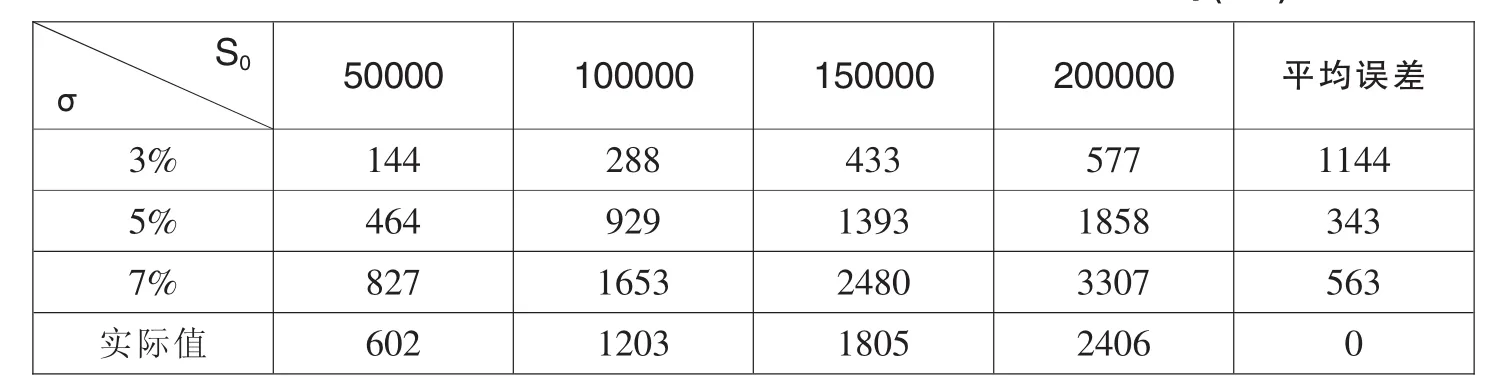
表2 免赔率为10‰时的看跌期权价格表 单位：（元）

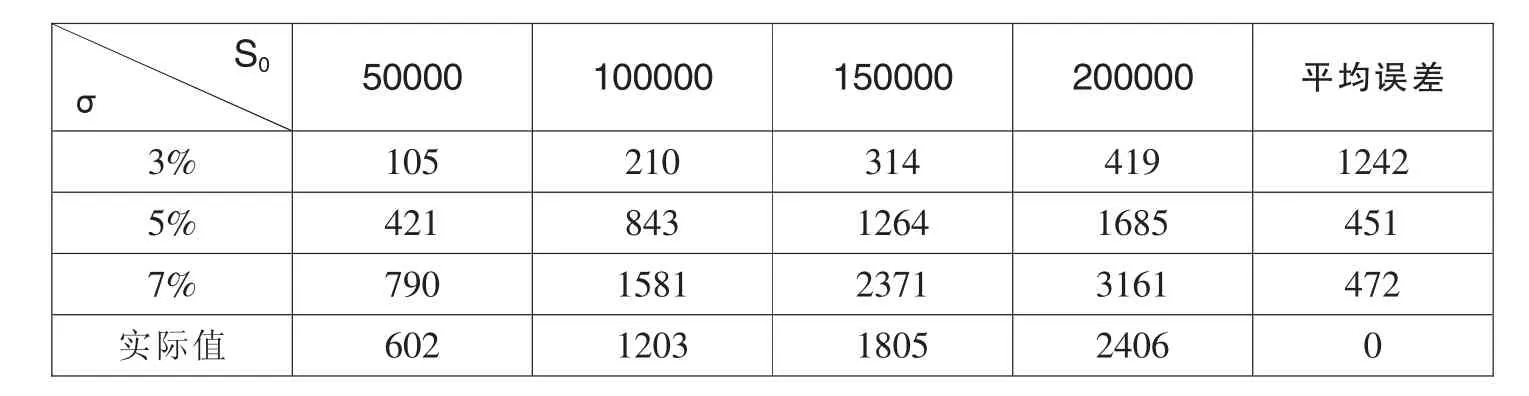
表3 免赔率为20‰时的看跌期权价格表 单位：（元）

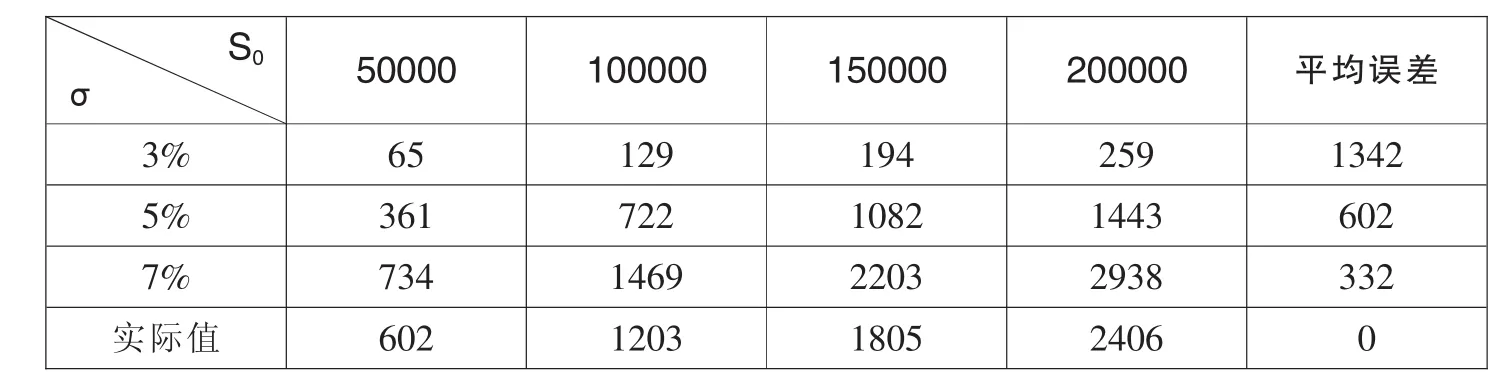
表4 免赔率为30‰时的看跌期权价格表 单位：（元）

通过以上的数据对比，可以得出，当免赔率为5‰和10‰时，此险种的真实值与标的资产的资产波动率为5%的看跌期权价格较为接近；当免赔率为20‰时，此险种的真实值与标的资产的资产波动率为5%和7%的看跌期权价格都比较接近；当免赔率为30‰时，此险种的真实值则较为接近于标的资产的资产波动率为7%的看跌期权价格。据此，我们可以得出，随着免赔率的增加，保险的真实价格越接近于资产波动率越高的看跌期权的价格。

四、拟合度的测量

为了进一步说明利用B-S期权定价模型计算出的期权价格和实际保费之间的关系，下面运用最小二乘法对实际值和计算值进行回归分析。

设实际保费值为Y，利用模型计算出的期权价格为X，当绝对免赔率为5‰，资产波动率为5%时，运用EViews软件可以得出X与Y之间的关系如下：

同理，可以计算出其他情况下X与Y之间的关系：

当免赔率为10‰，σ=7%时，Y=0.500071514+0.7274706319*X（0.399941） （0.000177）

R2=1.000000 DW=2.531467

当免赔率为20‰，σ=7%时，Y=0.5002077015+0.7609767391*X（0.628045） （0.000290）

R2=1.000000 DW=3.014532

当免赔率为30‰，σ=7%时，Y=0.9095859218+0.8186766961*X（0.704211） （0.000350）

R2=1.000000 DW=3.399891

通过以上数据可以看出，利用B-S期权定价模型计算出的期权价格与实际保费之间有着较为明显的线性关系，且这种线性关系与Y=X十分接近，这说明两者之间具有比较好的拟合性，所以，我们可以得出：将B-S期权定价模型运用在财产保险的定价中具有一定的科学性。

五、结 论

由于数据较少，本文只比较分析了一家保险公司的其中的一个险种与计算出的期权价格的关系，但通过以上的分析，可以表明，财产保险的期权定价具有一定的科学性。利用B-S期权定价模型可以衡量财险产品价格的合理性，反推市场变量，为再保险提供思路等［3］。虽然这一方法不可避免地存在一些缺陷，但是保险人仍可以将这一模型灵活地运用在财险定价中，充实和丰富传统的保费定价，为财产保险的定价提供一些新思路。

［1］ 黄昆，吕凡.期权定价模型在财产保险方面的运用［J］.科技信息，2011（25）：5-6.

［2］ 张骋.期权定价在保险中的适用性探讨［J］.中国证券期货，2011（8）：29-30.

［3］ 刘婕.浅谈财产保险的期权定价［J］.时代金融，2008（1）：33-34.