弹性网回归在功能磁共振成像数据分析中的应用综述

吴筱菁

（北京交通大学计算机与信息技术学院，北京 100044）

1 引 言

功能磁共振成像（fMRI）是近年来发展日益成熟的一种脑功能成像方式，其数据分析目标包括定位脑激活区域、确定脑功能网络等，能为评估大脑如何处理认知信息提供有用的线索[1]。由于fMRI数据维度高，一般样本量较小，特征常具有高度共线性[2]，普通分析方法难以得到解释性好的模型。正则化回归能进行稀疏的特征选择，可以较好地适用于fMRI数据，其中弹性网回归[3]是性能比较稳定的一种，Carroll等人[4]的研究表明弹性网回归方法分析fMRI数据能得到优良的预测模型，证明了其可靠性和稳定性。

本文将介绍弹性网回归方法的基本原理，分析其应用在功能磁共振数据分析中的优势，并整理近年其应用情况，最后提出总结和展望。

2 弹性网回归方法及特点介绍

2.1 弹性网回归方法基本原理

对于样本量为N，特征维度为ρ的线性回归模型

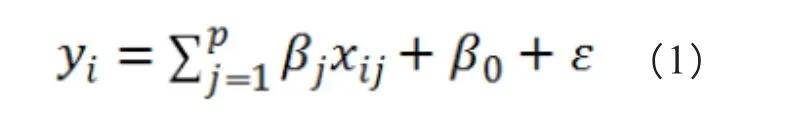
其中ε～N(0,σ2)为误差项，βj为模型的回归系数，i=1,2,…,N, j=1,2,…,р。使用带有弹性网惩罚项的最小二乘法估计模型参数即估计回归系数βj，βo，以使损失函数最小化：

其中，惩罚项为

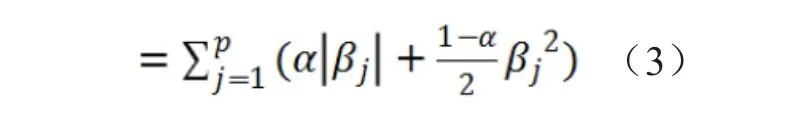
弹性网回归方法的惩罚项由lasso惩罚项（‖β‖1）和岭回归惩罚项（1/2‖β‖2）组成，式（2）中正则化参数 λ 能够调节模型的稀疏程度，λ 值越大，模型稀疏度越大；式（3）中的正则化参数α调节岭回归惩罚项和lasso惩罚项之间的比例，取值范围分别是，λ＞0，α∈[0，1]。

2.2 弹性网回归方法的优点

弹性网回归惩罚项中Lasso用于使许多参数收缩到零值，进而获得稀疏预测模型，并选择一些相互关联的变量包含在模型中，并可应用于预测变量的数目远大于被试数目的情形[5]。岭回归是专用于共线性数据分析的有偏估计回归方法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数的稳定的数值解，将相关预测因子的系数相互收缩，使相关变量的参数具有大致相同的值[6]；

lasso回归未考虑特征之间的关联性，不适用于多重共线性变量；岭回归没有实际系数为零的预测因子，不能进行模型选择[7]；弹性网回归方法将二者结合，通过交叉验证进行特征选择时，可以得到理想的稀疏模型，并补偿观测变量之间的相关性带来的影响。

3 弹性网回归方法在fMRI分析中的应用

3.1 弹性网回归方法在疾病相关研究中的应用

疾病相关的fMRI研究涉及阿尔兹海默症等多种神经系统病变性疾病。弹性网回归用于选择可靠的特征以区分健康人与疾病患者，有助于疾病的辅助诊断。针对阿尔兹海默症，Schoutena等人[7]使用多模式结合方法，利用弹性网分类结合多种磁共振成像，得到阿尔兹海默症患者与健康人的良好分类器。Bowman等人[8]进行了寻找帕金森病早期诊断的相关生物标记的研究，提出一种统计框架以确定可靠的特征区分帕金森患者与健康人。将弹性网惩罚法应用到逻辑斯蒂回归，并引入附加标准，获得了较高的分类准确率。

3.2 弹性网回归方法在认知与脑发育研究中的应用

基于正常人的研究普遍验证了弹性网方法的有效性，为了解人的大脑发育过程及大脑各区域相互作用模式提供了有价值的信息。Mohr等人[9]研究大脑功能定位的整合过程，选取健康成年人进行视觉刺激和响应的任务，基于任务态fMRI数据分别使用弹性网回归、 GraphNet等方法进行稀疏分类任务，为大脑功能定位整合过程的解读提供了新的视角。Tian等人[10]使用健康成年人的静息态fMRI数据，通过弹性网回归方法进行回归预测及分类任务。研究发现人在成年早期至中期，大脑各区域功能相互作用发生了可见的改变，成年中期时大脑的功能已经开始退化。

3.3 弹性网回归方法性能的相关研究

弹性网回归在不同情况下的应用效果一直也是研究者们关心的问题。Wehbe等人[11]通过阅读任务相关的fMRI数据，结合空间平滑方法，比较了弹性网回归等一系列正则化回归方法的预测效果，发现正则化的密度对于识别与任务相关的大脑激活体素的重要作用，且不同正则化方法的使用效果相当，寻求更优分析方法还与建模的谨慎性有所关联。Belilovsky等人[12]利用健康被试和可卡因成瘾被试的任务态fMRI数据，比较了lasso、弹性网及k支持项三种方法的回归预测效果、稳定性及结果可解释性，发现k支持项的回归方法较另两种有更好的预测效果，同时具有优良的计算特性。此外与可卡因成瘾相关的结果和前人的研究相吻合，进而证明了k支持项回归方法的有效性。

3.4 弹性网回归方法的扩展应用

除常规应用之外，研究者们近年来对弹性网回归进行了各种方式的延伸和扩展，取得了不同程度的效果。Lorbert等人[13]基于任务态fMRI使用弹性网正则化的支持向量机进行自动特征选择，证实了该方法在真实的fMRI数据中应用的有效性。Gkirtzou等人[14]针对常规fMRI分析中体素之间关系的编码信息被忽略的问题进行了探究，考虑大脑内在的空间结构，尝试提高功能磁共振图像分析的预测效果。经真实数据的检验，该方法的性能优于岭回归及弹性网回归，同时验证了大脑体素之间的连接包含脑结构的补充信息这一假设。

4 总结与展望

作为一种收缩和选择的方法，弹性网能够产生稀疏的模型，并保证良好的预测准确率，同时鼓励分组效应。已有的实际结果和模拟已广泛的证明，弹性网优于lasso的优越性能，以及在神经影像科学研究中的有效性。分类算法中，弹性网的优良特性能够得到更好地提现。未来弹性网作为一个重要的基础，能得到更多广泛的应用。

[1]Belilovsky E,Gkirtzou K,Misyrlis M,et al.Predictive sparse modeling of fMRI data for improved classi fi cation,regression,and visualization using the k-support norm[J].Computerized Medical Imaging & Graphics,2015,46 Pt 1(1)：40.

[2]Bunea F,She Y,Ombao H,et al.Penalized least squares regression methods and applications to neuroimaging[J].Neuroimage,2011,55(4)：1519-27.

[3]Zou H, Hastie T. Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society：Series B (Statistical Methodolo gy),2005,67(2)：301-320.

[4]Carroll M K,Cecchi G A,Rish I, et al. Prediction and interpretation of distributed neural activity with sparse models[J]. Neuroimage,2009,44(1)：112.

[5]Bunea F, She Y, Ombao H, et al. Penalized least squares regression methods and applications to neuroimaging[J].NeuroImage,2011,55(4)：1519-1527.

[6]Khundrakpam B S,Tohka J,Evans A C. Prediction of brain maturity based on cortical thickness at different spatial resolutions[J].Neuroimage,2015,111：350.

[7]Schouten T M,Koini M,De V F,et al.Combining anatomical,diffusion, and resting state functional magnetic resonance imaging for individual classi fi cation of mild and moderate Alzheimer's disease[J]. Neuroimage Clinical,2016,11：46.

[8]Bowman D B,Drake D F,Huddleston D E.Multimodal Imaging Signatures of Parkinson's Disease[J].Frontiers in Neuroscience,2016,10.

[9]Mohr H,Wolfensteller U,Frimmel S,et al.Sparse regularization techniques provide novel insights into outcome integration processes[J].Neuroimage,2015,104：163-176.

[10]Tian L, Ma L, Wang L. Alterations of functional connectivities from early to middle adulthood：Clues from multivariate pattern analysis of resting state fMRI data[J].Neuroimage,2016,129：389.

[11]Wehbe L, Ramdas A, Steorts R C,et al.Regularized brain reading with shrinkage and smoothing[J].2014,9(4).

[12]Kumawat G, Singh G, Gireesh C,et al.Predictive sparse modeling of fMRI data for improved classification,regression, and visualization using the k -support norm[J].Computerized Medical Imaging & Graphics the Official Journal of the Computerized Medical Imaging Society,2015,46 Pt 1(1)：40.

[13]Lorbert A, RamadgePJ. The Pairwise Elastic Net support vector machine for automatic fMRI feature selection[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2013：1036-1040.

[14]Gkirtzou K,Honorio J,Samaras D,et al.fMRI Analysis with Sparse Weisfeiler-Lehman Graph Statistics[M]//Machine Learning in Medical Imaging.Springer International Publishing,2013：90-97.