基于变分高斯过程模型的快速核偏标记学习算法
2017-02-22贺建军
周 瑜 贺建军,2 顾 宏
1(大连理工大学电子信息与电气工程学部 辽宁大连 116024)2 (大连民族大学信息与通信工程学院 辽宁大连 116600)(yuzhou829@sina.com)
基于变分高斯过程模型的快速核偏标记学习算法
周 瑜1贺建军1,2顾 宏1
1(大连理工大学电子信息与电气工程学部 辽宁大连 116024)2(大连民族大学信息与通信工程学院 辽宁大连 116600)(yuzhou829@sina.com)
偏标记学习(partial label learning)是人们最近提出的一种弱监督机器学习框架,由于放松了训练数据集的构造条件,只需知道训练样本的真实标记的一个候选集合就可进行学习,可以更方便地处理很多领域的实际问题.在该框架下,训练数据的标记信息不再具有单一性和明确性,这就使得学习算法的构建变得比传统分类问题更加困难,目前只建立了几种面向小规模训练数据的学习算法.先利用ECOC技术将原始偏标记训练集转换为若干标准二分类数据集,然后基于变分高斯过程模型在每个二分类数据集上构建一个具有较低计算复杂度的二分类算法,最终实现了一种面向大规模数据的快速核偏标记学习算法.仿真实验结果表明,所提算法在预测精度几乎相当的情况下,训练时间要远远少于已有的核偏标记学习算法,利用普通的PC机处理样本规模达到百万级的问题只需要40 min.
偏标记学习;核方法;大规模数据;高斯过程;分类
在传统分类技术中,通常需要通过一个样本的真实标记信息准确给定的训练数据集来训练分类器,而在很多实际问题中,这种强监督训练数据通常很难或者需要付出很大代价才能获得,相反,具有弱监督标记信息的数据却唾手可得.例如,在医疗诊断中,医生通过一个病人的症状(如关节疼、发烧、血沉高),往往可以判断他得了哪几种疾病(可能是风湿性关节炎、布氏杆菌病或其他疾病),而很难确定具体是哪种疾病;在互联网应用中,用户可以自由地为各种在线对象提供标注,但对象获得的多个标注中可能仅有一个是正确的.因此,如何在弱监督信息条件下有效地进行学习建模已成为了很多领域的共同需求.偏标记集学习(partial label learning[1-3],也称learning from candidate labeling sets[4],ambiguous label learning[5],superset label learning[6])是最近提出的一种重要的弱监督学习框架,主要解决在只知道训练样本的真实标记属于某个候选标记集合的情况下如何进行学习的问题.由于偏标记学习是对传统分类技术的一个扩展,放松了构造训练数据集的条件,因此它与传统分类技术一样具有广阔的应用空间,可以解决图像处理[7]、文本挖掘[8]、医疗诊断[9]等领域的各种实际问题.
在偏标记学习框架下,所能利用的训练数据的标记信息不再具有单一性和明确性,真实标记湮没于候选标记集合中,这就使得学习算法的构建变得比传统分类算法更加困难.最早的偏标记学习算法可以追溯到2002年Grandvalet[10]对Logistic回归模型的拓展研究,随后Jin 和 Ghahramani[11]将偏标记学习归结为一种新的机器学习框架,提出了基于辨识模型的学习算法.在这2组科研人员的早期工作推动下,偏标记学习逐渐引起人们的关注,尝试将传统的机器学习模型引入偏标记学习算法的构建问题中,文献[5]提出了一种基于k近邻方法的偏标记学习算法;文献[12]提出了基于最大似然估计和信度函数的学习算法;Luo 和 Orabona[4]提出了最大间隔偏标记学习算法;Cour 等人[2]和Nguyen等人[13]分别提出了线性支持向量机偏标记学习算法;Liu和Dietterich[6]提出了条件混合多变量模型;Zhang[3]利用纠错输出编码技术(ECOC)提出了一种基于集成分类器的偏标记学习算法;文献[14]提出了一种针对结构化输入数据的偏标记学习算法;文献[15]提出了一种基于加权图模型的算法.虽然经过人们不断的努力,目前已经出现了CLPL[2],PL-ECOC[3],IPAL[15]等几种较有效的偏标记学习算法,但是这些算法要么计算复杂度较高不易处理大规模数据,要么是线性算法不易处理非线性问题,几乎都不能有效处理大规模非线性偏标记学习问题.针对以上问题,本文将结合纠错输出编码技术和变分高斯过程模型建立一种快速核偏标记学习算法,与PL-ECOC[3]等基于核方法的偏标记学习算法相比,本文算法的计算速度要远远快于这些算法,与CLPL[2]等线性偏标记学习算法相比,本文算法的精度要高于这些算法.
1 算法描述
设X为样本的特征空间,Y={y1,y2,…,yQ}为类别标记集合.偏标记学习的目的是利用一个训练集S={(x1,Y1),(x2,Y2),…,(xn,Yn)}(其中xi∈X是样本的特征向量;Yi≡{yi1,yi2,…,yini}⊂Y是样本xi的真实标记的一个候选集合)确定一个函数f:X→Y,使得f可以正确输出新(待预测)样本x*∈X的类别标记.可以看出,与传统分类框架明确给定每个训练样本的真实标记不同,在偏标记学习框架下,我们只知道训练数据的真实标记属于某一个候选集合.为了设计有效的偏标记学习算法,一种直观的思路是通过定义新的模型损失函数来实现对偏标记数据的候选标记集合进行消歧,然而,该类算法常常会受到伪标记带来的不利影响[1].最近,文献[3]提出了一种非消歧策略,基本思想是利用ECOC技术将偏标记学习问题的训练数据集变换为具有确切标记信息的多个二分类问题的数据集,然后在每个二分类数据集上建立一个标准的二分类器,最后将各个分类器的结果综合来输出预测结果.本文也将基于以上策略,先利用ECOC技术将问题转换为二分类问题,然后采用变分高斯过程二分类算法来实现最终的快速核偏标记学习算法.虽然都是基于ECOC技术来构建偏标记学习算法,本文和文献[3]的研究重点和创新性是不同的,文献[3]的重点是构建一种基于非消歧策略的偏标记学习算法,主要创新是将ECOC技术引入到了偏标记学习问题中;而本文的重点是构建一种面向大规模数据的偏标记学习算法,主要创新在采用了适合该问题的二分类器.下面分别对基于ECOC技术的问题变换策略和类不平衡变分高斯过程二分类器这2个本文算法的核心模块进行描述.
1.1 基于ECOC技术的问题变换策略

(1)
假设fl:X→{+1,-1}是基于训练集Sl构建的二分类器,F*=(f1(x*),f2(x*),…,fL(x*))是由各个二分类器在待预测样本x*上的输出构成的向量,在解码阶段可以将码字与F*最接近的类别作为待预测样本的类别,即
(2)
其中,dist(·)表示2个向量之间的距离,本文将采用海明距离.
1.2 类不平衡变分高斯过程二分类器
由于通过ECOC技术变换得到的二分类数据集有时是一种类不平衡数据集,即正负类样本数目的比例会很悬殊,特别是当原始偏标记训练数据集本身存在类不平衡问题时,上述现象更为明显,因此构建的二分类器需要能很好地处理类不平衡问题.另外,我们希望构建一种面向大规模数据的非线性算法,因此二分类器最好是一种具有较低计算复杂度的核分类算法.虽然人们已经就面向大规模数据的核机器学习技术开展了一系列的研究,但是符合以上条件的算法并不多.KLSP算法[16]是一种基于变分原理建立的面向大规模数据的高斯过程二分类算法,它不仅具有较低的计算复杂度和较高的精度,而且还具有避免过拟合、可以用分布式或者随机优化的方法对模型进行求解等优点,但是该算法并不能处理类不平衡问题,本节将采用一种改进的KLSP算法来作为本文算法的二分类器.
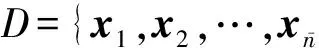
1) 假设f(x)服从如下零均值高斯过程分布:
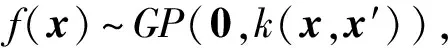
(3)
其中,k(x,x′)表示协方差函数,本文将使用RBF核α1e-‖x-x′‖2α2作为协方差函数.利用式(3),可以得到f(x)在训练样本集D上的函数值FD的先验概率分布p(FD|D)=N(FD|0,KD),以及f(x)在待预测样本x*上的函数值f*=f(x*)关于FD的条件先验概率分布p(f*|FD,x*,D)=N(f*|K*D,其中FD=(f1,f2,…,=f(xi),KD是协方差函数k(x,x′)在样本集D上的值构成的方阵,K*D表示预测样本x*和D中样本之间的协方差函数值构成的行向量,K*=k(x*,x*).
2) 定义联合似然函数
(4)
其中,p(yi|fi)可以利用Logistic函数定义为p(yi|fi)=1(1+e-yifi).
3) 计算FD的后验概率分布:
(5)
由于不能得到p(FD|D,Y)的分析表达式,通常需要利用Laplace逼近[16]、Expectation Propagation[17]等方法计算它的一个近似表达式q(FD|D,Y).
4) 根据p(FD|D,Y)和p(f*|FD,D,x*)计算f*的后验概率:
p(f*|D,Y,x*)=
(6)
从而得到x*是正样本的概率为
p(y*=+1|D,Y,x*)=
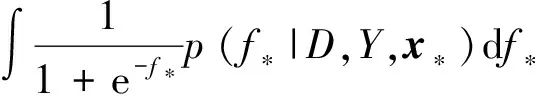
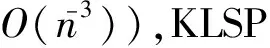
p(FD|D,Y)=∫p(FD|FU,D)p(FU|D,Y)dFU≈
(7)
其中,FU是潜变量函数f(x)在训练样本集D的一个子集U(U的选取方式见算法实现部分)上的函数值,即FU=(f(xi1),f(xi2),…,f(xim))T,xim∈U,而q(FU|D,Y)=N(FU|μ,Σ)可以通过最大化边缘似然p(Y|D)的下界得到:
lnp(Y|D)=ln ∫p(Y|FU)p(FU|D)dFU≥
∫∫lnp(Y|FD)p(FD|FU,D)q(FU|D,Y)dFUdFD-
KL(q(FU|D,Y)‖p(FU|D))Ψ(μ,Σ).
(8)
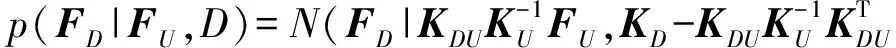
在得到由式(7)表示的后验概率分布p(FD|D,Y)后,后验概率分布式(6)可以重新表示为
p(f*|D,Y,x*)=
∫p(f*|FD,D,x*)p(FD|D,Y)dFD≈
∫p(f*|FD,D,x*)∫p(FD|FU,D)q(FU|D,

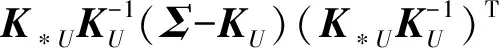
(9)
从式(9)可以看出,f*的后验概率分布主要与子集U和q(FU|D,Y)=N(FU|μ,Σ)有关,因此算法的主要计算量来自计算q(FU|D,Y)=N(FU|μ,Σ).
由于通过ECOC技术变换得到的二分类数据集有时是类不平衡数据集,而前面描述的变分高斯过程分类算法KLSP并不能处理类不平衡问题.我们可以通过定义改进的联合似然函数来实现处理不平衡问题的目的,即在联合似然函数中的正负类样本对应的似然上引入不同的权重系数,使得错分少数类样本的代价大于错分多数类样本的代价,最终实现改善少数类样本预测精度的目的.按照该思想,可以将式(4)定义的联合似然函数重新定义为
(10)
(11)
对Ψ(μ,Σ)分别关于μ,Σ求导,可得:
(12)

在得到梯度式(12)后,可以采用各种基于梯度的优化方法求解μ,Σ.求得μ,Σ以后就可以利用式(9)计算f*的后验概率分布,从而得到样本x*是正样本的概率为
p(y*=+1|D,Y,x*)=
(13)
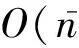
2 算法实现
本文算法的流程图如算法1所示,下面给出各个关键模块的实施细节.诱导子集U可以通过各种聚类算法来选取,为了减少计算时间,本文采用Chen[18]实现的一种快速K均值聚类算法来完成U的(假设包含m个样本)选取.基本规则是先对正负类样本分别进行聚类各生成m2个聚类中心,然后把这些聚类中心合并来构成U.在算法的训练和预测阶段都需要频繁地用到协方差矩阵KU的逆矩阵,而在有的实际问题中KU会是一个奇异矩阵,为了保证数值稳定性,在计算KU的逆矩阵时我们加入了一个扰动项10-7I,即=(KU+10-7I)-1.通过权衡计算复杂度、存储复杂度和稳定性等因素,本文采用了有限储存拟牛顿方法(L-BFGS)来计算潜变量函数FU的均值和方差μ,Σ,L-BFGS算法的详细计算流程本文将不再赘述,可以参见文献[19].
算法1. PL-ECOC-VGP算法的伪代码.
训练阶段.
输入:训练集S、ECOC的编码长度L、诱导集的样本个数m、L-BFGS算法的存储长度M、二分类集的最少样本个数thr、L-BFGS算法的迭代次数iter、协方差函数的参数α1和α2;

forl=1,2,…,Ldo
1) 生成编码矩阵M的第l行元素,构造第l个二分类训练集Sl=∅:
① 随机生成一个长度为Q的二值编码向量v∈{-1,+1}Q;
② 根据式(2)构造二分类训练集Sl;
③ 如果|Sl| ④ 设定编码矩阵M的第l行元素为v,即M(l,:)=v; 2) 以Sl为训练数据集构造变分高斯过程分类器fl: ① 利用快速聚类算法[18]选取诱导子集U; ③ 根据式(12)利用L-BFGS算法[19]计算FU的均值μ和方差Σ,其中L-BFGS算法的迭代次数设定为iter,存储长度设定为M; end for 预测阶段. 输出:x*的预测类别. ① 计算K*; ② forl=1,2,…,Ldo ③ 计算Ul与x*的协方差矩阵K*Ul; ⑤ 如果p(y*=+1|D,Y,x*)>0.5,则确定fl在x*的输出为fl(x*)=+1,否则fl(x*)=-1; ⑥ end for ⑦ 根据式(2)确定算法对x*的预测类别. 为了验证本文所建算法(简记为PL-ECOC-VGP)的性能,本节将其与CLPL[2]和PL-ECOC[3]2个代表性的偏标记学习算法在6个UCI数据集[20]上进行了比较,其中CLPL算法是2011年由Cour等人建立的一种线性偏标记学习算法,PL-ECOC算法是2014年由Zhang建立的一种核偏标记学习算法.这些UCI数据集的样本数目从1万~100万量级不等,详细信息如表1所示.由于UCI数据集是标准的传统分类数据集,我们采用了2个控制参数p,r来把它们变换为偏标记数据集,其中p表示偏标记样本(即|Yi|>1)在整个样本集中的比例,r表示偏标记样本的除真实标记以外的候选标记个数,即r=|Yi|-1.变换过程如下:对于给定的每一对参数(p,r),先从原始的UCI数据集中随机选取pn个样本(n为样本总数);然后对于每一个被选取的样本,随机地从它的真实标记以外的类别标记中选取r个与真实标记一起构成该样本的候选标记.以下的所有实验结果都是通过随机选取12的样本作为训练数据,12的样本作为测试数据,然后重复进行5次实验得到的平均结果.所有结果都是在CPU主频为2.5 GHz、内存为8 GB的笔记本电脑上运行得到的. Table 1 The UCI Data Sets for Validating the Performanceof the Proposed Algorithm 观察算法流程图可以看出,PL-ECOC-VGP算法的参数比较多,为了避免参数选择的麻烦,我们首先在Shuttle数据集(控制参数为p=0.6,r=3)和Protein数据集(控制参数为p=0.6,r=1)上观察了这些参数取不同值时对算法性能的影响;然后对于一些对算法精度影响不是太大的参数,在所有的数据集上都设定了统一的参数,如L-BFGS算法的迭代次数iter和记忆存储长度M都默认地设定为5,设定ECOC的编码长度L=10 lnQ,设定二分类集的最少样本个数thr=n10.协方差函数的参数α1和α2的取值对算法精度的影响比较大,考虑到在连续的数值点上选取最优参数比较费时,在每个数据集上α1和α2的取值是在一个离散点集{(α1,α2)|α1=10-4,10-3,…,104;α2=3-2d,3-1d,…,32d}(d为随机选取7 000个训练样本计算得到的样本之间的平均距离)上利用交叉验证法选取得到的.对于诱导子集的样本个数m,我们发现在Shuttle数据集和Protein数据集上出现了2种完全不同的变化规律.如图1所示,在Protein数据集上,随着m取值的变大则算法的预测精度会逐渐变高;而在Shuttle数据集上却正好相反,算法的预测精度会随着m取值的变大而逐渐变低.通过进一步分析我们发现,这可能与训练样本的特征维数有关,在Shuttle数据集中样本的特征维数是9,而在Protein数据集中样本的特征维数为357.为了验证这个猜测在其他的数据集上做了验证,发现以上猜测基本是正确的,当样本的特征维数比较高时,需要的诱导样本个数也比较多,但是这二者之间没有固定的比例,而且当m的取值变大时算法的计算时间会增加.因此在下面的实验中,对于特征维数在10左右的数据集,m的取值统一设定为50;对于剩下的数据集,m的取值统一设定为250. Fig. 1 The accuracy of PL-ECOC-VGP algorithm when varying the number of inducing samples图1 m取不同值时PL-ECOC-VGP算法的预测精度 表2列出了PL-ECOC-VGP,CLPL,PL-ECOC 3个算法在各个控制数据集上的性能表现,包括Acc,mAcc,Time三个性能指标,其中,Acc表示算法在整体数据集的预测精度,mAcc表示算法在数据集的各个类别上的预测精度的平均值,Time表示算法的训练时间(单位为s).CLPL,PL-ECOC算法的代码是直接从相关作者的个人主页上下载的,参数是按照原文提供的方法设定的.从表2可以看出,虽然CLPL算法的训练时间要远远小于其他2个算法,但是它的预测精度也明显比其他2个算法差.就本文提出的PL-ECOC-VGP算法和文献[3]的PL-ECOC算法这2种核方法相比,它们的预测精度几乎相当,但是PL-ECOC-VGP算法的训练时间要远远小于PL-ECOC算法,对于特征维数较低而样本数目较大的数据集(如Shuttle,Poker-hand),这种优势会越明显.另外,对于大部分数据集,在性能指标mAcc上PL-ECOC-VGP算法的结果要优于PL-ECOC算法,而在性能指标Acc上PL-ECOC算法的结果要优于PL-ECOC-VGP算法.由于Acc指标反映的是整体数据集上的精度,而mAcc指标可以反映出每个类别上的预测精度,这表明,PL-ECOC-VGP算法侧重在各个类别上取得较好的精度,而PL-ECOC算法侧重在整体数据集上取得较好的精度.换句话说,与PL-ECOC算法相比,PL-ECOC-VGP算法能更好地处理类不平衡问题,这主要是源于我们构建的不平衡高斯过程二分类器. Table 2 The Performance Comparison of Three Partial Label Learning Algorithms on UCI Data Sets 本文基于ECOC技术和人们最近提出的变分高斯过程模型建立了一种面向大规模偏标记学习问题的快速核分类算法,在6个UCI数据集上的实验结果表明,本文算法的训练时间要明显少于其他核偏标记学习算法.当然,与已有的线性偏标记学习算法相比,本文算法的训练时间还是较长,这主要是由于算法需要训练多个高斯过程二分类器.下一步将尝试通过定义新的模型损失函数的方式来建立面向偏标记问题的变分高斯过程算法,这种策略虽然可能会受到伪标记带来的不利影响,但是由于只需要训练一个分类器,因此计算时间会极大地降低.此外,目前选取协方差函数参数和诱导子集样本个数的策略不仅效率低而且不能得到最优参数,如何利用模型的边缘似然自动选择这些参数也是下一步需要考虑的问题. [1]Zhang Minling. Research on partial label learning [J]. Journal of Data Acquisition & Processing, 2015, 30(1): 77-87 (in Chinese)(张敏灵. 偏标记学习研究综述[J]. 数据采集与处理, 2015, 30(1): 77-87) [2]Cour T, Sapp B, Taskar B. Learning from partial labels [J]. Journal of Machine Learning Research, 2011, 12: 1501-1536 [3]Zhang M. Disambiguation-free partial label learning [C]Proc of the 14th SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2014: 37-45 [4]Luo J, Orabona F. Learning from candidate labeling sets [C]Advances in Neural Information Processing Systems. Montreal, Canada: Neural Information Processing System Foundation, 2010: 1504-1512 [5]Hüllermeier E, Beringer J. Learning from ambiguously labeled examples[J]. Intelligent Data Analysis, 2006, 10(5): 419-439 [6]Liu L, Dietterich T. A conditional multinomial mixture model for superset label learning [C]Advances in Neural Information Processing Systems. Montreal, Canada: Neural Information Processing System Foundation, 2012: 557-565 [7]Zeng Z, Xiao S, Jia K, et al. Learning by associating ambiguously labeled images[C]Proc of the 26th IEEE Int Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2013: 708-715 [8]Grandvalet Y, Bengio Y. Learning from partial labels with minimum entropy, 2004s-28[R]. Montreal, Canada: Center for Interuniversity Research and Analysis of Organizations, 2004 [9]Fung G, Dundar M, Krishnapuram B, et al. Multiple instance learning for computer aided diagnosis [C]Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2007: 425-432 [10]Grandvalet Y. Logistic regression for partial labels [C]Proc of the 9th Int Conf on Information Processing and Management of Uncertainty in Knowledge-Based Systems. Annecy, France: Institute for the Physics and Mathematics of the Universe, 2002: 1935-1941 [11]Jin R, Ghahramani Z. Learning with multiple labels[C]Advances in Neural Information Processing Systems. Montreal, Canada: Neural Information Processing System Foundation, 2002: 897-904 [13]Nguyen N, Caruana R. Classification with partial labels[C]Proc of the 14th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2008: 381-389 [14]Li Chengtao, Zhang Jianwen, Chen Zheng. Structured output learning with candidate labels for local parts[G]LNCS 8189: Proc of the European Conf on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECMLPKDD 2013). Berlin: Springer, 2013: 336-352 [15]Zhang Minling, Yu Fei. Solving the partial label learning problem: An instance-based approach[C]Proc of the 24th Int Joint Conf on Artificial Intelligence (IJCAI’15). Menlo Park, CA: AAAI, 2015: 4048-4054 [16]Williams C, Barber D. Bayesian classification with Gaussian processes[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1998, 20(12): 1342-1351 [17]Kim H, Ghahramani Z. Bayesian Gaussian process classification with the EM-EP algorithm[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2006, 28(12): 1948-1959 [18]Chen M. Kmeans clustering[OL].[2015-08-10]. http:www.mathworks.commatlabcentralfileexchange24616-kmeans-clustering [19]Nocedal J, Wright S. Numerical Optimization[M]. 2nd ed. Berlin: Springer, 1999: 195-204 [20]Bache K, Lichman M. UCI machine learning repository[OL]. 2013 [2015-08-10]. http:archive.ics.uci.eduml Zhou Yu, born in 1982. PhD candidate. Her main research interests include machine learning and data mining. He Jianjun, born in 1983. PhD and associate professor. His main research interests include machine learning and pattern recognition. Gu Hong, born in 1961. Professor and PhD supervisor. His main research interests include machine learning, big data and bioinformatics. Fast Kernel-Based Partial Label Learning Algorithm Based on Variational Gaussian Process ModelZhou Yu1, He Jianjun1,2, and Gu Hong1 1(FacultyofElectronicInformationandElectricalEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024)2(CollegeofInformationandCommunicationEngineering,DalianMinzuUniversity,Dalian,Liaoning116600) Partial label learning is a weakly-supervised machine learning framework proposed recently. Since it loosens the requirement to training data set, i.e. the learning model can be obtained when each training example is only associated with a candidate set of the ground-truth labels, and partial label learning framework can be used to deal with many real-world tasks more conveniently. The ambiguity in training data inevitably makes partial label learning problem more difficult to be addressed than traditional classification problem, and only several algorithms for small-scale training set are available up to the present. Based on ECOC technology and variational Gaussian process model, this paper presents a fast kernel-based partial label learning algorithm which can deal with large-scale problem effectively. The basic strategy is to convert the original training data set into several standard two-class data sets by using ECOC technology firstly, and then to develop a binary classify with lower computational complexity on each two-class data set by using variational Gaussian process model. The experimental results show that the proposed algorithm can achieve almost the same accuracy as the existing state-of-the-art kernel-based partial label learning algorithms but use shorter computing time. More specifically, the proposed algorithm can deal with the problems with millions samples within 40 minutes on a personal computer. partial label learning; kernel method; large-scale data; Gaussian process; classification 2015-09-01; 2016-04-28 国家自然科学基金项目(61503058,61502074,U1560102);辽宁省自然科学基金项目(201602190);中央高校基本科研业务费专项资金项目(DC201501055,DC201501060201) This work was supported by the National Natural Science Foundation of China (61503058,61502074,U1560102), the Natural Science Foundation of Liaoning Province of China (201602190), and the Fundamental Research Funds for the Central Universities (DC201501055, DC201501060201). 顾宏(guhong@dlut.edu.cn) TP391
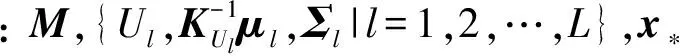
3 仿真实验
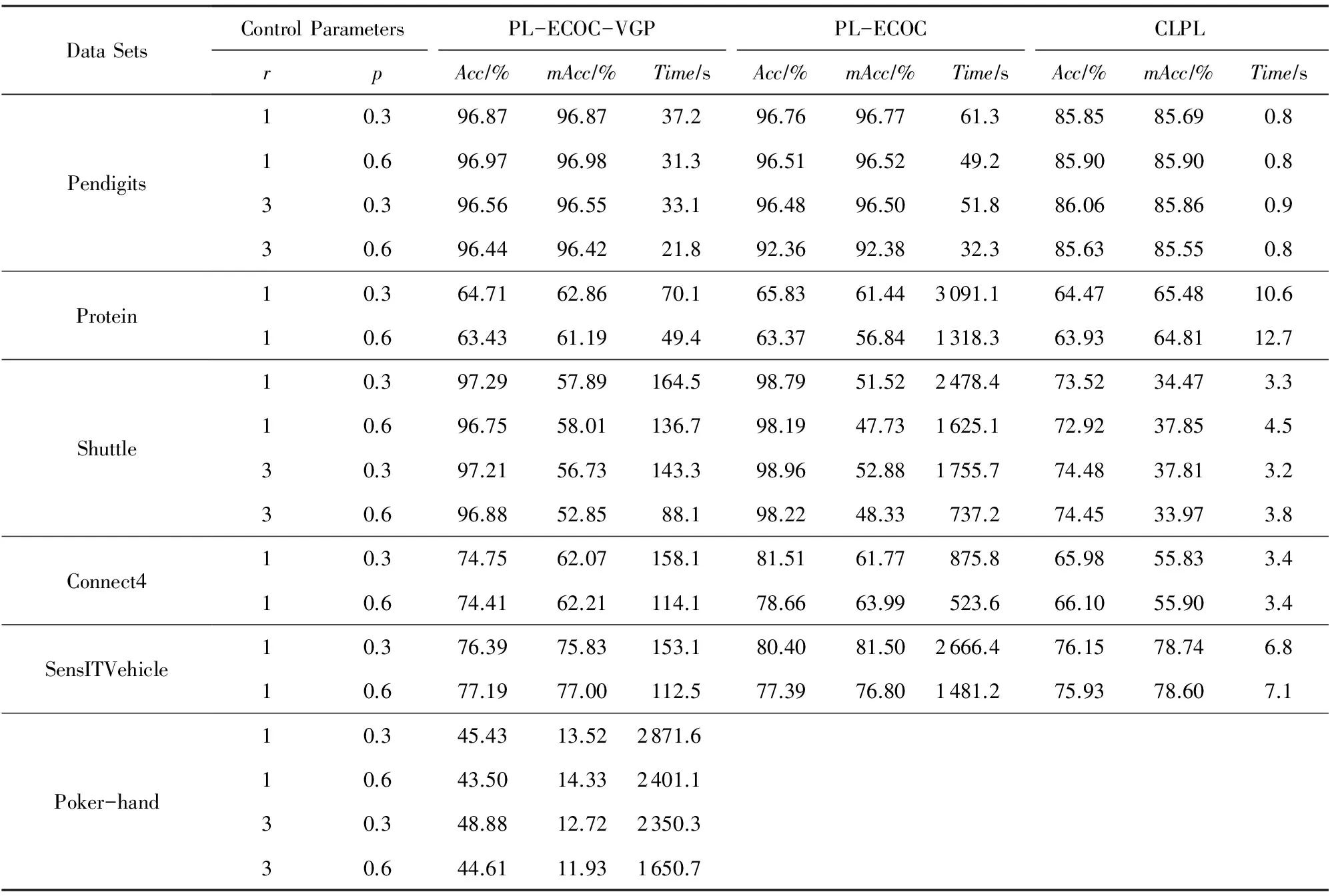
4 结束语



