基于复合结构的知识库分类体系匹配方法

林海伦 贾岩涛 王元卓 靳小龙 程学旗 王伟平

1(中国科学院信息工程研究所 北京 100093)2 (中国科学院网络数据科学与技术重点实验室(中国科学院计算技术研究所) 北京 100190)(linhailun@iie.ac.cn)

基于复合结构的知识库分类体系匹配方法

林海伦1贾岩涛2王元卓2靳小龙2程学旗2王伟平1

1(中国科学院信息工程研究所 北京 100093)2(中国科学院网络数据科学与技术重点实验室(中国科学院计算技术研究所) 北京 100190)(linhailun@iie.ac.cn)

近年来，分类体系匹配由于其在知识库构建和融合等方面的广泛应用，已成为国内外工业界和学术界的研究热点.然而，随着网络大数据的不断发展，分类体系变得越来越庞大和复杂，构造一种通用有效的分类体系匹配器以适应大规模、异构分类体系匹配的扩展性仍然面临很大的挑战.为此，提出了一种基于复合结构的分类体系匹配方法BiMWM，该方法利用分类体系中分类的复合结构信息：微观结构和宏观结构，将分类体系匹配问题转化为二部图上的优化问题进行求解.首先，创建赋权的二部图建模分类体系之间候选的匹配类对关系；然后，通过计算二部图上的最大权匹配剪枝选择最优的分类体系的匹配类对.BiMWM方法可以在多项式时间内为2个分类体系产生最优匹配.实验结果表明:与当前先进的基准方法相比，该方法能够有效提升大规模、异构分类体系匹配的性能.

知识库；分类体系匹配；复合结构；二部图；最大权匹配

知识库是包含实体、关系和分类等的知识集合，而分类体系作为知识库的骨架结构，是知识库中用于语义分类或标注知识项的分类集合.由于不同的知识库可能会包含重叠或互补的数据，已经有越来越多的工作开始尝试通过匹配不同知识库中的公共元素来将它们进行融合.因此，分类体系匹配被认为是知识库融合所需要的最重要的操作之一，其主要任务就是在不同知识库中发现对齐分类体系中共同的元素，从而将描述知识的2个分类体系进行集成，完成2个知识库的融合，实现知识的复用和共享.

特别是近年来，随着知识库取得的成功，如Freebase[1]，YAGO[2]，Probase[3]，Knowledge Graph*https:en.wikipedia.orgwikiEdit_distance等，分类体系匹配问题得到广泛的研究，已有很多研究工作，如RiMOM[4]，PARIS[5]，SiGMa[6]，YAGO+F[7]等.这些研究工作大部分是利用分类自身的信息来计算2个分类体系之间元素的相似度，例如分类的名称、属性或与分类相关的实例以及分类在分类体系中的上下位关系等.然而，目前大部分工作还只能在特定领域发挥作用，而且无法有效地处理大规模的分类体系[8].导致这一问题的原因在于：不同的分类体系通常使用不同的词汇和层级结构来表示自己的分类，而且其对应的可能的匹配空间随分类体系中分类的规模的增加呈现指数级增长.特别是，随着网络大数据[9]的发展，分类体系变得越来越庞大和复杂.基于贪心的方法对处理大规模的分类体系匹配任务可能是一种有效的方法，但由于其贪心的性质，它在匹配决策时难以修正之前的错误.因此，该方法无法保证2个分类体系获得全局最优的匹配.

为了解决上述问题，本文提出了一种基于复合结构的分类体系匹配方法，该方法的设计原理来源于分类体系在结构上具有很多共同点：虽然不同的分类体系具有不同的组织形式，但是分类体系中每一个分类都有标识它的名称、属性、上下文描述以及与该分类相关的实例等；除此之外，还有其在分类体系中的父类、子类和兄弟节点等，我们分别称之为分类的微观结构和宏观结构.因此，很容易得出一个结论：2个分类的微观结构和宏观结构越相似，它们越有可能是在语义上彼此等价的2个分类.因此，本文提出的基于复合结构的方法则基于分类的微观结构和宏观结构特征，将分类体系匹配问题建模为二部图上的优化问题进行求解，通过在二部图模型上执行最大权匹配算法剪枝选择2个分类体系之间可能的候选匹配类对，产生2个分类体系之间的全局最优匹配，从而从整体上提升分类匹配的准确率.创新之处在于：

1) 将异构的分类体系转化为以分类为中心的结构表示，充分利用分类体系中分类之间的关系结构.这里分类的复合结构包括分类体系中分类的微观结构和宏观结构信息.

2) 基于以分类为中心的分类体系结构表示，将分类体系匹配问题建模为二部图上的优化问题，提出了二部图最大权匹配(bipartite maximum weight matching, BiMWM)算法，从而获得2个分类体系之间的全局最优匹配.

1 相关工作

分类体系匹配问题的根源来自于记录链接、重复检测或共指消解问题[10-11].此外，该问题也与模式匹配问题类似.目前，Shvaiko等人[12]对已有的模式匹配工作进行了研究分析，这些工作可分为3类：基于相似度的方法、基于统计的方法和基于复合的方法.这些工作的目标是试图为多个数据源建立一个共同的模式或找到不同模式之间内在的关联方式.

尽管模式匹配问题与分类体系匹配问题类似，但是与模式匹配相比，分类体系匹配有着自己独特的特点：1)与数据模式相比，分类体系在定义数据时提供更高的灵活性和更明确的语义信息；2)数据模式通常是为特定数据库定义的，而分类体系本质上是可重用共享的；3)在分类体系中，知识表示的基本元素的数量更大、更复杂，如传递性、分类不相交性和类型检查约束等.因此模式匹配的方法无法直接适用于分类体系匹配问题.

近年来，分类匹配问题特别是在本体匹配[13]的概念下已被广泛研究.Shvaiko等人[14-15]对已有的分类匹配工作进行了研究分析，目前已有的分类匹配工作根据使用策略的不同可分为5类：

1) 利用分类在分类体系中的指代形式(词汇表示)的策略.这种策略主要基于编辑距离①或Jaccard系数*https:en.wikipedia.orgwikiJaccard_index计算分类名称之间的文本相似度判断分类之间的等价关系，这种策略计算简单、直接.然而，这种策略完全取决于分类的词汇表示，难以区分分类同义和多义表达的情况.

2) 利用语义词典的策略.这种策略主要利用语义词典的信息丰富分类体系中分类的背景信息，如Chen等人[16]利用WordNet的Synset信息扩展分类的同义词信息，提出了一种结合模糊理论与形式概念分析的分类匹配方法FFCA.这种策略受限于词典的覆盖率，当词典中词语缺失时则无法有效工作.

3) 利用分类在分类体系中的上下位关系的策略.这种策略利用分类在分类体系中的近邻结构计算2个分类之间的等价关系，如Li等人[4]提出了一种动态组合策略框架RiMOM，该框架基于2个评估因素：词汇相似度和结构相似度，自动选择分类匹配使用的策略.RiMOM通过在2个分类体系关系图上采用Similarity Flooding技术，提高结构信息对分类匹配的影响.这种策略适用于分类结构相似程度高的分类体系之间的匹配.

4) 利用分类下包含的实例信息的策略.这种策略利用分类包含的实例的重叠率计算分类之间的等价关系，如Suchanek等人[5]提出了一种基于实例的概率化的方法PARIS，该方法通过不同的修剪启发式规则的稀疏表示(特别是在每一步保持分类体系中每个元素的最大分配)来处理维护所有分类匹配的可扩展性问题.Demidova等人[7]采用基于实例的方法将YAGO和Freebase对应的分类体系进行匹配，形成新的YAGO+F知识库.这种策略适用于分类下实例丰富且重叠率高的分类体系之间的匹配.

5) 利用上述信息组合形式的混合策略.如Ba等人[17]利用词汇和实例信息计算分类之间的相似度，基于本体服务器设计开发了一个面向生物医学领域本体匹配的系统ServOMap.Jiménez-Ruiz等人[18]结合词汇相似度、语义相似度和结构相似度计算分类体系中共同的元素，设计开发了LogMap系统.Lacoste-Julien等人[6]针对大规模分类体系提出了一种基于贪心的分类匹配方法SiGMa，该方法组合词汇、属性和结构信息以贪婪的局部搜索的方式发现匹配的分类.基于贪心的方法对处理大规模的分类体系匹配任务来说可能是一种有效的方法.然而，由于其贪心的性质，它在决策时无法修正之前的错误.因此，基于贪心的方法不能保证为2个分类体系获得全局最优的匹配.除上述策略以外，Li等人[19]提出了一种基于用户反馈的分类体系匹配策略，这种策略虽然通过与用户的交互可以提高分类体系匹配的准确率，但是这对用户提出了具备较强的专业知识的能力，难以适用于大规模分类体系的匹配问题.

通过上述分析可以看出，现有的分类体系匹配的工作大部分是通过计算2个分类体系之间的元素相似度来实现的，虽然目前已经构建了很多分类体系匹配器，但是这些匹配器无法有效地处理大规模的分类体系.不仅如此，它们中没有一个主导性的分类体系匹配器能够在所有应用领域都表现得很好.特别是，由于网络大数据的爆炸性增长，分类体系变得越来越庞大和复杂.因此，需要研究新的分类体系匹配方法以便最大程度提升分类体系匹配的有效性.

2 问题定义

本节将详细介绍基于复合结构的分类体系匹配的方法.为此，我们首先描述分类体系的概念，然后给出2个分类体系之间分类一一映射的问题定义.

Suchanek等人[5]把一个分类体系定义为一组形式化的知识集合，包括分类、关系和实例及断言等;Gruber[20]将分类体系定义为是一个形式化的、对于共享概念体系的明确而又详细的说明.由于网络大数据的爆炸性增长，新的知识每天都在不断涌现，因此，现有知识库需要随时间不断演化和改变，所以，知识库的分类体系也不是一成不变的，它应该随着时间进行演化.而开放知识网络[21](open knowledge network, OpenKN)是一个异质的具有时空演化特性的网络，网络中的点和边都具有时间跨度和空间约束来定位以跟踪知识的演化过程.因此，在开放知识网络的概念下，本文把分类体系定义为演化知识网络的模式网络(schema network)，是一个在知识网络中用于语义分类或标注知识项的分类集合.更准确地说，一个分类体系T由4个部分组成：

T=(VT,ET,θ,ψ)，

其中，VT是顶点集合；ET是标记的边的集合；θ:VT→A是定义在顶点上的顶点类型映射函数，满足每个顶点被分配1个唯一的类型θ(v)∈A;ψ:ET→R是定义在顶点对上的关系类型映射函数，满足每对顶点最多被分配给1个关系.

在1个分类体系中，顶点的类型集合A有4种类型的取值：class，property，alias，context，分别表示在模式网络中的1个顶点是分类、属性、别名和上下文.关系的类型集合R有3个类型的取值：hypernymy，hyponymy，meronymy，分别表示上位关系、下位关系和整体-部分关系.特别地，给定关联2个顶点u和v的一条边e，如果e被标记为hypernymy，则表示u比v包含的范围更广，即u是v的父节点；如果e被标记为hyponymy，则表示u是v的孩子节点，注意，这2个关系类型hypernymy和hyponymy被更多用来描述2个分类顶点的关系，而关系类型meronymy被更多用来描述分类顶点与属性、别名以及上下文之间的关系.注意的是，分类体系T是1个无环的分类体系.

基于T的定义，根据顶点类型函数θ:VT→A和关系类型函数ψ:ET→R，我们能够获得分类的复合结构.假设C=(c1,c2,…,cm)表示T中分类顶点集合，它用来组织和标注演化知识网络的所有知识项.每个分类c∈C可以表示为微观结构信息：名称name、别名A、上下文描述X、属性P以及它的宏观结构信息：关联的分类集合Nc(表示T中与c关联的所有分类).因此，c可以被表示成1个通过组合微观结构和宏观结构信息的五元组，也被称为c的复合结构：

c=(name,A,X,P,Nc)，

其中，每个属性p∈P通过1个二元组表示：p=(name,aliases)，其中name是属性的名称，aliases是表示属性p的别名集合.

我们注意到，在1个分类体系中，分类集合C是全局的，这意味着一些分类可能在不同分类体系中是一致的.不仅如此，2个分类c和c′之间除了可能存在等价关系之外，c和c′的关系还可能是包含关系，例如c⊆c′或者c′⊆c.由于包含关系可以通过分类之间的等价关系推演出来，因此，本文的目标是判定一个分类体系的分类c是否等价于另一个分类体系的分类c′.由于分类集合C是1个分类体系的全局参数，本文我们只考虑2个分类体系中一对一的分类匹配.下面给出分类体系匹配问题的形式化定义.

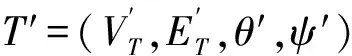
基于定义1，重点介绍基于复合结构的分类体系匹配方法,其具体处理流程如图1所示：

Fig. 1 Pipeline model of composite structure based taxonomy matching method图1 基于复合结构的分类体系匹配方法的管道模型

基于复合结构的分类体系匹配方法主要分为3个步骤：

1) 将每个分类体系T=(VT,ET,θ,ψ)，根据顶点类型函数θ:VT→A和关系类型函数ψ:ET→R转化为以分类为中心的结构表示，这样做的目的是将异构的分类体系转化为相同的结构表示，以此清晰地表达分类体系中分类之间的关系结构.

图2展示了来源于OntoFarm项目*http:nb.vse.cz～svatekontofarm.html构建的2个学术会议本体的部分分类体系.

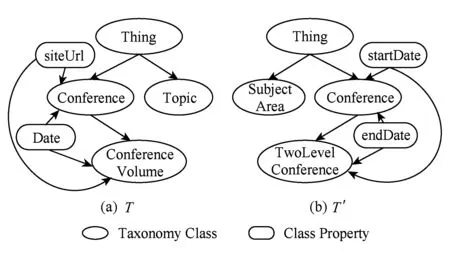
Fig. 2 Two simple taxonomies图2 2个简单的分类体系

基于顶点类型函数θ:VT→A和关系类型函数ψ:ET→R对图2所示的分类体系进行结构转换，转换之后的以分类为中心的结构表示如图3所示：

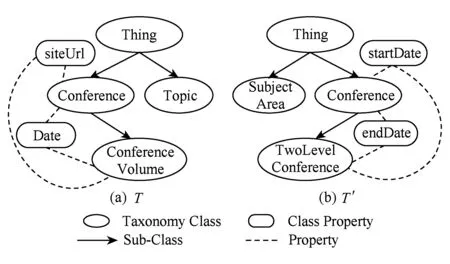
Fig. 3 Class-centered taxonomies图3 以分类为中心的分类体系

2) 基于转换的以分类为中心的分类体系结构，构建二部图模型，建模2个分类体系之间候选的匹配类对之间的关系.

3) 基于步骤2创建的二部图模型，执行最大权匹配剪枝选择2个分类体系之间可能的候选匹配类对，产生分类体系最终的类对匹配结果.

下面介绍基于复合结构的匹配方法BiMWM的原理.

3 BiMWM方法

BiMWM方法将分类体系匹配问题建模为优化问题，即二部图最大权匹配问题进行求解，该方法主要包含2个部分：二部图模型构建算法、分类最大权匹配算法.

3.1 二部图模型构建算法

给定2个分类体系：T=(VT,ET,θ,ψ)和T′=(VT′,ET′,θ,ψ)，为了以统一的方式表示分类所有可用的信息，我们需要一种能够对分类体系T的所有分类C和分类体系T′的所有分类C′之间的所有复杂的关系进行有效编码的表示方式.为了实现这个目标，我们选择二部图作为表示方式，这是因为二部图能够把来自不同分类体系的分类编码成图上的1个顶点，并且可以明确表示顶点之间的候选匹配关系.

在本节，我们基于修改后的以分类为中心的分类体系结构，计算分类的复合结构并构造二部图G=(V,E,W)，以此建模分类体系T和T′之间候选匹配的类对之间的关系.G是1个无向加权图，其中，V是由T中包含的|C|个分类和T′中包含的|C′|个分类组成的顶点集合；E是C和C′之间所有候选匹配类对之间边的集合；W:E→(是实数)是对E中每条边进行权重赋值的函数.

具体来讲，图G=(V,E,W)的构造方式如下：首先，对于分类体系T中的每个分类c∈C，建立其与分类体系T′中可能与其匹配的分类c′∈C′之间的映射(c,c′,w)，其中权重w是基于分类的复合结构信息计算；然后，对每个三元组(c,c′,w)，将c和c′添加到G的顶点集合V中并且将边(c,c′)添加到E中，设置权值函数W(c,c′)=w.

给定1个分类对c和c′，我们基于Sigmoid函数定义它们之间匹配度的权值函数：

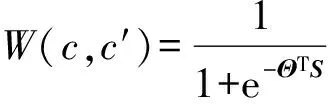
(1)

其中，S=(str(c,c′),prop(c,c′),sem(c,c′),struct(c,c′))T是分类c和c′之间不同结构信息的相似度向量：str(c,c′)，prop(c,c′)和sem(c,c′)是c和c′之间的微观结构的相似度，struct(c,c′)是c和c′之间的宏观结构的相似度.具体地，str(c,c′)表示分类c和c′的名称或别名的相似度；prop(c,c′)表示分类c和c′的属性的相似度；sem(c,c′)表示分类c和c′的语义相似度，而struct(c,c′)则表示分类c和c′之间周围邻居的相似度.Θ=(θ1,θ2,θ3,θ4)T是一个参数向量，用于在进行分类匹配时平衡分类对之间的微观结构信息和宏观结构信息的重要度.

下面将详细介绍2个分类之间微观和宏观结构的相似度度量方法.

1) 微观结构相似度

① 字符串相似度.为了度量字符串之间的相似度，我们基于编辑距离来计算2个分类体系分类之间的相似度.给定2个分类c1和c2，我们定义它们之间的字符串相似度为

其中，Bi={ci.name}∪ci.A是分类ci的名称和别名的集合(i={1,2})；ed(b,b′)是字符串b和b′之间的编辑距离；|·|是字符串的长度.

② 属性相似度.对于属性相似度度量，我们主要基于2个分类包含的相同属性的个数.值得注意的是，分类的某些属性可能比其他属性更具有典型性(typicality),如“人口”一般是国家或地区的属性.为此，我们借鉴信息检索中的逆文档频率的定义，采用如下方式来度量属性p的典型度：

其中，tp表示分类属性p的典型度，#(·)表示数量.基于属性的典型度，我们采用加权的Jaccard相似系数来定义2个分类之间的属性相似度：

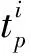
③ 语义相似度.在语义相似度方面，目前已经有很多工作，例如Resnik[22]和Banerjee等人[23]提出的基于WordNet计算不同字符串之间的语义相关性的方法，本文直接采用Banerjee提出的Lesk算法[23]来计算2个分类之间的语义相似度.给定分类c1和c2，本文把它们之间的语义相似度定义为

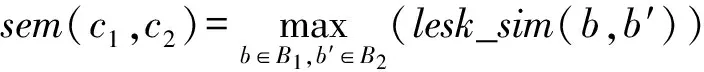
其中，如字符串相似度中所述，Bi是分类ci的名称和别名组成的集合(i={1,2});lesk_sim(b,b′)是基于Lesk算法的语义相似度.

2) 宏观结构相似度

① 近邻相似度.近邻相似度通过利用分类的邻居信息来度量2个分类的相似度.对于近邻相似度计算，我们主要基于2个分类周围公共邻居分类的个数.因此，我们直接使用Jaccard相似系数来定义分类c1和c2之间的近邻相似度：

其中，ci.Nc是分类ci的邻居分类的集合(i={1,2})，|·|表示集合的大小.

基于上述分类之间相似度计算方式的定义，给定分类体系T=(VT,ET,θ,ψ)和T′=(VT′,ET′,θ,ψ)，为了构造表示这2个分类体系中分类匹配关系的二部图模型，我们首先将T中包含的所有分类作为二部图的左部顶点，T′中包含的分类作为二部图的右部顶点，然后在这些顶点之间利用式(1)计算左部顶点与右部顶点之间匹配的可能性；接下来为左部顶点和右部顶点之间分配连边信息并为连边分配权重，从而生成T和T′之间的无向加权二部图G=(V,E,W).其中，在二部图G=(V,E,W)构造过程中，V，E，W被初始化为空集.二部图构造算法如算法1所示：

算法1. 二部图构造算法.

输入：T=(VT,ET,θ,ψ)，T′=(VT′,ET′,θ,ψ)；

输出：二部图G=(V,E,W).

① 初始化G=(V,E,W)：V=∅,E=∅,W=∅；

② FOR ALLc∈VTinTDO

③ FOR ALLc′∈VT′inT′ DO

④ 基于分类的复合结构信息利用式(1)计算分类c和c′等价匹配的可能性w；

⑤ IFw>0 THEN

⑥ 将分类c和c′添加到顶点集合V中；

⑦ 将权值函数W(c,c′)=w添加到W中；

⑧ 将边e=(c,c′)添加到边集合E中；

⑨ 为边e=(c,c′)赋权值w；

⑩ END IF

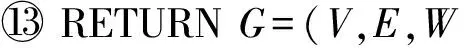
具体地，算法1主要包含2个步骤：

1) 候选匹配分类选取.在这一步中，对来自分类体系T的每一个分类c，我们把它和T′的每个分类c′进行配对，根据式(1)计算c和c′之间的匹配度w=W(c,c′)，从T′选择所有可能与c匹配的分类c′(行②～⑥).

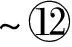
利用上述二部图模型构建方法，对图3中的2个分类体系构造二部图，以此建模2个分类体系之间候选匹配的类对之间的关系.对这2个分类体系构造的二部图模型如图4所示：

Fig. 4 An example of the bipartite graph between two taxonomies图4 二部图模型示例

在图4中，该二部图由T中分类组成的二部图的左部顶点和T′中分类组成的右部顶点，以及这些顶点之间可能的候选连边组成.

3.2 分类最大权匹配算法

在本节，我们将给出在二部图上通过最大权匹配算法找到2个分类体系最优等价映射的过程.下面，我们首先介绍如何将分类体系匹配问题形式化表示为二部图上的最大权匹配问题，然后给出求解该问题的最大权匹配算法.

如上所述，分类体系匹配问题是一个最优化问题，其目标是找到具有最高置信度的最优等价分类之间一对一的映射；而最大权匹配的目标是找到一组权值最大的顶点不相交的边集合，而该集合与分类体系之间的最优匹配M是等价的.因此，很容易将分类体系匹配问题转换成最大权匹配问题.

具体来说，给定1个二部图G=(V,E,W)，分类体系匹配问题可以被建模成图G上的整数线性规划问题，问题的形式化定义如式(2)所示：

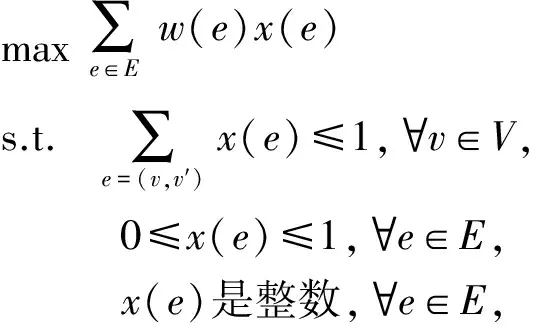
(2)

其中，x表示顶点之间是否匹配，w表示顶点之间匹配的可能性.

该整数线性规划问题可以转化为其对偶问题进行求解：顶点覆盖问题，即在图G=(V,E,W)中找出具有最小规模的顶点覆盖V′⊆V，满足如果(v,v′)∈E，则v∈V′或v′∈V′.这个对偶问题已被证明是一个NP完全问题，问题定义如式(3)所示：

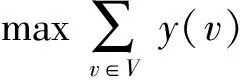
s.t. y(e)≥w(e),∀e∈E,

(3)

y(v)≥0,∀v∈V，

获得最大权匹配的核心思想是在二部图中通过1个初始匹配，不断地查找增广路径，直到找不到增广路径为止.最经典的求解最大权匹配的算法是匈牙利算法[24].由于我们构建的二部图的权值是实数，因此我们扩展匈牙利算法，给出针对分类体系匹配问题的二部图最大权匹配算法，下面详细介绍该算法.

给定一个二部图G=(V,E,W)，我们使用M表示具有最大权的顶点不相交的边集合，初始时M被初始化为空集；VL和VR分别表示G中左部顶点集合和右部顶点集合；LF和RF分别表示G中左边自由的顶点集合和右边自由的顶点集合(当前还未被选择放入M的顶点的集合)，初始时LF=VL，RF=VR；y(v)表示顶点v∈V的对偶变量值；δ表示对偶变量的增广值，初始数值为δ0=max{W(e)|e∈E}.

最大权匹配算法的执行流程如算法2所示：

算法2. 最大权匹配算法BiMWM.

输入：G=(V,E,W)，M，VL，VR，LF，RF，δ0;

输出：最大权匹配M={(v,v′)|v∈VL,v′∈VR}.

① FOR ALLv∈VinGDO

② IFv∈VLTHEN

③y(v)=δ0；

④ ELSE

⑤y(v)=0；

⑥ END IF

⑦ END FOR

⑧ REPEAT

⑨ 根据VL,VR,LF,RF利用算法3查找增广路径AP；

⑩ 扩展匹配M:M=M⊕AP；

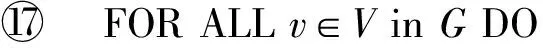
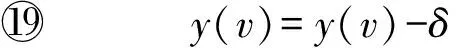
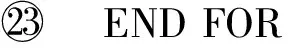
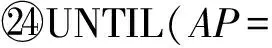
具体地，BiMWM算法主要包含4个步骤：

1) 初始化对偶变量.使用对偶变量增广值δ的初始值δ0初始化对偶变量y(v)(行①～⑦).

2) 查找增广路径并根据增广路径修改当前找到的最大权匹配.执行算法3查找一条增广路径(行⑨)，基于增广路径修正最大权匹配结果(行⑩).

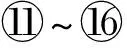
重复执行步骤2～4，直至G中找不到增广路径，算法终止.至此，我们获得二部图G=(V,E,W)上的最大权匹配M.

在BiMWM算法中，增广路径查找流程如下：

1) 修改二部图G，将其转换为有向图以便查找增广路径.具体修改方式如下：

① 为图G中的边添加方向：在G中每一个左部未匹配的顶点LF和右部未匹配的顶点RF之间添加LF→RF方向的连边；对最大权匹配M中属于右部的匹配顶点MR=VRRF和属于左部的匹配顶点ML=VLLF之间添加MR→ML的连边.

② 在修改的有向图上添加源顶点s和汇聚顶点t，并在顶点s和每一个属于左部的自由顶点vL∈LF之间添加s→vL方向的连边；在每一个属于右部的自由顶点vR∈RF和汇聚顶点t之间添加vR→t方向的连边.

基于上述方式，即可将二部图G转换为1个有向图.图5展示了根据匹配结果将图4中所示的二部图G=(V,E,W)转换为有向图之后的1个结果.

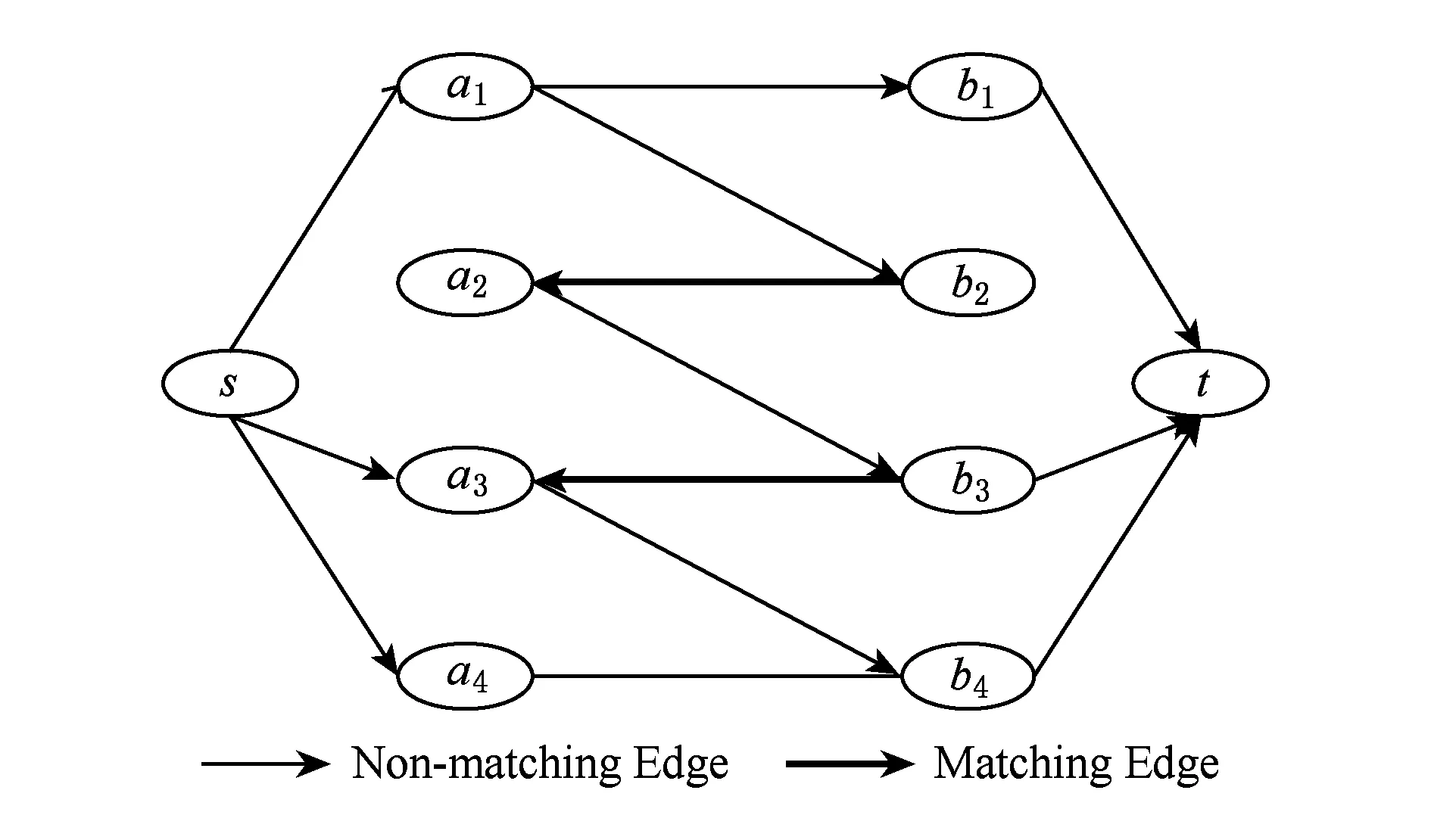
Fig. 5 Extended bipartite graph图5 扩展的二部图模型

2) 在修改之后的有向图上执行广度优先算法(breadth first search, BFS)，便可遍历图中所有顶点，得到1个顶点访问的序列，从而找到由该顶点序列组成的1条增广路径.

增广路径查找算法的执行流程如算法3所示：

算法3. 增广路径查找算法.

输入：G=(V,E,W)，M，{y(v)|v∈V}，VL，VR，LF，RF；

输出：增广路径AP.

① IFLF=∅ ORRF=∅ THEN

②AP=∅；

③ ELSE

④ 在未匹配的顶点对之间添加从VL→VR的有向边，在匹配的顶点对之间添加从VR→VL的有向边；

⑤ 添加源顶点s和汇聚顶点t，并分别在它们与每一个左部自由顶点vL∈LF和右部自由顶点vR∈RF之间添加有向边：s→vL,vR→t；

⑥ 在修改的图G上执行BFS算法查找增广路径AP={(v,v′)|v∈LF,v′∈RF}，其中AP中所有的边满足以下约束条件：y(v)+y(v′)=W(v,v′)；

⑦ END IF

⑧ 根据增广路径AP更新自由顶点集合LF=LFAP，RF=RFAP；

⑨AP=AP{s,t}；

⑩ RETURNAP.

算法复杂度分析：给定2个分类体系T=(VT,ET,θ,ψ)和T′=(VT′,ET′,θ,ψ)，记T中包含的分类的个数为n，T′中包含的分类个数为n′.如算法1所示，我们的方法需要n×n′步计算T和T′中所有分类对之间匹配的可能性.因此，我们的方法将会花费O(nn′)的时间创建二部图G=(V,E,W).

设m=|E|表示图G中边的个数，根据算法3，基于图的广度优先搜索我们可以在O(m)时间内找到1条增广路径.设l=min{n,n′}表示2个分类体系至多可能匹配的分类对个数，如算法2所示，BiMWM则需要花费O(lm)的时间来完成图G中最大权匹配的查找.因此，我们的方法可以在多项式时间内O(nn′+lm)获得2个分类体系匹配的类对，找到2个分类体系包含的语义相同的公共分类.

众所周知，二部图最大权匹配的目标是在二部图中查找一组顶点不相交的边，使得这组边的权值和最大.所以，最大权匹配的解决方案是一个全局最优的顶点不相交的边集.在本文中，我们提出将分类体系匹配问题建模成最大权匹配问题.因此，对于2个分类体系，我们的方法可以保证获得一个全局的具有最高置信度的最优匹配.

4 实验与分析

在本节中，我们在2个标准数据集上评估我们提出的基于复合结构的知识库分类体系匹配方法BiMWM的效果.我们将：1)在准确率、召回率和F值3个指标上比较BiMWM方法和基准方法的效果；2)分析BiMWM方法在分类体系规模变化时的性能变化；3)分析BiMWM方法在不同领域分类体系上的有效性.本节所有实验是在2台配置相同的服务器上完成的，服务器具体配置如下：64-bit Linux OS，16 core 2 GHz AMD OpteronTM6128处理器，32 GB RAM.

4.1 实验设置

1) 评价指标.在实验中我们使用标准的评价指标：准确率、召回率和F值，度量分类体系中正确匹配的类对的数目.除此之外，我们使用运行时间度量各个方法在不同规模数据集上的运行效率.

2) 数据集.在实验中使用本体映射任务国际评测①(ontology alignment evaluation initiative, OAEI)中发布的2个标准数据集.

第1个数据集来自于OAEI 2013的生物医学领域的测试用例②(记为largebio)，该测试用例包含3个生物医学本体：FMA，SNOMED-CT(以下简记为SNOMED)，NCI，这些本体都包含数万的分类.该测试用例的主要目标是寻找这些本体之间的分类匹配映射.由于该测试用例包含3个不同的本体，因此分成不同的匹配问题：FMA-NCI，FMA-SNOMED，NCI-SNOMED，而每一个匹配问题又被分成了“局部”和“整体”片段上的2个测试任务，分别记为DSsmall和DSwhole数据集，以便评测不同方法在不同规模数据集上的性能表现.该测试用例使用一体化医学语言系统UMLS词表作为本体匹配的标注数据(ground truth)，该数据集分类的规模约为27万.

第2个数据集来自OAEI 2013的学术会议领域的测试用例③(记为DSconf)，其目标是要找到学术会议领域的本体集合中所有正确的匹配关系.在该测试用例中，我们采用标记ra1的数据集作为ground truth，其包括7个本体，即21个本体匹配映射问题，这些本体来源于OntoFarm项目④.

3) 基准方法.为了验证BiMWM方法在分类匹配任务上的有效性，在实验中我们选择OAEI 2013评测中[8]在各项评价指标上效果排名靠前的4种方法作为基准方法，它们分别是YAM++，IAMA，LogMap，ServOMap.除此之外，我们还选择基于贪心的方法SiGMa[6]作为基准方法(见第1节).

4) 参数设置.在实验中，测量2个分类之间的匹配可能性的权值函数的参数Θ=(θ1,θ2,θ3,θ4)T被设置为Θ=(0.39,0.41,0.10,0.10)T，该参数是我们通过探讨BiMWM方法在会议数据集上的有效性找到的合理值.在所有数据集上，我们都固定这些参数进行效果比对.另外，由于SiGMa开始于1个初始的匹配分类对，该分类对可以是任意具有高质量的初始匹配种子[6].由于选用的OAEI标准数据集中所有分类体系的根节点都是名为“Thing”的分类，因此，在实验中我们选择标准数据集的根节点之间组成的类对作为SiGMa初始匹配的分类对.

基于上述实验设置，我们进行：①测试各个方法在不同规模数据集上的运行效果;②进一步测试各个方法在不同领域数据集上的有效性;③对实验结果进行分析.

4.2 实验结果

1) 不同规模数据集的测试结果

为了测试BiMWM和基准方法在不同规模数据集上分类匹配的有效性，在本节我们分别在DSsmall和DSwhole数据集上对这些方法进行了测试.

表1和表2分别展示了针对OAEI 2013生物医学领域测试用例中所有的匹配问题(FMA-NCI，FMA-SNOMED，NCI-SNOMED)上，这些方法在DSsmall和DSwhole数据集上的分类匹配的准确率、召回率和F值以及这些方法的运行时间.在表1和表2中，对于每一项评价指标，效果最好的用粗体表示.

从表1和表2可以看出，不管是在DSsmall数据集还是在DSwhole数据集，BiMWM在所有匹配问题上都能获得相对更高的准确率、召回率和F值；在运行效率方面，虽然在DSsmall和DSwhole数据集中所有匹配问题上BiMWM没有SiGMa运行效率高，但是除了在DSsmall数据集中的FMA-SNOMED和NCI-SNOMED匹配问题上BiMWM运行效率次于IAMA外，在剩余的匹配问题上BiMWM的运行效率都优于基准方法.

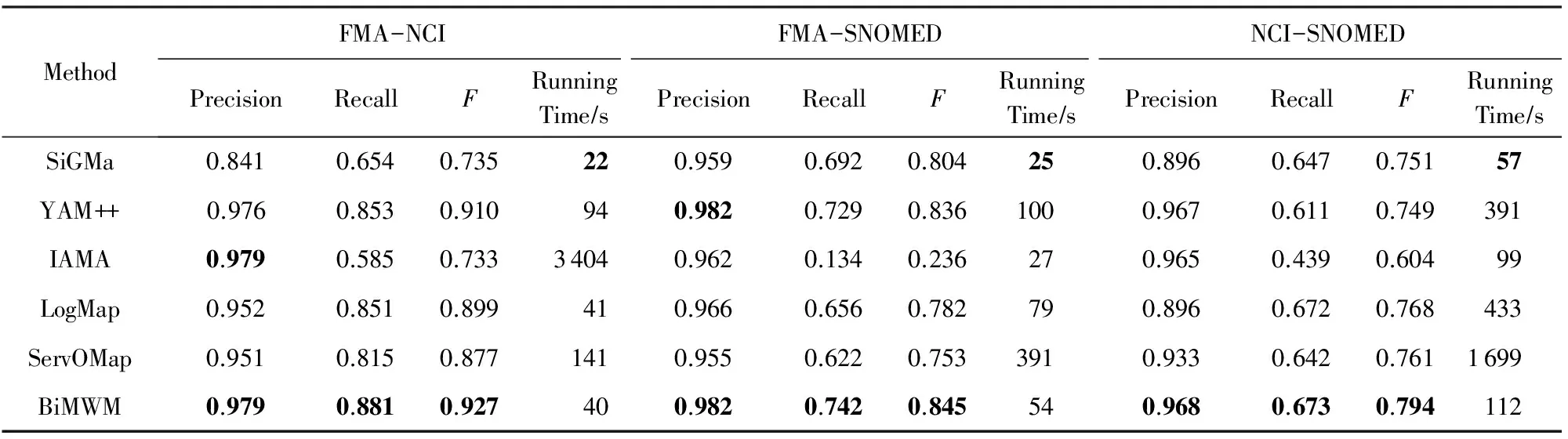
Table 1 Comparison over the DSsmall Dataset

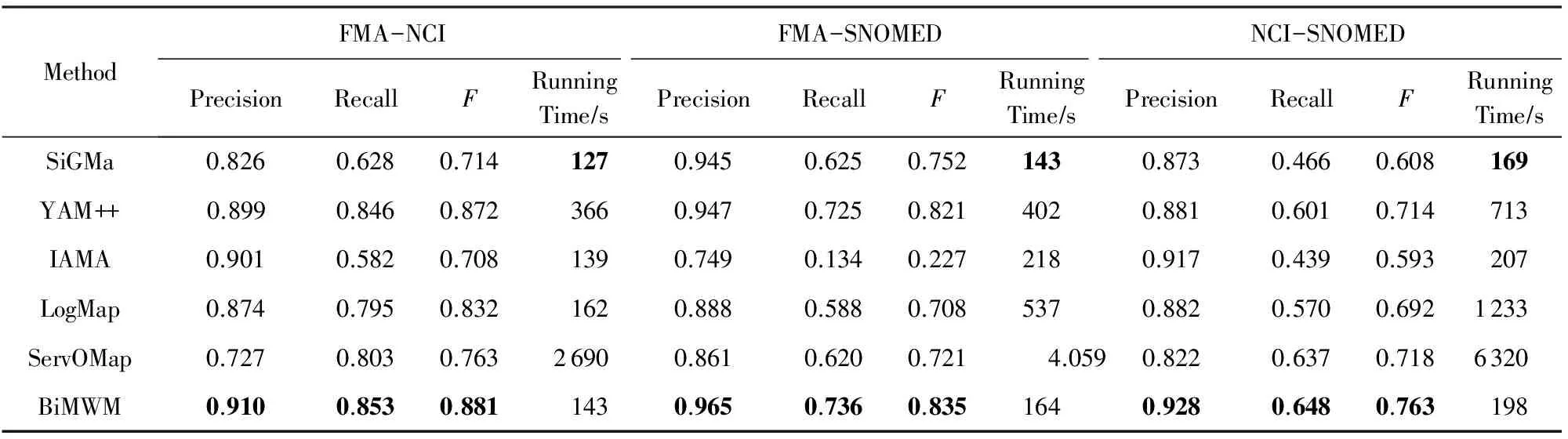
Table 2 Comparison over the DSwhole Dataset

BiMWM和基准方法在DSsmall和DSwhole数据集上整体的实验结果如表3所示.从表3中可以发现与基准方法相比，BiMWM在所有规模的largebio数据集上都能获得最好的准确率、召回率和F值.而且，与表现最好的YAM++方法相比，BiMWM方法分类匹配的F值在DSsmall和DSwhole数据集上分别有2.3%和3.3%的提高.不仅如此，在运行效率上，BiMWM花费的时间仅是YAM++花费时间的13，运行效率提升近2倍.尽管BiMWM的运行时间比基于贪心策略的SiGMa方法稍高，但是我们可以看到，BiMWM在DSsmall和DSwhole的largebio数据集上都获得了超过83%的F值，大大超过基准方法SiGMa.

除此之外，从表3中我们可以发现，所有方法在“局部”测试集上的效果好于在“整体”测试集上的效果.导致这一现象最可能的原因是对于分类体系中的每一个分类来说，与较大的分类体系中的分类进行匹配时会产生更多可能的候选选择，在这种情况下更难以在保证召回率的前提下保证较高的准确率，反之亦然.尽管如此，无论在“局部”数据集还是在“整体”数据集上，BiMWM都保持最好的准确率、召回率和F值，并且BiMWM表现相对稳定，这也证明了BiMWM方法可以很好地适应不同规模的分类体系匹配.

Table 3 Average Comparison over the DSsmall and DSwhole Datasets

2) 不同领域数据集的测试结果

在本节中，我们将评估BiMWM方法和基准方法在largebio和会议数据集上的分类体系匹配的性能.

为了比较所有方法在largebio数据集上的综合效果，我们对这些方法在largebio数据集“局部”和“整体”片段上的结果求平均，实验结果如表4所示：

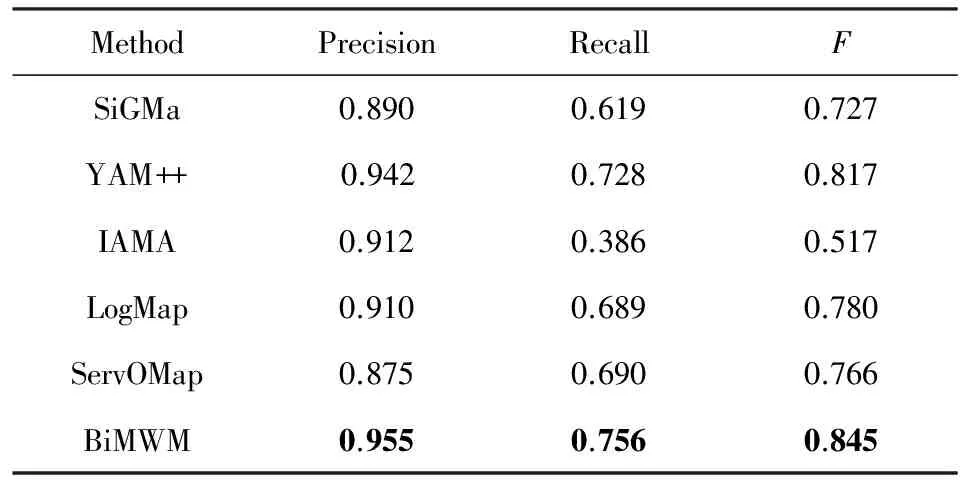
Table 4 Comparison over the largebio Datasets

从表4中，我们可以发现BiMWM的准确率比基准方法表现最差的ServOMap提高了8%，比基准方法表现最好的YAM++提高了1.3%;同时，BiMWM的召回率比基准方法表现最差的IAMA提高了37%，比基准方法表现最好的YAM++提高了2.8%;在综合指标F值上，BiMWM比基准方法表现最差的IAMA提高了32.8%，比基准方法表现最好的YAM++提高了2.8%.总的来说，与基准方法相比，BiMWM在largebio数据集上分类匹配的准确率、召回率和F值都最好.因此，该实验表明BiMWM能够在largebio数据集上比基准方法具有更好的性能.

下面，我们测试这些方法在会议数据集DSconf上的效果.由于DSconf数据集包含7个不同的本体，因此我们把这些本体组成的21个本体匹配映射任务的结果作为整体来评价这些方法的效果.在DSconf数据集上的实验结果如表5所示：

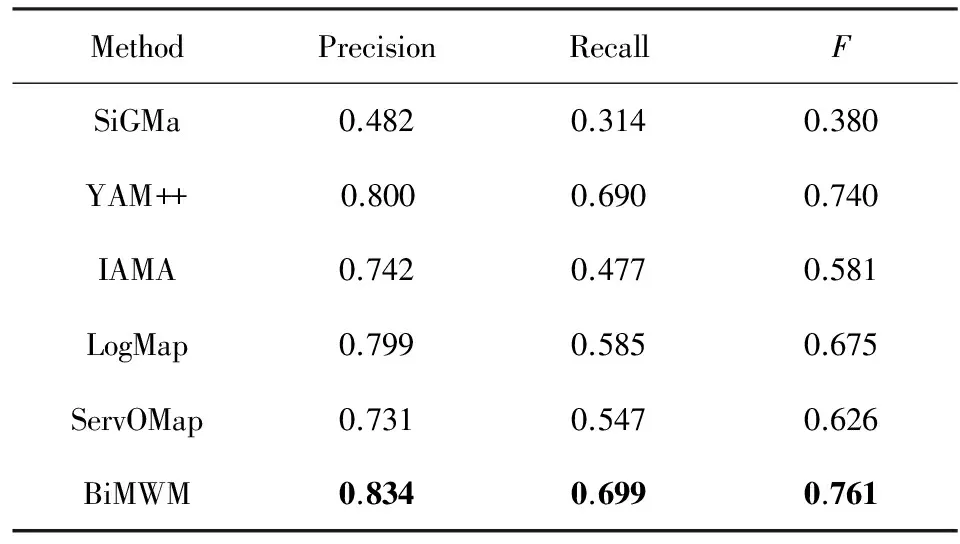
Table 5 Comparison over the DSconf Dataset

从表5中可以看出，BiMWM的准确率比基准方法表现最差的SiGMa提高了35.2%，比基准方法表现最好的YAM++提高了3.4%；同时，BiMWM的召回率比基准方法表现最差的SiGMa提高了38.5%，比基准方法表现最好的YAM++提高了0.9%；BiMWM的F值比基准方法表现最差的SiGMa提高了38.1%，比基准方法表现最好的YAM++提高了2.1%.因此，与基准方法相比，该实验表明BiMWM在DSconf数据集上具有更好的效果.

为了清晰地描述BiMWM和基准方法在不同领域分类体系下的性能变化，图6展示了这些方法在largebio数据集和会议数据集上的实验结果.

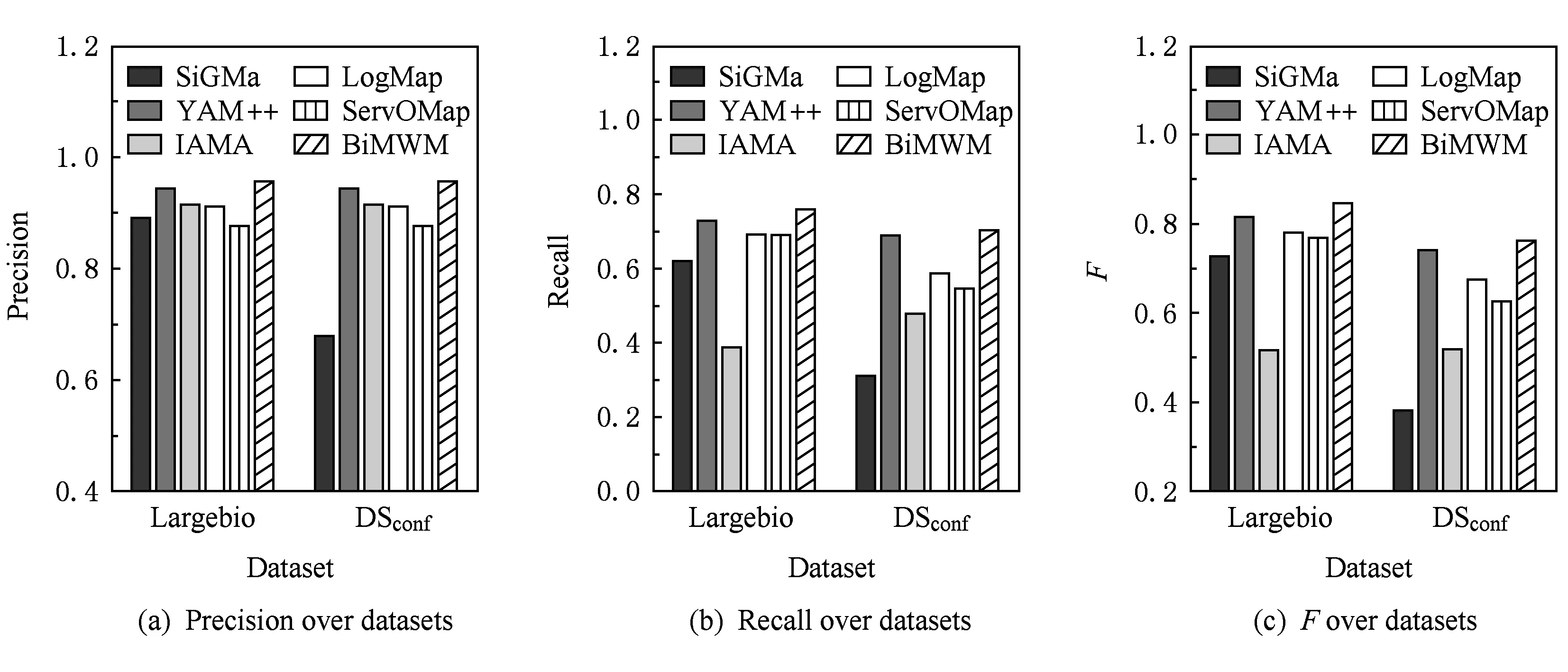
Fig. 6 Comparison over the datasets from different domains图6 不同领域数据集上方法性能的变化

从图6中可以看出，所有方法中除BiMWM和YAM++外，其他方法在largebio数据集和DSconf会议数据集上的性能波动比较大.虽然BiMWM和YAM++在这2个数据集上性能相对稳定，但是与YAM++相比，BiMWM在这2个数据集上都获得了最好的准确率、召回率和F值.该实验证明了BiMWM方法可以在不同领域的分类体系上很好地完成分类匹配任务.

基于以上实验分析可以看出，与基准方法相比，BiMWM不仅可以在不同规模的分类体系上获得更好的效果，而且在不同领域的分类体系上也能获得更好的效果，这些都表明BiMWM方法的有效性，这也说明在分类体系匹配过程中采用分类的复合结构是非常有用的技术，这表明了不管分类体系的规模和所属领域，它们在结构上具有很多共同点.

5 总 结

针对当前单一的分类体系匹配方法不适应异构、大规模的分类体系匹配的扩展性问题，本文从分类的结构特征出发，提出了一种基于复合结构的知识库分类体系匹配方法BiMWM.该方法借助分类体系结构上的共同点，基于分类的微观结构和宏观结构特征，将分类体系匹配问题转化为二部图上的优化问题，同时利用二部图模型建模2个分类体系之间候选匹配的类对之间的关系，最后通过执行最大权匹配算法剪枝选择2个分类体系之间可能的候选匹配类对，产生2个分类体系之间的全局最优匹配.实验结果证明该方法能够有效支持大规模分类体系匹配，不仅如此，该方法在不同的分类领域和不同规模的分类体系中都表现出很好的适应性.

[1]Bollacker K, Evans C, Paritosh P, et al. Freebase: A collaboratively created graph database for structuring human knowledge[C]Proc of 2008 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2008: 1247-1250

[2]Fabian M S, Gjergji K, Gerhard W. YAGO: A core of semantic knowledge unifying WordNet and wikipedia[C]Proc of the 16th Int World Wide Web Conf. New York: ACM, 2007: 697-706

[3]Wu Wentao, Li Hongsong, Wang Haixun, et al. Probase: A probabilistic taxonomy for text understanding[C]Proc of 2012 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2012: 481-492

[4]Li Juanzi, Tang Jie, Li Yi, et al. RiMOM: A dynamic multistrategy ontology alignment framework[J]. IEEE Trans on Knowledge and Data Engineering, 2009, 21(8): 1218-1232

[5]Suchanek F M, Abiteboul S, Senellart P. PARIS: Probabilistic alignment of relations, instances, and schema[J]. The VLDB Endowment, 2011, 5(3): 157-168

[6]Lacoste-Julien S, Palla K, Davies A, et al. SiGMa: Simple greedy matching for aligning large knowledge bases[C]Proc of 2013 ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2013: 572-580

[7]Demidova E, Oelze I, Nejdl W. Aligning freebase with the YAGO ontology[C]Proc of the 22nd ACM Int Conf on Information and Knowledge Management. New York: ACM, 2013: 579-588

[8]Grau B C, Dragisic Z, Eckert K, et al. Results of the ontology alignment evaluation initiative 2013[C]Proc of the 8th ISWC Workshop on Ontology Matching. New York: ACM, 2013: 61-100

[9]Wang Yuanzhuo, Jia Yantao, Liu Dawei, et al. Open Web knowledge aided information search and data mining[J]. Journal of Computer Research and Development, 2015, 52(2): 456-474 (in Chinese)(王元卓, 贾岩涛, 刘大伟, 等. 基于开放网络知识的信息检索与数据挖掘[J]. 计算机研究与发展, 2015, 52(2): 456-474)

[10]Lin Hailun, Jia Yantao, Wang Yuanzhuo, et al. Populating knowledge base with collective entity mentions: A graph-based approach[C]Proc of IEEEACM Int Conf on Advances in Social Networks Analysis and Mining. Piscataway, NJ: IEEE, 2014: 604-611

[11]Zhuang Yan, Li Guoliang, Feng Jianhua. A survey on entity alignment of knowledge base[J]. Journal of Computer Research and Development, 2016, 53(1): 165-192 (in Chinese)(庄严, 李国良, 冯建华. 知识库实体对齐技术综述[J]. 计算机研究与发展, 2016, 53(1): 165-192)

[12]Shvaiko P, Euzenat J. A survey of schema-based matching approaches[J]. Journal on Data Semantics, 2005, 5: 146-171

[13]Kumar S, Singh V. Multi-strategy based matching technique for ontology integration[J]. Computational Intelligence in Data Mining, 2015, 3: 135-148

[14]Shvaiko P, Euzenat J. Ontology matching: State of the art and future challenges[J]. IEEE Trans on Knowledge and Data Engineering, 2013, 25(1): 158-176

[15]Vargas-Vera M, Nagy M. State of the art on ontology alignment[J]. International Journal of Knowledge Society Research, 2015, 6(1): 17-42

[16]Chen R C, Bau C T, Yeh C J. Merging domain ontologies based on the wordnet system and fuzzy formal concept analysis techniques[J]. Applied Soft Computing, 2011, 11(2): 1908-1923

[17]Ba M, Diallo G. Large-scale biomedical ontology matching with ServOMap[J]. IRBM, 2013, 34(1): 56-59

[18]Jiménez-Ruiz E, Grau B C. Logmap: Logic-based and scalable ontology matching[C]Proc of Int Conf on Semantic Web. Berlin: Springer, 2011: 273-288

[19]Li Chunhua, Cui Zhiming, Zhao Pengpeng, et al. Improving ontology matching with propagation strategy and user feedback[C]Proc of the 7th Int Conf on Digital Image Processing. Los Angeles: ISOP, 2015: 963127

[20]Gruber T R. A translation approach to portable ontology specifications[J]. Knowledge Acquisition, 1993, 5(2): 199-220

[21]Jia Yantao, Wang Yuanzhuo, Cheng Xueqi, et al. OpenKN: An open knowledge computational engine for network big data[C]Proc of IEEEACM Int Conf on Advances in Social Networks Analysis and Mining. Piscataway, NJ: IEEE, 2014: 657-664

[22]Resnik P. Using information content to evaluate semantic similarity in a taxonomy[C]Proc of the 14th Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 1995: 448-453

[23]Banerjee S, Pedersen T. An adapted Lesk algorithm for word sense disambiguation using WordNet[C]Proc of Computational Linguistics and Intelligent Text Processing. Berlin: Springer, 2002: 136-145

[24]Kuhn H W. The Hungarian method for the assignment problem[J]. Naval Research Logistics Quarterly, 1955, 2(12): 83-97

Lin Hailun, born in 1987. PhD and assistant professor. Her main research interests include open knowledge network, information extraction.

Jia Yantao, born in 1983. PhD and assistant professor. His main research interests include open knowledge network, social computing, combinatorial algorithms.

Wang Yuanzhuo, born in 1978. PhD and associate professor. His main research interests include social computing, open knowledge network, network security analysis, stochastic game model, etc.

Jin Xiaolong, born in 1976. PhD, associate professor and PhD supervisor. His main research interests include social computing, multi agent systems, performance modeling and evaluation, etc.

Cheng Xueqi, born in 1971. PhD, professor and PhD supervisor. His main research interests include network science, Web search, data mining, etc.

Wang Weiping, born in 1975. PhD, professor and PhD supervisor. His main research interests include big data storage and processing.

A Composite Structure Based Method for Knowledge Base Taxonomy Matching

Lin Hailun1, Jia Yantao2, Wang Yuanzhuo2, Jin Xiaolong2, Cheng Xueqi2, and Wang Weiping1

1(InstituteofInformationEngineering,ChineseAcademyofSciences,Beijing100093)2(KeyLaboratoryofNetworkDataScienceandTechnology(InstituteofComputingTechnology,ChineseAcademyofSciences),ChineseAcademyofSciences,Beijing100190)

Taxonomy matching, i.e., an operation of taxonomy merging across different knowledge bases, which aims to align common elements between taxonomies, has been extensively studied in recent years due to its wide applications in knowledge base population and proliferation. However, with the continuous development of network big data, taxonomies are becoming larger and more complex, and covering different domains. Therefore, to pose an effective and general matching strategy covering cross-domain or large-scale taxonomies is still a considerable challenge. In this paper, we presents a composite structure based matching method, named BiMWM, which exploits the composite structure information of class in taxonomy, including not only the micro-structure but also the macro-structure. BiMWM models the taxonomy matching problem as an optimization problem on a bipartite graph. It works in two stages: it firstly creates a weighted bipartite graph to model the candidate matched classes pairs between two taxonomies, then performs a maximum weight matching algorithm to generate an optimal matching for two taxonomies in a global manner. BiMWM runs in polynomial time to generate an optimal matching for two taxonomies. Experimental results show that our method outperforms the state-of-the-art baseline methods, and performs good adaptability in different domains and scales of taxonomies.

knowledge base; taxonomy matching; composite structure; bipartite graph; maximum weight matching

2015-09-22；

2016-05-16

国家“九七三”重点基础研究发展计划基金项目(2012CB316303,2013CB329602)；“核高基”国家科技重大专项(2013ZX01039-002-001-001)；国家自然科学基金项目(61303056,61402464,61402442,61572469,61502478)；北京市自然科学基金项目(4154086) This work was supported by the National Basic Research Program of China (973 Program) (2012CB316303, 2013CB329602), the National Science and Technology Major Projects of Hegaoji (2013ZX01039-002-001-001), the National Natural Science Foundation of China (61303056, 61402464, 61402442, 61572469, 61502478), and the Beijing Natural Science Foundation (4154086).

王伟平(wangweiping@iie.ac.cn)

TP391

��机研究与发展

10.7544issn1000-1239.2017.20150796 Journal of Computer Research and Development54(1): 63-70， 2017