事件触发关键级提升的实时任务可调度性分析

黄丽达 李仁发

(湖南大学信息科学与工程学院 长沙 410082)(hld_jt@hnu.edu.cn)

事件触发关键级提升的实时任务可调度性分析

黄丽达 李仁发

(湖南大学信息科学与工程学院 长沙 410082)(hld_jt@hnu.edu.cn)

混合关键级(mixed criticality, MC)系统能够同时保证高效地资源利用与高关键任务的正确执行.当前，对混合关键级系统的研究多认为，从低关键级提升到高关键级的时机是高关键级任务执行超过其低关键级模式下时间预算的时刻.但在实际应用的嵌入式系统中，关键级模式的提升是由诸如所处环境变化、控制切换等系统外部事件触发的，即关键级的提升可能发生在任务执行过程中的任何时刻.在单处理器平台上，针对使用固定优先级调度策略的周期任务集，当外部事件触发关键级提升后，基于响应时间分析得出了可调度高关键级任务的必要条件；并对关键级提升后，高关键级任务可能通过优先级交换满足截止时限的条件进行了分析，得出了相应的优先级交换算法.仿真实验验证了事件触发关键级提升时高关键级任务的可调度性及优先级交换算法的有效性.

关键级；事件触发；优先级；响应时间；截止时限

现代实时嵌入式系统，例如航空电子设备以及汽车系统的实际应用，正向着功能不断增加但所占空间更小、重量更轻、成本更低、能耗更少的方向发展.因此使用冗余硬件分层设计来实现任务之间隔离执行[1]的传统方法，正向着不同关键级的多种功能集成到一块物理平台上，共享硬件资源的研究方向转变.但这种以提高资源利用率为目的的共享可能会使低关键级(low criticality, LO)任务对高关键级(high criticality, HI)任务的正确执行产生干扰，导致HI任务错过截止时限、造成非常严重的后果.例如从高效利用处理器计算能力的角度，可以将汽车的防抱死制动任务与导航任务放在同一个处理器上执行，若导航任务未能按预设时间执行完毕，防抱死任务很可能就无法得以及时执行，从而导致重大安全事故[2].

既要确保HI任务的截止时限又要保证充分利用资源，是提出混合关键级(mixed criticality, MC)系统的初衷.文献[3]首先对混合关键级系统的调度与验证进行了讨论.无论是从过载角度考虑以增加系统运行的鲁棒性[4]，还是从静态验证、遵循更保守国际统一标准的角度出发[5]，MC系统的执行可分成若干关键级模式，处于不同关键级模式所确保执行的任务子集和任务属性均不同，即将待调度任务集划分为不同关键级：在高关键级HI模式和关键级LO模式下总是满足HI任务的截止时限；而LO任务只在低关键级模式下执行，不确保其在HI模式下满足截止时限.一般认为系统是从LO模式开始运行，MC系统执行从LO模式切换到HI模式的过程称之为关键级提升.

MC任务一个重要特点是除了截止时限(dead-line)、周期(period)、最差情况下执行时间(worst case execution time, WCET)、释放时间(release time)等传统时间参数之外，还增加了关键级(criticality)这一参数，且部分或全部的时间参数值依赖于关键级，即所谓关键参数：相较于LO模式，HI任务在HI模式下WCET更长、执行频率更高、截止时限更短[6].虽然有以文献[7]为代表的部分研究讨论不同关键级模式下基于弹性模型的周期变化，但当前以文献[8-11]为代表的大多数MC调度研究，包括最早提出MC调度的文献[3]，均是以WCET为关键参数.与周期、截止时限等其他时间参数比较，虽然实时任务的实际执行时间具有不确定性和动态持续性，但是作为实时任务时间参数之一的WCET则是可以通过预先估算获得.典型MC系统对于关键级的提升通常是这样描述的：HI任务在LO模式下执行时，若执行完毕其LO模式下预置的WCET时间预算，仍然没有结束执行，则认为此时系统应该切换到HI模式执行，同时通过挂起或抛弃LO任务以确保HI任务获得更多的处理器执行时间.这是从任务本身执行发生变化的角度来识别关键级模式提升时刻.

但实际上，与系统关键级回落[12]不同，系统关键级模式从低到高的切换并不是由正在执行的任务引发的，而是由外部事件触发的.文献[13]中指出现代汽车系统随着行驶环境的变化发生关键级变化，例如从Street(城市街道)执行模式进入Highway(高速公路)执行模式时，其悬架控制功能从LO切换成HI模式执行.又例如，从权威机构标准认证角度考虑MC系统时，经常以无人机为典型实例，文献[14]中指出当军用无人机飞入民航区域，涉及飞行安全的相关功能必须遵循更保守的时间限制，例如WCET增加等，可见关键级的提升也是由系统所处外部环境变化引起的.因此，系统执行从LO模式提升到HI模式，不是由任务本身触发这种关键级提升，而是由外部环境变化、人为控制等事件的发生才引发系统关键级提升.任务实际执行时间超过低关键级WCET只是关键级提升的表现和需要.

不同于当前以HI任务超出低关键级WCET作为关键级提升时刻的思路，本文基于外部事件触发(event-trigger)系统关键级提升的观点，对关键级提升期间HI任务的可调度性进行分析.由于在不同关键级下需确保执行的任务集在系统设计时就已经确定好了，即可以离线确定系统静态处于某一关键级模式下的调度策略，保证具有相应关键级参数的任务截止时限[15].所以要确保HI任务的正确执行，问题聚焦在从LO提升到HI这个模式动态切换期间如何满足HI任务的截止时限.本文基于响应时间分析，针对在单处理平台上执行的混合关键级实时周期任务集，讨论了其从LO模式切换到HI模式的关键级提升期间的可调度性，得出了相关必要的可调度条件.

在已公开发表的文献中，涉及关键级提升后优先级是否可交换的研究仅有文献[16]从抖动的观点进行了讨论.本文针对事件触发关键级提升后，MC任务可能通过优先级交换获得正确调度的条件进行了分析，并设计了相应的优先级交换算法.

1 任务模型与示例

本节对本文所使用的MC任务模型及相关术语进行定义.引入一个MC任务集运行示例，为后文的优先级可交换分析做准备.

1.1 任务模型

为讨论方便，暂时仅考虑系统只有HI和LO两个关键级的情形.在单处理器平台上，MC任务集τ由互不相关、允许抢占的有限个同步周期任务组成：τ{τ1,τ2,…,τm}，其中m表示任务个数.以执行时间为关键参数，定义任务τi,Ti,Di,li)，其中是任务τi在LO模式时的是在HI模式时的WCET.从保守验证的角度而言，和分别是任务τi在LO和HI模式下能够获得的最大执行时间预算.虽然一个实时任务的实际执行时间是无法预知的，但总是不超过其WCET.即，对于LO任务而言有，对于HI任务则有在LO模式时，在HI模式时且.Ti和Di分别是任务τi的周期和相对截止时限，其值在任何关键级均不变化，且Di≤Ti.当任务τi的关键级li=HI时，表示其为HI任务，其≤Di；若li=LO，则表示任务τi是LO任务.当系统处于HI模式，不确保其正确执行，因此LO任务的不设确定值.任务τi的利用率通常使用计算获得.显然在不同关键级模式下，HI任务有不同利用率，LO模式下，有；HI模式下，有.

响应时间是指任务从释放到执行完毕这一段时间间隔[17].常用于分析固定优先级任务可调度性.一般实时任务τi的响应时间为

(1)

其中hp(τi)是指优先级高于任务τi的所有任务.稍后将讨论关键级对于任务响应时间的影响.

在实际嵌入式应用中，尤其是涉及硬实时的应用，具有可预测性的固定优先级调度被使用得更为广泛[11].在无模式切换发生的静态LO模式和HI模式下，可采用Audsley的最佳优先级分配(optimal priority assignment, OPA)算法[18]分配任务的优先级，算法描述如下：

算法1. OPA算法.

输入：系统模式χ、n个待分配优先级的周期任务集τ；

输出：系统模式为χ时，依据优先级从高到低排列的可调度任务序列.

Step1. 总是从最低优先级k开始分配；

Step2. 任取一个li≥χ的任务τi∈τ；

Step3. 若除τi之外，所有lj≥χ的任务τj均先于τi执行，τi的响应时间不迟于其截止时限，即Ri≤Di，则最低优先级k分配给τi，即pi=k，且将τi移出τ，其他任务重复本步骤依次分配从k-1到1的优先级；

Step4. 否则，从τ中重新选择任务重复Step3.

在每一个关键级模式内使用如上OPA算法对任务进行固定优先级分配.OPA算法将确定优先级分配序列的可调度性测试复杂度从n!降低到n(n+1)2.

1.2 动机示例

如表1所示，待调度的混合关键级任务集共包括4个任务，分别属于HI和LO两个关键级.其中，τ1和τ2是HI任务，其在HI模式和LO模式有不同的WCET值；τ3和τ4是LO任务，仅在LO模式时确保执行.设系统最开始运行于LO模式，使用前述OPA算法，这4个任务的优先级分配结果为p3>p4>p1>p2，在LO模式时调度序列如图1所示.

Table 1 An Example of Scheduling Mixed Criticality Task Set

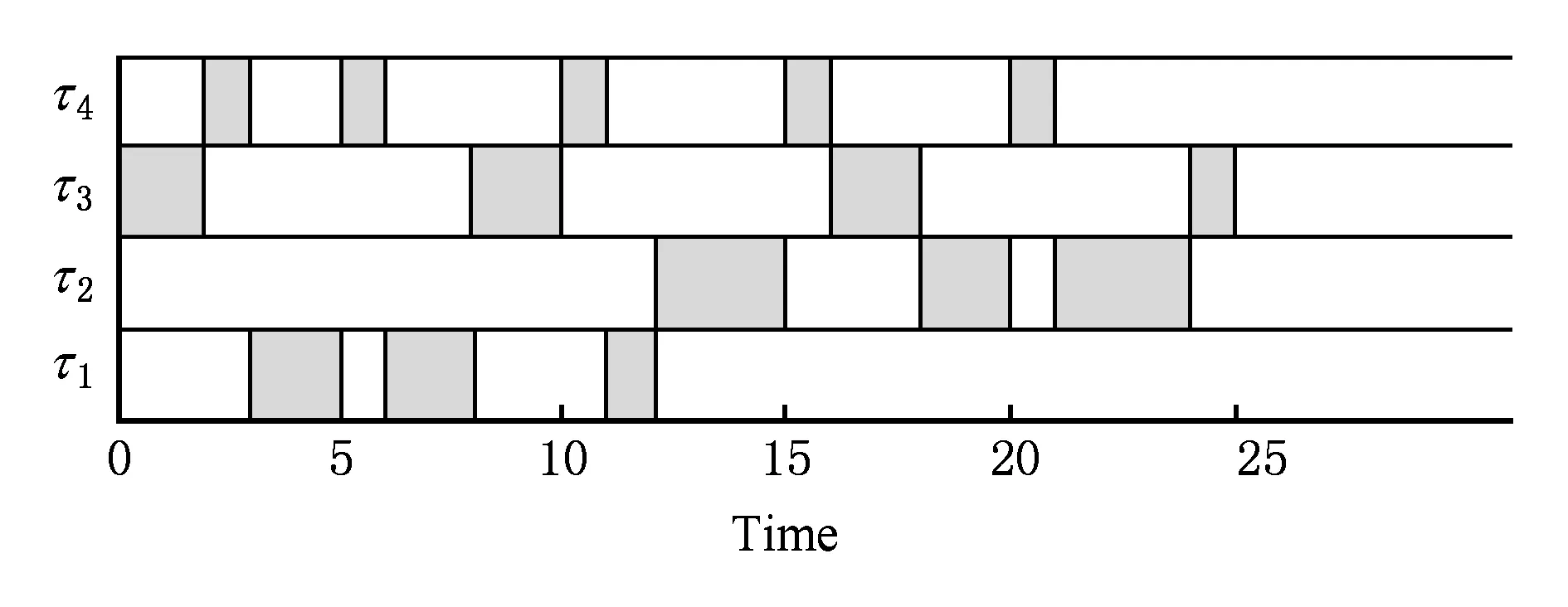
Fig. 1 Scheduling MC tasks in Table 1 in low criticality mode图1 表1示例MC任务集在LO模式的部分调度序列

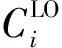
在此例中，可以发现若能在发生模式切换的当前周期内交换2个HI任务的优先级即可以确保满足截止时限.这需要在时刻12之前获知关键级需要提升才能对优先级交换进行预计.由此可见，一个HI任务的截止时限是否能够得到满足，会受到相对较高优先级任务，包括较高优先级的HI任务以及较高优先级的LO任务的影响，也会受到关键级模式切换时刻的影响.

2) 对于HI任务τ2，在执行完毕其低关键级时间预算的时刻，恰好也达到了其截止时限，已获得相对质量较低的执行结果，由于T≥D，在当前周期内任务τ2的此次执行已经结束.

因此，在以执行时间为关键参数的MC系统中，当前常用的以高关键级任务执行时间超过其低关键级WCET的时刻即为关键级提升时刻的设定，可视为是一种延迟关键级模式切换，即直到HI任务达到其CLO时间预算后才进行关键级模式从LO到HI的提升.

下面从外部事件触发关键级提升的观点，对关键级提升期间HI任务的可调度问题以及HI任务之间优先级可交换的问题进行探讨.

2 关键级提升期间的响应时间分析

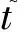
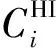
图2所示是一个HI任务τi的执行示例.

Fig. 2 A HI task executing example during a period图2 一个HI任务的执行示例

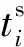
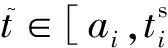
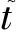
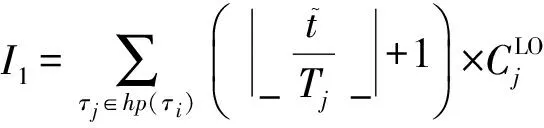
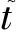
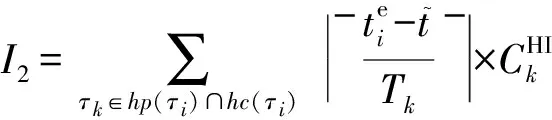
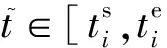
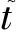
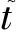
因此，以上2种情形HI任务τi在最差情况下的响应时间为

(2)

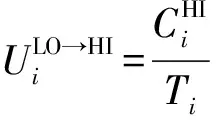
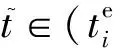
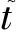
3 关键级提升期内优先级可交换

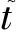
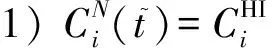
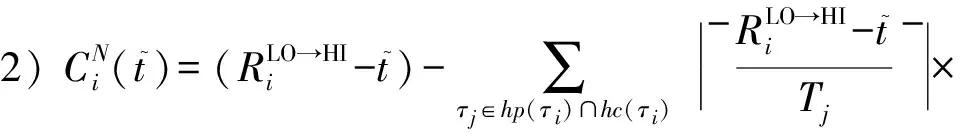
在关键级提升期内，一个RLO→HI>d的HI任务通过与邻近较高优先级任务交换优先级，正如1.2节中例子所示，可能使二者的截止时限均能得到保证.根据固定优先级调度的特点：若较低优先级p=k的任务和较高优先级p=k-1的任务交换优先级执行，对其他任务的调度执行没有影响[19].据此关键级提升期内的优先级交换可尝试在优先级相邻的2个任务间进行.

算法2. 优先级交换(PE)算法.

输入：依据优先级递减顺序排列的在关键级提升期未满足调度条件的HI任务子集τ′、可调度的HI任务子集τo；

输出：依据优先级降序排列的可调度的HI任务子集new_τo.

Step1. 取τo中优先级最低的任务τk，其优先级pk=k；

Step2. 取τ′中优先级最高的任务τi，则其优先级为pi=k+1；

Step5. 更新τi的响应时间为

Step6. 更新τk的响应时间为

Step8. 否则，取优先级为p=k-1的HI任务重复Step3～Step7.

4 仿真与评估

本节对第2节和第3节基于外部事件引发关键级提升的MC系统的可调度性进行测试，并对优先级可交换的算法进行了仿真验证.

4.1 生成测试任务集

借鉴当前MC调度研究的大多数仿真所采用的任务生成方式，使用文献[8]的方法，测试中所使用的待调度MC任务如下随机产生：

1) 对于任务利用率Ui，使用UUnifast算法[21]在0.025～0.975之间产生均匀分布的利用率值；

2) 对任务周期Ti，根据对数正态分布生成任务周期，最小和最大任务周期相差100倍，例如最小任务周期为10 ms，最大任务周期为1 s，大部分是硬实时应用的任务均有类似属性；

3) 对相对截止时限Di，设定Di=Ti；

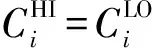
6) 生成的任务由参数cp确定其可能为HI任务的可能性，例如cp=0.5.

4.2 可调度性测试

文献[9]认为一旦HI任务执行超过LO模式时的WCET，即认为是关键级提升的时刻出现，其混合关键级调度算法AMC的结果将作为我们主要的比对、分析对象.

1) AMC.某一个HI任务超出LO模式WCET时，即认为系统关键级提升的时刻出现.

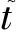
依据4.1节中的方法共计产生1 000个待调度的任务，其中一半为HI任务(cp=0.5)，每个HI任务在HI模式时的WCET是其LO模式时WCET的2倍(cf=2.0).

分别使用AMC和MC-et对上述任务集进行可调度测试，图3显示了可调度任务比率的对比.可以观察到同样是只关注关键级提升后的HI任务的正确执行，MC-et可调度的HI任务比率要高于AMC，且AMC能够调度的任务MC-et均能够调度，反之却不一定.

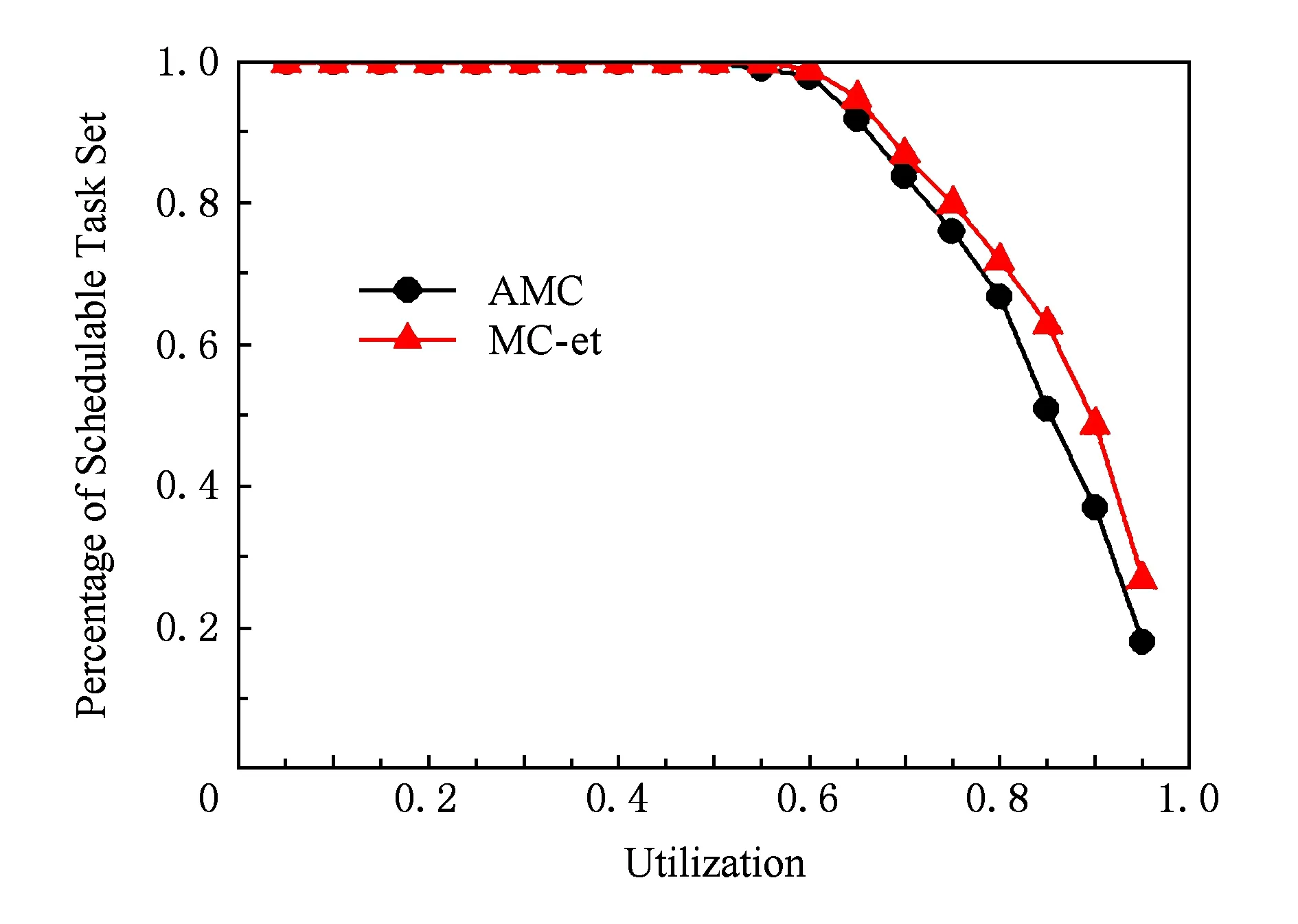
Fig. 3 Percentage of schedulable tasks图3 可调度任务占总任务数的百分比

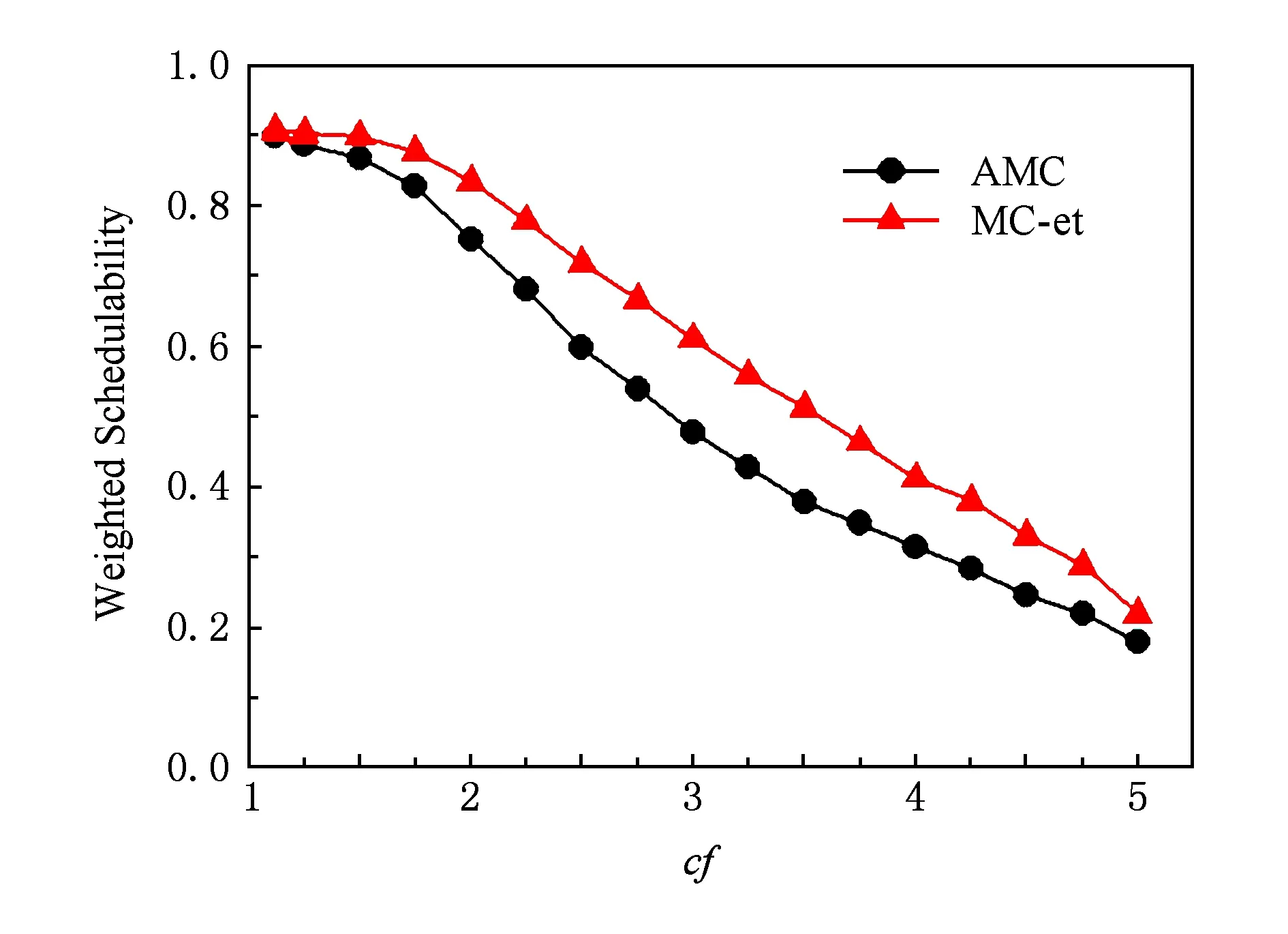
Fig. 4 Varying cf to change the value of affecting schedulable tasks图4 调整参数cf来改变值的可调度任务比率

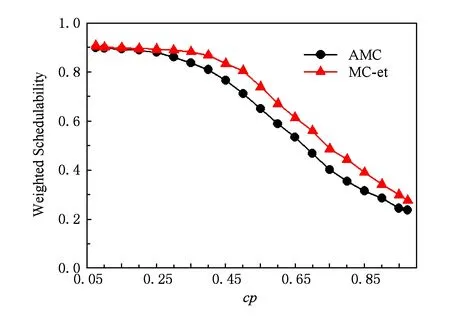
Fig. 5 Varying cp to change the number of HI tasks affecting schedulable tasks图5 调整参数cp来改变HI任务数目的可调度比率

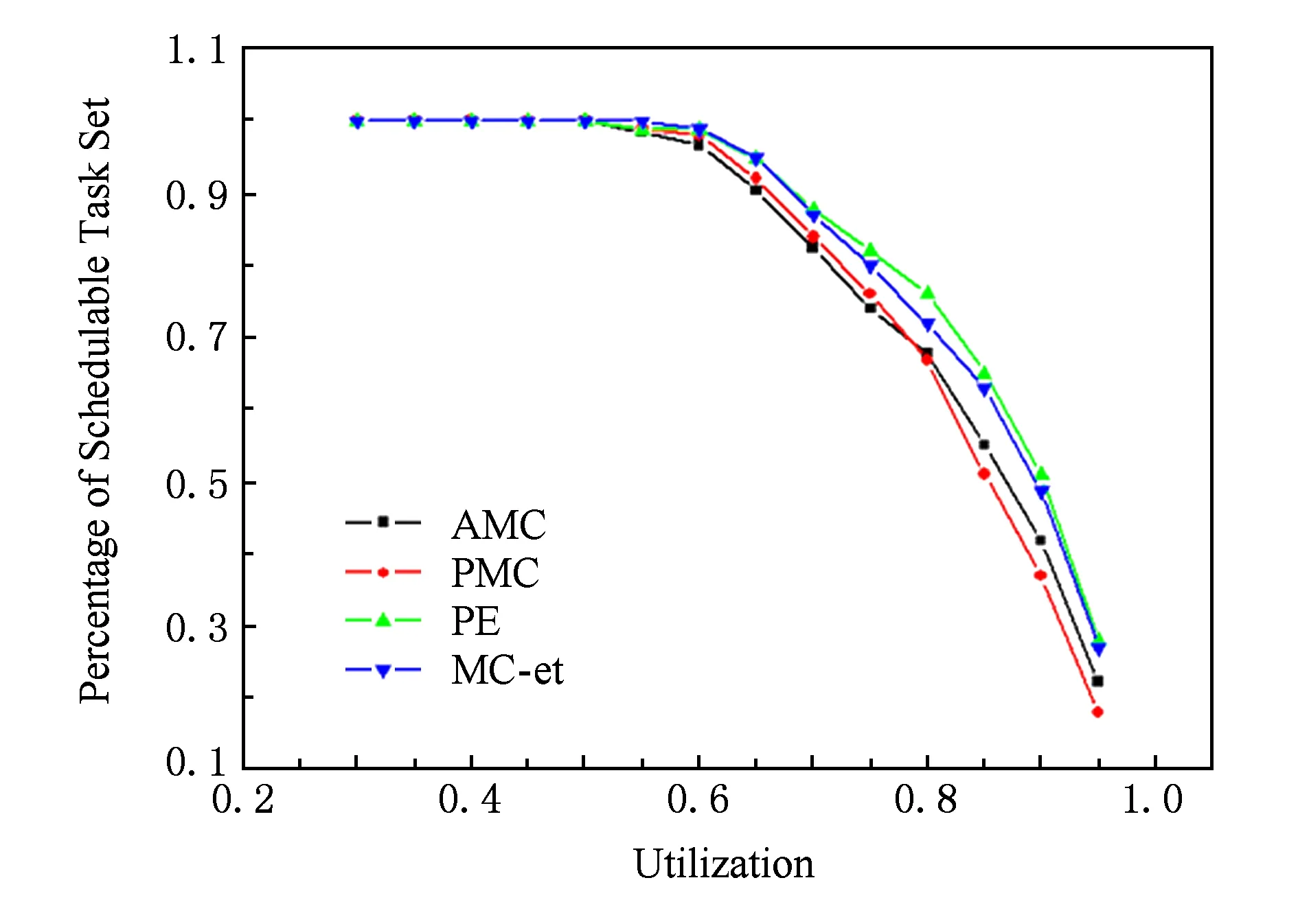
Fig. 6 Exchanging the priorities between MC tasks affecting schedulable tasks图6 交换优先级对可调度任务比率的影响

4.3 优先交换算法的有效性测试

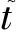
Fig. 7 Exchanging the priorities between varying cf of MC tasks affecting schedulable tasks图7 交换优先级对调整cf值的可调度任务比率影响

Fig. 8 Exchanging the priorities between varying cp of MC tasks affecting schedulable tasks图8 交换优先级对调整cp值的可调度任务比率影响

5 结 论

对于混合关键级系统而言，由低关键级模式到高关键级模式的转换不是由任务执行地变化产生，而是由外部事件引发的，关键参数的变化只是关键级提升的表现.在以任务执行时间为关键参数的混合关键级系统中，不论是从确保高关键级任务正确执行的鲁棒性角度考虑，还是从满足保守的统一标准验证的要求考虑，关键级提升可能发生在高关键级任务在低关键级模式下释放后直至当前周期结束的任何时刻.

对于固定优先级的调度方案，基于外部事件触发关键级模式切换的考虑，本文仅关注高关键级任务截止时限的确保，尤其是系统关键级模式提升期间，基于响应时间分析得出了高关键级任务的可调度条件；并对关键级提升期间，可能发生优先级相邻任务交换优先级满足截止时限的条件进行了讨论分析，并设计了优先级交换算法.仿真实验验证了前述分析与算法的有效性.

在后续工作中，将对动态优先级调度方案和多处理器平台上事件触发关键级提升的混合关键级任务调度进行研究.

[1]Burns A, Davis R. Mixed criticality systems—A review[R]. Yorkshire, UK: Department of Computer Science, University of York, 2013

[2]Niz D d, Lakshmanan K, Rajkumar R. On the scheduling of mixed-criticality real-time task sets[C]Proc of IEEE RTSS 2009. Piscataway, NJ: IEEE, 2009: 291-300

[3]Vestal S. Preemptive scheduling of multi-criticality systems with varying degrees of execution time assurance[C]Proc of IEEE RTSS 2007. Piscataway, NJ: IEEE, 2007: 239-243

[4]Lakshmanan K, Niz D d, Rajkumar R. Mixed-criticality task synchronization in zero-slack scheduling[C]Proc of IEEE RTAS 2011. Piscataway, NJ: IEEE, 2011: 47-56

[5]Baruah S, Li H, Stougie L. Towards the design of certifiable mixed-criticality systems[C]Proc of IEEE RTAS 2010. Piscataway, NJ: IEEE, 2010: 13-22

[6]Burns A, Baruah S. Timing Faults and Mixed Criticality Systems[M]. Berlin: Springer, 2011

[7]Su H, Zhu D. An elastic mixed-criticality task model and its scheduling algorithm[C]Proc of DATE 2013. San Jose, CA: EDAA, 2013: 147-152

[8]Baruah S, Burns A, Davis R I. Response-time analysis for mixed criticality systems[C]Proc of IEEE RTSS 2011. Piscataway, NJ: IEEE, 2011: 34-43

[9]Baruah S, Bonifaci V, D’Angelo G, et al. Mixed-Criticality Scheduling of Sporadic Task Systems[M]. Berlin: Springer, 2011

[10]Schneider R, Goswami D, Masrur A, et al. Multi-layered scheduling of mixed-criticality cyber-physical systems[J]. Journal of Systems Architecture, 2013, 59(10): 1215-1230

[11]Buttazzo G C. Hard Real-Time Computing Systems: Predictable Scheduling Algorithms and Applications[M]. New York: Springer Science & Business Media, 2011

[12]Santy F, George L, Thierry P, et al. Relaxing mixed-criticality scheduling strictness for task sets scheduled with FP[C]Proc of IEEE ECRTS 2012. Piscataway, NJ: IEEE, 2012: 155-165

[13]De-Niz D, Phan L T X. Partitioned scheduling of multi-modal mixed-criticality real-time systems on multiprocessor platforms[C]Proc of IEEE RTAS 2014. Piscataway, NJ: IEEE, 2014: 111-122

[14]Triquet B. Mixed criticality in avionics[COL]Proc of European Commission Workshop on Mixed-Criticality Systems. 2012 [2012-09-11]. http:cordis.europa.eufp7ictembedded-systems-engineeringpresentationstriquet.pdf

[15]Barhorst J, Belote T, Binns P, et al. A research agenda for mixed-criticality systems[R]. Brookings, Washington DC: Department of Computer Science and Engineering, Washington University in St Louis, 2009

[16]Baruah S, Burns A, Davis R I. An extended fixed priority scheme for mixed criticality systems[C]Proc of IEEE RTCSA 2013. Piscataway, NJ: IEEE, 2013: 18-24

[17]Joseph M, Pandya P. Finding response times in a real-time system[J]. The Computer Journal, 1986, 29(5): 390-395

[18]Audsley N C. Optimal Priority Assignment and Feasibility of Static Priority Tasks with Arbitrary Start Times[M]. York, England: University of York, Department of Computer Science, 1991

[19]Burns A. System mode changes-general and criticality-based[C]Proc of the 2nd WMC 2014. Piscataway, NJ: IEEE, 2014: 3-8

[20]Liu J W S. Real-Time Systems[M]. Upper Saddle River, NJ: Prentice Hall, 2000

[21]Bini E, Buttazzo G C. Measuring the performance of schedulability tests[J]. Real-Time Systems, 2005, 30(12): 129-154

[22]Bastoni A, Brandenburg B, Anderson J. Cache-related preemption and migration delays: Empirical approximation and impact on schedulability[C]Proc of OSPERT 2010. Duesseldorf, Germany: Euromicro, 2010: 33-44

Huang Lida, born in 1978. Lecturer and PhD candidate. Her main research interests include real time scheduling and embedded software.

Li Renfa, born in 1956. Professor and PhD supervisor. His main research interests include computer architecture and computer application technology.

The Schedulable Analysis of Real-Time Tasks After Event-Triggered CriticalityLevel Transition

Huang Lida and Li Renfa

(CollegeofComputerScienceandElectronicEngineering,HunanUniversity,Changsha410082)

Both effective resource utilization and meeting the deadlines of high-criticality tasks are objectives of mixed-criticality systems. Currently, it is considered the moment that any of high-criticality tasks execute for their low-critical worst case execution time without completing the system switch from low to high-criticality mode immediately. However, in real embedded applications, the increasing criticality is event-triggered which includes outer circumstance changing, control switching, and so on. That is why the time of raising criticality level can be occurred before, during, or after a task implementation. In this paper we center on that the time of event-triggered increasing criticality is how to influent the scheduling of high-criticality and fixed priority periodic tasks, which is based on the response time analysis. A sufficient condition of scheduling high criticality tasks is derived. Then we discuss when and how to exchange priorities between two high-critical tasks in order to meet their deadlines at the same time, and propose an algorithm of exchanging priorities. Evaluations illustrate the benefits of the schedulable condition and the priority exchanging algorithm.

criticality; event-trigger; priority; response time; deadline

2015-09-30；

2016-02-23

国家自然科学基金项目(61173036) This work was supported by the National Natural Science Foundation of China (61173036).

TP316.2