界标窗口下数据流最大规范模式挖掘算法研究
2017-02-22闻英友王少鹏
闻英友 王少鹏 赵 宏
1(东北大学计算机科学与工程学院 沈阳 110819)2(内蒙古大学计算机学院 呼和浩特 010021)3 (医学影像计算教育部重点实验室(东北大学) 沈阳 110819)(wangshaopeng1984@163.com)
界标窗口下数据流最大规范模式挖掘算法研究
闻英友1,3王少鹏1,2赵 宏1,3
1(东北大学计算机科学与工程学院 沈阳 110819)2(内蒙古大学计算机学院 呼和浩特 010021)3(医学影像计算教育部重点实验室(东北大学) 沈阳 110819)(wangshaopeng1984@163.com)
首次对界标窗口下数据流最大规范模式挖掘问题进行了研究.为了克服naïve算法在处理该问题时不具有增量计算的缺点,提出了一种基于边界界标窗口技术的数据流最大规范模式挖掘(data stream maximal regular patterns mining based on boundary landmark window, DSMRM-BLW)算法.该算法将数据流上的第1个待处理窗口定义为边界界标窗口,使用naïve算法对其进行处理;之后每个窗口上的最大规范模式都可以基于前一个窗口上的最大规范模式集合增量获得,可以克服naïve算法的缺点.实验结果表明:DSMRM-BLW算法是处理界标窗口下数据流最大规范模式挖掘的有效方法,与naïve算法相比,具有相同的执行结果,但时间与空间效率得到了很大的提高.
数据流;界标窗口;最大规范模式;增量计算;边界界标窗口技术
随着数据流应用的不断增多,挖掘数据流中用户感兴趣的模式已然成为数据流挖掘领域中一类非常重要的问题[1].现有相关研究关注较多的是频繁模式的挖掘[1-5],但这些研究存在一个共同问题就是所挖掘模式的判别标准是它们在数据流区间中的出现次数,而并不是模式本身的出现行为(如模式是否周期性、规律性地出现),所以对于很多更注重模式出现行为的实际应用来说,这些研究无法有效解决它们当中所涉及到的问题.比如在超市等销售行业中,管理人员要获得一年中常态情况下货物的销售情况,这种常态通常是指货物的销售具有规律性、周期性且销售的周期不长.如果我们使用挖掘频繁模式的方法来处理这个问题,对于像夏天的电扇和蚊香、冬天的电热宝、雨季的雨具等在一年中某些特定时段内销售频繁的货物,也会因为达到频繁标准而被选择出来,但显然它们并不是一年中满足常态销售这样条件的货物,所以并不是此时我们关注的对象.像实例中这样要求出现具有规律性、周期性的模式通常被称为规范模式(regular pattern)[6-12].而类似应用场景的存在也使挖掘规范模式的研究显得非常必要.
根据模式规范度的度量标准不同,现有规范模式可分为2类:1)以模式发生周期序列中的最大值作为规范度的规范模式;2)以模式发生周期序列的方差作为规范度的规范模式.比较起来前者更有时间优势,而后者精确度更高.Tanbeer等人在文献[1]中对数据流环境下第1类规范模式的挖掘问题进行了研究,给出了基于RPS-tree的处理算法;接着Tanbeer等人又在文献[6]中对规范模式的增量挖掘处理机制进行了研究,提出了一种基于IncRT树的规范模式挖掘算法,只需单遍扫描所关注的数据内容就可以构建IncRT树,接着基于该树以模式增长的方法获得规范模式;Kumar等人在文献[7]中对于数据流环境下基于窗口的第1类规范模式挖掘算法进行了研究,提出了VDSRP算法,该算法采用垂直数据格式组织窗口中的数据,通过类Aprior方法搜索可能的结果模式,在这个过程中通过比较这些模式规范度与用户给定的规范阈值来确定该模式是否是规范模式,能够有效地处理滑动窗口下数据流的规范模式挖掘问题;Verma等人在文献[8]中对VDSRP算法进行了改进,主要改进点在于进一步使用了bit-sequence来组织窗口中的数据,基于窗口中项的bit-sequence执行位操作来获得相关模式规范度,提高了算法执行效率.很多研究还把这类规范模式与频繁模式二者结合起来.如Kumar等人在文献[9]中给出了滑动窗口下基于该规范度的数据流规范频繁模式挖掘方法RFPDS算法,该算法采用垂直数据格式组织窗口中的数据,只计算频繁模式的规范度,通过与用户给定的规范阈值进行比较来确定该模式是否是规范频繁模式,能够有效地处理滑动窗口下数据流的规范频繁模式挖掘问题.Sreedevi等人在文献[10]中首次提出了用于处理滑动窗口下基于该规范度的数据流规范闭模式挖掘算法,该算法将整个规范频繁闭模式的求解过程分为2个阶段:第1个阶段求解规范模式集合;第2个阶段在此基础上得到规范频繁闭模式,可以有效处理这类问题.当前有关第2类规范模式的研究是将规范模式与频繁模式结合起来展开.如Rashid等人在文献[11]中对静态数据库下基于这种规范度的规范频繁模式挖掘问题进行了研究,并给出了相应的处理方法,该方法中使用基于成员出现频率递减顺序的RF-tree来存放数据库中成员信息,另外使用类FP-growth算法的方式挖掘树中的规范频繁模式;Rashid等人在文献[12]中设计了用于寻找传感网络中规范频繁传感器模式的RSP-tree数据结构,使用模式出现周期序列的方差作为模式的规范度,并给出了相应的挖掘算法,能够有效地应用于该领域规范频繁传感模式的挖掘.
由文献[1,13]可知,规范模式具有向下闭包的特点,即如果一个模式是规范的,那么它所有的非空子模式也都是规范的,所以在挖掘数据集中的规范模式时,如果我们只定性地关注哪些模式是规范的而不在意它们的具体规范度,那么完全可以通过挖掘其中所有长度最大的规范模式来提高挖掘效率.这些长度最大的规范模式间彼此并不包含,但能保证数据集中任何一个规范模式都是这些长度最大规范模式集合中某个成员的子集,我们把这类长度最大的规范模式称为最大规范模式.由规范模式的闭包性可知一个数据集上所有的最大规范模式隐含了这个数据集上所有的规范模式,但数量却比全部规范模式要少,这点与频繁模式和最大频繁模式间的关系类似.但由前面分析可知,当前还没有这个方向的研究.
本文基于这点,首次对以模式周期最大值作为规范度的界标窗口下数据流最大规范模式挖掘问题进行了研究.为了能增量地处理这个问题,本文分析了相邻窗口上最大规范模式间的关系,提出了边界界标窗口技术,接着在此技术基础之上给出了该问题的增量处理方法DSMRM-BLW(data stream maximal regular patterns mining based on border landmark window)算法,一系列公用数据集上的实验证明了该算法的有效性.
1 相关知识
1.1 IncRT算法
IncRT算法是由Tanbeer等人在文献[1]中提出的一种目前唯一用于增量挖掘数据库中规范项集(或规范模式)的方法.该方法可以在当前数据库成员规范项集集合的基础上增量获得新数据成员到来后的数据库中规范项集集合.整个算法通过1个IncRT树来维护数据库中的成员信息,该树以字典顺序存放每一条数据记录.树中每条记录的尾结点存放着该记录在数据库中的索引号,以此标识该记录在数据库中的发生情况.树中还维护着1个增量规范表IncR-table,每个表项分为5个域,i域用于存放树中项的名称,IncR-table中该域中成员的排列顺序与树中项的排列顺序相同;r域是该项在树中的规范度;tl域是该项最近发生的记录索引;m域是该项的修改标识域;p域是1个指针域,用于指向树中具有相同项名的结点,树中所有具有相同项名的结点间也有指针彼此连接.在IncRT的构造过程中,头表中除了项的r域外,其他域值都可以设定.当树构造完成后,借助为每个项分配的临时数组结构,按照由下而上的顺序完成对树的1次扫描后得到每个项的r域值.当树的构造完成后,按照FP-growth模式增长挖掘技术来获得所有规范项集,保留所有规范项集成员.之后重置头表成员的m域值.接着把新到来的数据成员插入到IncRT中,这个过程中重新设定头表中成员的m域值;对于新的IncRT,只对IncR-table中m域发生变化的项使用FP-growth算法进行挖掘,假设得到的规范项集集合为A.对于前一个窗口上的规范项集集合,找到其中不包含IncR-table中m域发生变化项的项集,如果在更新它们规范度后得到的规范项集集合为B,则A∪B即为当前数据库上的规范项集集合.有关该算法更详细的说明可参见文献[6].
1.2 PA算法
PA算法是由Verma等人在文献[8]中提出的一种对数据流滑动窗口下以项集周期最大值作为规范度的规范项集(或规范模式)进行挖掘的算法.该算法使用垂直格式组织窗口中的数据流成员,不仅如此,该算法还基于当前窗口中每个项在窗口数据流成员中的出现状况,定义了这些项在当前窗口中的bit-sequence.基于这些bit-sequence,PA算法采用Aprior算法思想可以求得当前窗口中所有项集的bit-sequence.因为基于bit-sequence中非0成员的位置情况,可以得到对应项集在当前窗口中的规范度,所以该算法可以求得当前窗口中所有项集的规范度,进而得到所有规范项集.关于该算法更详细的情况,可参考文献[8].
2 基本概念和问题说明
2.1 基本概念
设SI={I1,I2,…,Im}是m个项的集合,Ii是第i个项,I中的所有成员按全序(字典序)排列.任给集合P,如果P⊆SI且l=|P|(即P中含有l个SI的成员),则称P为l模式,P的长度为l.ST={T1,T2,…,Tn}是事务集,其中Ti⊆SI,也即Ti为SI的子集.
定义1. 模式发生周期[1].任给模式P,令Ti,Tj是事务集ST中2个包含P的事务,且在Ti与Tj间没有任何包含P的其他事务存在,则i与j的差值被称为P的一个发生周期.
定义2. 模式发生周期集合[1].令SP是ST中所有包含模式P的事务集合,|SP|是SP中的事务总数,这里规定null事务(该事务为ST中第0个事务,索引值为ST中第1个事务的索引值-1)和ST中最后一个事务分别是SP中的第1个和最后1个事务,它们和ST中其他所有包含P的事务一起构成了SP,SP中所有事务按它们在ST中的索引递增排列.如果设Trank与Trank+1分别是SP中任意2个相邻事务,它们在ST中的索引分别为Trank.index与Trank+1.index,则CP={Trank+1.index-Trank.index|1≤k≤|SP|-1,k∈+}是P在ST中的发生周期集合.
定义3. 规范模式[1].模式P在ST中的规范度被定义为CP中成员的最大值,表示为RP,即有RP=max(CP).对于用户给定的最大规范阈值λ(1≤λ≤|ST|),如果RP≤λ,则P是ST中一个规范模式;如果P的长度为1,则P又被称为ST中的一个规范项.
定义4. 最大规范模式.对于模式P,如果满足条件Rp≤λ,同时对于任意满足条件Y⊆SI且P⊂Y的模式Y,均有RY>λ成立,则称P为ST上的最大规范模式.
定义5. 数据流DS[1].数据流DS是一个由连续到来的事务组成的事务序列,表示为DS={T1,T2,…,Ti,…}.Ti为第i个到来的事务.
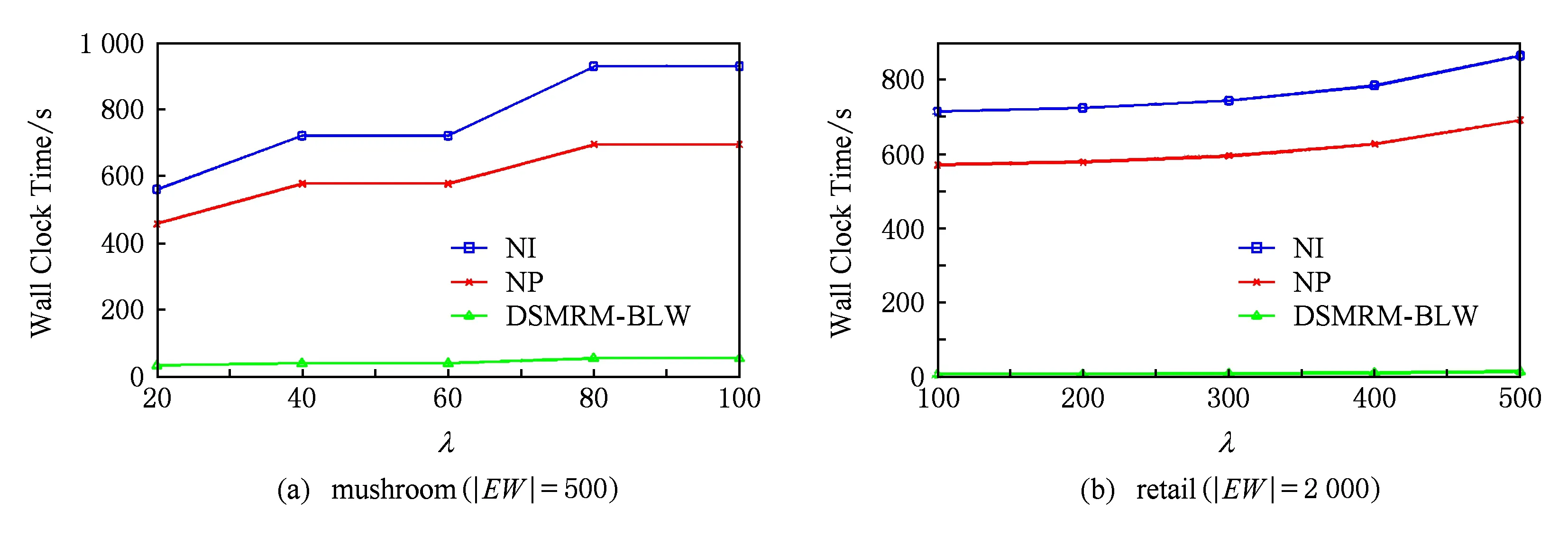
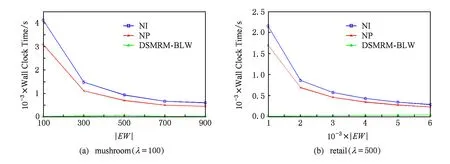
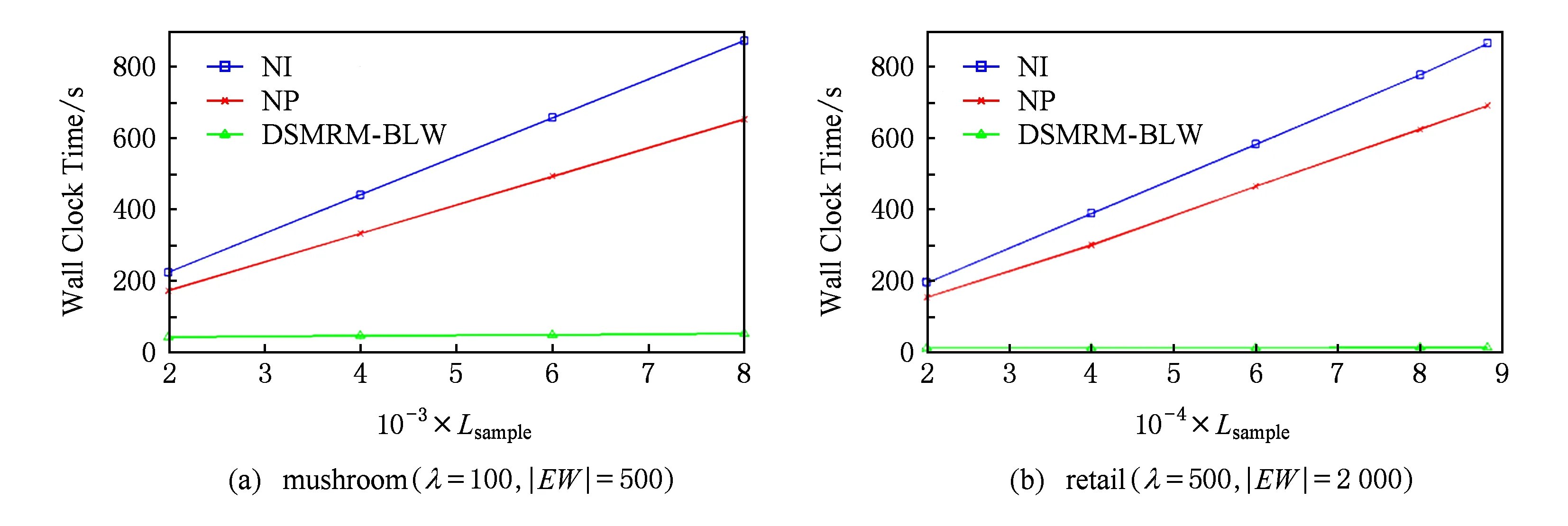
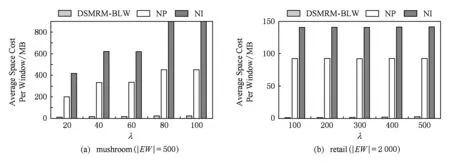
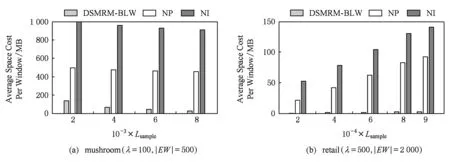
定义6. 基本窗口(element window,EW)与界标窗口(landmark window,LW).EW是一个确定时间内连续到达的数据流成员,即EW={Ti,Ti+1,…,Tj}(0 2.2 问题说明 参照文献[6]中关于增量挖掘规范模式的说明,我们可以给出本文要处理问题的说明,即给定数据流DS、基本窗口大小|EW|、最大规范阈值λ(1≤λ≤|EW|)、界标窗口起始位置sp,本文要解决的问题就是获得起始位置为sp的每个界标窗口上所有的最大规范模式. 当前并没有针对以模式周期最大值为规范度的界标窗口下数据流最大规范模式挖掘的专门研究,所以最直接的处理方式就是从定义出发来解决这个问题.文献[6]中的IncRT算法是目前唯一可用于解决以模式周期最大值为规范度的界标窗口下数据流规范模式增量挖掘的算法,基于该算法与最大规范模式的定义可以得到解决界标窗口下数据流最大规范模式挖掘的算法.文献[8]中的PA算法使用了另外一种不同方法来挖掘滑动窗口中数据流的规范模式.该算法使用垂直格式来组织当前窗口上的数据流成员,并为窗口中的每个项定义bit-sequence,然后采用类Aprior方法来得到当前窗口上的所有规范模式.如果在PA算法的滑动窗口成员更新步骤中只执行加入新数据成员的操作,之后对新窗口中成员再使用PA算法进行处理,那么基于这个改动的算法和最大规范模式的定义,可以得到另外一种挖掘界标窗口下数据流最大规范模式的算法. 以上2种算法在挖掘界标窗口上数据流最大规范模式的过程中,都会执行2个基本操作:1)得到每个界标窗口上数据流的规范模式集合;2)消除集合中成员间存在的超集关系.我们把这2种算法都归类于naïve算法,其中基于IncRT算法的方法被称为NI(naïve based on IncRT)算法,而基于PA算法的方法被称为NP(naïve based on PA)算法.但这2种算法存在明显问题,就是每个界标窗口上(以下简称窗口)最大规范模式集合都需要重新挖掘,而且必须是在得到了所有规范模式之后,才能得到最大规范模式集合,所以时间开销会很大.如果我们能得到相邻2个窗口上最大规范模式间的关系,每次窗口上最大规范模式的求解都是基于前一个窗口上的结果来执行,那么一方面我们无需在求得数量庞大的所有规范模式后再得到最大规范模式集合;另一方面也可以省去对于相邻窗口上相同最大规范模式的重复挖掘,能够减小时间开销.基于这个思想,在这部分我们首先分析了相邻窗口上规范模式间的关系;接着在此基础上得到了相邻窗口上最大规范模式间的关系(我们称其为边界界标窗口技术);随后又给出了便于该技术实现的数据结构;最后在该数据结构的基础上得到了能够增量挖掘界标窗口下数据流最大规范模式的DSMRM-BLW算法. 3.1 相邻窗口上规范模式间的关系 设LWi是第i个界标窗口,RSi与USi分别是LWi上的规范模式与非规范模式集合,|RSi|与|USi|分别是这2个集合中的成员个数,ri,j与ui,j分别是RSi与USi中第j个成员. 性质1. 设Tnew,k是LWi后的第k(k>0)个新到事务,则有USi中任意成员ui,j(1≤j≤|USi|)一定也是LWi∪Tnew,1∪Tnew,2∪…∪Tnew,k上非规范模式集合中的成员. 证毕. 性质2. 设Tnew,k是LWi后第k(k≥1)个新到事务,Tnew,k.index是Tnew,k在数据流中的索引,LWi.sp是界标窗口起始位置的索引.当Tnew,k.index-(LWi.sp-1)>λ时,LWi∪Tnew,1∪Tnew,2∪…∪Tnew,k上的规范模式集合相对于LWi∪Tnew,1∪Tnew,2∪…∪Tnew,k-1上的规范模式集合,没有新模式加入. 证明. 基于规范模式定义可以这样理解LWi上规范模式的挖掘过程.首先针对LWi中每个事务求得该事务包含的所有子模式(即由构成该事务的项形成的所有子集),每个子模式的索引都为该事务的索引,这样由产生于每个事务的所有子模式构成了候选规范模式集合CSi;接着求CSi中每个模式的规范度;最后通过规范度与最大规范阈值λ的比较判断该模式是否为规范模式.当k=1时,令由Tnew,1产生的所有子模式所构成的集合为Subsetnew,1.则Subsetnew,1与LWi上的候选规范模式集合CSi构成了LWi∪Tnew,1上的候选规范模式集合.假设在Tnew,1到来后有新规范模式r1产生,则该r1一定位于Subsetnew,1中,而并不位于CSi中.这是因为如果r1也存在于CSi中,由题设可知,r1在CSi中并不是规范模式,也即r1在LWi上的规范度大于λ;当Tnew,1到来后,因为r1变成了规范模式,所以r1在LWi∪Tnew,1上的规范度小于等于λ.但因为LWi⊂(LWi∪Tnew,1),再结合定义3可知,r1在LWi∪Tnew,1上的规范度一定大于等于其在LWi上的规范度,也即大于λ,这与r1是LWi∪Tnew,1上的规范模式相矛盾,所以r1不存在于CSi中.这样r1的索引一定为Tnew,1.index.当Tnew,1.index-(LWi.sp-1)>λ时,由规范度定义可知,此时有Rr1>λ,故r1并非规范模式,这也与假设矛盾,即在Tnew,1到来后没有新规范模式产生.与k=1的证明相类似,容易推得当k≥2时,结论也成立. 证毕. 下面我们通过实例说明性质1~2的内容.图1给出了1个数据流图示,其中|EW|=3. Fig. 1 Illustration of the property 1 and property 2图1 性质1和2的说明 图1中ID为4的Transaction(图1中加重且有下划线的事务,记为T4)是界标窗口LW1后的第1个事务,由定义2~3可知,E在LW1中的规范度RE=2.当λ=1时,E是LW1上的非规范模式,这时考虑E在LW1∪T4上的规范性,由性质1可知,E一定是LW1∪T4上的非规范模式;当λ=3时,考虑LW1∪T4上的规范模式,因为此时有T4.index-(LW1.sp-1)=4-(1-1)=4>λ,所以由性质2可知,LW1∪T4上的规范模式集合与LW1上的规范模式集合相比,没有新模式加入.同样由性质2可知,LW1∪T4∪T5∪T6…上的规范模式集合与LW1上的规范模式集合相比,没有新模式加入. 3.2 边界界标窗口技术 定义7. 边界基本窗口(border element window, BEW)与边界界标窗口(border landmark window, BLW).令界标窗口LW的起始位置为LW.sp,Tran是起始位置后的1个事务,Tran.index是该事务在数据流中的索引.如果Tran满足条件Tran.index-(LWi.sp-1)=λ,我们就把Tran所在的基本窗口定义为边界基本窗口BEW,而以BEW为最后一个基本窗口的界标窗口定义为边界界标窗口BLW. 性质3. BLW后的任意一个界标窗口,其上的规范模式集合与相邻前一个界标窗口上的规范模式集合相比,没有新模式加入. 证明. 由性质2容易推得该性质成立. 证毕. 性质4. 假设ms是BLW上的最大规范模式.考虑BLW后第1个界标窗口NLW1,有3个结论成立: 1) 如果ms是该窗口上的规范模式,则ms一定也是该窗口上的最大规范模式. 2) 如果ms不是该窗口上的规范模式,且其中每个成员都是规范项,设ms长度为len,将ms所有len-1模式中满足规范条件的成员放入结果集合;然后针对每个不满足规范条件的len-1模式,求它们的len-2模式,将所有len-2模式中满足规范条件的成员放入结果集合,这个过程一直到产生的每个模式都满足规范条件或者是执行到所有1模式为止,如果对此时结果集合执行超集检测后得到的集合为NS,则NS是当前窗口上ms所有子模式的最大规范模式集合. 3) 如果ms不是该窗口上的规范模式,且其中存在非规范项.这时令执行了非规范项删除操作后的ms为ms1,当ms1是规范模式时,该模式也是当前窗口中ms子模式的最大规范模式;否则按结论2对其进行处理,能得到当前窗口上ms所有子模式的最大规范模式集合. 证明. 1) 设BLW与NLW1上的规范模式集合分别是RS1与RS2.因为ms是BLW上的最大规范模式,所以由定义4可知我们无法在RS1中找到1个成员rs满足条件ms⊂rs.考虑NLW1上情况,如果ms同时也是NLW1上的规范模式,也即ms满足条件ms∈RS2,这时因为无法在RS1中找到1个成员rs满足条件ms⊂rs,而且由性质3可知RS2⊆RS1,所以也无法在RS2中找到成员rs1满足条件ms⊂rs1,也即ms是NLW1上的最大规范模式. 2) 因为ms是BLW上的最大规范模式,由规范模式闭包性可知,ms所有子模式也都是规范模式,而且ms能覆盖(覆盖是指子模式中的所有项都在ms中)这些子模式.另外由性质3可知RS2⊆RS1,所以ms也能覆盖存在于RS2中ms的所有子模式.但因为ms∉RS2,所以ms并不是存在于RS2中ms子模式的最大规范模式.设ms长度为len,由Aprior算法可知,ms可由ms的len-1模式执行连接操作来得到,而且ms可以覆盖它的所有len-1模式.依次类推,可得ms的所有len-1模式覆盖了除ms外所有的ms子模式.所以当ms不是NLW1上的规范模式时,这时判断ms上的len-1模式,如果它们都是规范模式,也即它们都是RS2中的成员,那么因为此时ms∉RS2,所以由这些规范模式构成了能够覆盖存在于RS2中ms子模式的最大规范模式集合.如果其中存在某个len-1模式不满足规范条件,则使用相同方法判断该模式的len-2模式,一直到关注的每个模式都满足规范条件,则由所有获得的规范模式构成了结果集合.由定义4可知,在消除了集合中成员间存在的超集关系后,该集合即为能够覆盖存在于RS2中ms子模式的最大规范模式集合. 3) 假设F是ms在NLW1中任意非规范项,由规范模式闭包性可知,F在ms中的任何超集都不可能是NLW1上的规范模式,所以ms上含有F的子模式都不可能是NLW1中的规范模式,即RS2中不存在ms上含有F的子模式.假设subsetms是ms的子模式集合,则ms能覆盖subsetms中每个成员;考虑存在于RS2中的ms子模式集合subset1ms,由前面分析可知subset1ms⊆subsetms成立,所以ms同样可以覆盖subset1ms中的每个成员;从subsetms中删除所有含有ms在NLW1中非规范项的子模式,我们把新得到的集合记为subset2ms,则有subset1ms⊆subset2ms.另外假设ms在执行了删除所有NLW1中非规范项的操作后变为ms1,则ms1能够覆盖subset2ms中的所有成员,进一步可以覆盖subset1ms中的所有成员.当ms1为NLW1上的规范模式时,结合定义4可知,ms1是subset1ms中的最大规范模式;当ms1是NLW1上的非规范模式时,与证明2情况类似,易得结论成立. 证毕. 性质5. 假设BLW上最大规范模式集合mset={ms1,ms2,…,msn},NLW1上最大规范模式集合为mset1.对于mset与mset1有2个结论成立: 1) 如果mset中每个成员仍是NLW1上的规范模式,则mset=mset1. 2) 如果mset中有些成员不是NLW1上的规范模式,此时mset中的成员可分为3类:①在NLW1上仍然是规范模式的成员;②在NLW1上不是规范模式,但模式的构成项中都是规范项的成员;③在NLW1上不是规范模式,但模式构成项中存在非规范项的成员.分别使用性质4的结论1~3来处理上述3类成员,假设由这3类成员的处理结果构成的集合为RS,则执行了超集检验后的RS即为当前窗口上的最大规范模式集合. 证明. 1) 设RS1与RS2分别是BLW与NLW1上的规范模式集合.因为mset是BLW上的最大规范模式集合,所以可知:①mset中的成员覆盖了RS1中的所有规范模式;②mset中任意2个成员msk与msl都有如下关系msk∩msl≠msk,且msk∩msl≠msl成立;③对于mset中任意成员mst,我们在RS1中无法找到1个成员rs,使得条件mst⊂rs成立.如果mset中每个成员仍是NLW1上的规范模式,由性质4的结论1可知,这些成员也是NLW1上的最大规范模式,即mset也是NLW1上最大规范模式的集合.又由性质3可知RS2⊆RS1,而且再由前面①可推得mset中的成员也覆盖了RS2中的所有规范模式,另外前面的②和③显然在NLW1上也依然成立,即mset也是NLW1上的最大规范模式集合. 2) 由证明1可知,如果mset中每个成员仍是NLW1上的规范模式,则mset=mset1,结合定义4可知,对于NLW1上任意1个规范模式,在mset(此时也即mset1)中至少有1个成员会完成对该模式的覆盖.假设此时mset中有M个成员,我们可以根据RS2中成员(即NLW1中规范模式)被这M个成员所覆盖情况,将其中成员分为M类,当然这M类成员彼此间可能会有重合.每一类中成员都被对应mset中的成员所覆盖.当mset中某些成员并不是NLW1上的规范模式时,NLW1上本来应该由这些成员覆盖的所有规范模式,此时可能就没有最大规范模式覆盖了,所以需要求这部分规范模式的最大规范模式.假设将mset中不是NLW1上规范模式的成员组合成集合nset,对于nset中任意成员nseti,如果nseti的构成项都是规范项,由性质4的结论2可知,使用该结论处理nseti后可以得到集合NSi,该集合是NLW1上nseti所有子模式的最大规范模式集合,覆盖了存在于RS2中nseti的所有子模式;如果nseti的构成项中存在非规范项,由性质4的结论3可知,在使用该结论处理nseti后,也可以得到该成员在NLW1上所有子模式的最大规范模式集合,覆盖了存在于RS2中nseti的所有子模式;设从mset中除去nset中的成员后得到的集合为mset|nset,由前面分析及由性质4的结论1可知,这些成员也是NLW1上的最大规范模式,可以覆盖存在于RS2中每个mset|nset中成员的所有子模式,所以由这3部分构成的RS覆盖了RS2中所有规范模式,由定义4可知,RS集合在执行超集检测后,即成为NLW1上的最大规范模式集合. 证毕. 我们仍以图1为例说明这些性质内容.设LW1上λ=3时的规范模式集合为RS,由图1可知RS={A,B,C,D,E,F,AC,AD,AB,AE,AF,BC,BE,BF,EF,CE,ABC,ABE,ABF,BCE,BEF,AEC,AEF,ABCE,ABEF};显然最大规范模式集合MRS={ABCE,ABEF,AD};在求LW2上最大规范模式时,如果ABCE,ABEF与AD仍是LW2上的规范模式,则LW2上的最大规范模式集合仍然为{ABCE,ABEF,AD}(性质5的结论1).因为ABCE与ABEF都是LW2上的规范模式,所以它们仍然是LW2上的最大规范模式(性质4的结论1);又因为AD不是LW2上的规范模式,而且这时D不是LW2上的规范模式,所以这时只考虑A.因为A是规范模式,所以A是AD在LW2上所有子模式的最大规范模式(性质4的结论3).令A与ABEF以及ABCE构成集合Stem,由性质5的结论2可知,在对该集合执行超集检测后,可得LW2上λ=3时的MRS={ABCE,ABEF}. 由性质4~5不难推得BLW后任意2个相邻界标窗口上最大规范模式集合间都有相同结论成立.另外由2.2节可知,本文中λ的取值范围为1≤λ≤|EW|,所以本文中BLW为最大规范模式挖掘过程中的第1个界标窗口.由性质5可知,从第2个界标窗口开始,可以基于前一个窗口上最大规范模式集合来获得当前窗口上最大规范模式集合.具体方法为首先考虑前一个窗口上最大规范模式集合中每个成员模式的规范度,如果这些模式规范度都满足规范条件,则它们构成了新窗口上的最大规范模式集合,否则使用性质5中的结论2对其进行处理,则可以得到当前窗口上的全部最大规范模式.这种从边界界标窗口的下一个窗口开始,基于前一个窗口最大规范模式集合求得当前窗口最大规范模式集合的方法被称为边界界标窗口技术. 3.3 数据结构 通过前面对边界界标窗口技术的分析可知,该技术执行的1个重要前提就是需要一种便于计算前一个窗口上最大规范模式在当前窗口上规范度的方法,而这种方法还需要便于计算当前窗口上由规范项所构成的任意模式的规范度.本部分主要给出了相关的数据结构,而这些数据结构的使用可以满足边界界标窗口技术使用的前提条件. 3.3.1BV(bit-vector) table 参照文献[8]中的bit-sequence思想,我们对于边界界标窗口中每个项维护一个bit-vector结构.窗口中所有项的bit-vector构成了bit-vectortable(简称BVtable).因为通过性质3可以知道,BLW后的每个窗口上的规范模式都是BLW上规范模式的子集,进一步可知,BLW后每个窗口上所有规范项的集合都是BLW上所有规范项集合的子集,所以我们只要维护好边界界标窗口上的BVtable在每个新窗口上的状态,无论计算前一个窗口上的最大规范模式在当前窗口上的规范度,还是计算当前窗口上由规范项所构成模式的规范度,只需在当前窗口的BVtable中找到模式中项对应的bit-vector,然后基于它们执行与操作,最后对得到的结果计算规范度即可. 1)BVtable结构 BVtable包含name,bit-sequence,reg,lastpos,sign这5个域,分别对应项的名称、项在当前窗口中的bit序列、项的规范度reg、bit-sequence后|EW|个bit序列中最后一个非0位置以及该项在当前窗口上的规范度是否不大于规范阈值λ的结果.其中bit-sequence是1个长度为|LW|×|EW|的位序列,每一位与界标窗口中的每个数据流成员相对应.如果该项在这个数据流成员中出现,则对应的bit-sequence位设为1,否则设为0.BVtable中每条记录与当前窗口中的每个项对应,该记录也是对应项的bit-vector.BVtable中所有项按字典顺序排列.表1给出了图1中LW1上当λ=3时的BVtable. Table 1 BV table over the LW1 2) 构建BVtable 由定义7分析可知,本文中BLW是界标窗口中第1个窗口,所以BVtable在第1个窗口中成员到来后开始构建.①首先将BLW中的数据流成员按字典顺序转换成垂直格式,完成BVtable中每个项bit-sequence的构造;②将bit-sequence中非0成员位置记录下来形成1个序列,该序列在增加头成员0和尾成员|EW|后形成1个新序列,求该序列中相邻成员差值的最大值,以此作为该项的reg值,同时将bit-sequence中最后一个非0成员的位置作为该项的lastpos;③根据该项reg值与规范阈值λ间的关系,完成sign域的赋值.当完成这些操作后,BLW上的BVtable构造完成.具体如表1所示. 3) 更新BVtable 首先,结合规范模式的性质与BVtable结构特点,可以得到性质6: 性质6. BLW上的BVtable中如果有项A的sign域值为false,则有2个性质成立:①之后每个界标窗口上的BVtable中,该项的sign域值都为false;②BLW上及其之后的每个窗口上的规范模式集合中,都不会有含有该项的模式出现. ② 由规范模式向下闭包性的性质可知,每个界标窗口上都不会有含该项的规范模式出现.性质6中结论②成立. 证毕. 由性质6可知,在我们得到边界界标窗口上的BVtable在每个新窗口上的状态时,我们只需对前一窗口上BVtable中sign域值为true的项执行更新即可. 具体更新过程在新EW中所有成员到达后执行,设前一个界标窗口上的BVtable为PV.首先我们会针对PV中所有sign域为true的项,按照它们在新EW的数据流成员中是否出现的情况,构建这些项在新EW中的bit-sequence(记为item.bit-sequence).同时记下item.bit-sequence中第1个非0成员位置fp和最后一个非0成员位置lp.如果item.bit-sequence=0,我们令fp=|EW|,lp=0;接着按照定义1~3对item.bit-sequence进行处理可以得到该项的reg值,记为item.reg.为便于说明,假设PV中sign域值为true的项I在新EW上的信息组成的临时表为TemI,另设项I在PV中对应的bit-vector为PVI,则可通过3个步骤更新PVI中信息:①PVI.bit-sequence=PVI.bit-sequence∪TemI.bit-sequence;②PVI.reg=max(|EW|-PVI.lastpos+TemI.fp,PVI.reg,TemI.reg);③PVI.lastpos=TemI.lp.表2给出了图1中LW2上当λ=3时的BVtable. Table 2 BV table over the LW2 4)BVtable的结构分析 令item是BLW上任意规范项.由界标窗口特点可知,相邻下一个界标窗口是在当前窗口上加1个基本窗口构成的,也就是任何项在下一个界标窗口上的bit-sequence是由该项在当前窗口上的bit-sequence与其在下一个基本窗口上的bit-sequence构成.设BScur是item在BLW上的bit-sequence,而BSnext是item在NLW1上的bit-sequence,则BScur与BSnext之间除了最后|EW|个位序列,其余完全相同.因为我们要求item在下一个窗口上的规范度,也即基于BSnext求item的规范度,而在处理BLW时我们基于BScur已经得到了item在该窗口上的规范度,所以在基于BSnext求item的规范度时,我们可以先求得BSnext中后|EW|个位序列上的规范度,把这个作为1个最终可能规范度.另外需要注意的是,BSnext的后|EW|中的第1个非0位与前面序列中最后一个非0位之间的差值,也可能是规范度,所以我们设立了lastpos域,我们把这个作为第2个最终的可能规范度.由定义3可知,这2个可能规范度和BScur上规范度3者中的最大值为最终item的reg值.这样就使我们在只关注item在新界标窗口上bit-sequence中的后|EW|个位序列的情况下,能够得到该项在新界标窗口上的规范度.类似地,任意界标窗口上规范项都有这样的规律.而和基于新界标窗口上该项的整个bit-sequence来计算该项的规范度相比,显然现有的方法可以更好地减少运算量. 3.3.2 Hash索引表HIT(Hash index table) 在基于BVtable计算前一个窗口上的最大规范模式在当前窗口上的规范度,或者是求得当前窗口上由规范项所构成的任意模式的规范度时,我们需要随时能得到模式的每个项在当前窗口BVtable中的bit-sequence.如果直接使用BVtable,因为求得每个项在当前窗口中的bit-sequence,实际上都需要对BVtable执行一次扫描操作,所以效率较低.为解决这个问题,我们以项名为key,以项在BVtable中索引位置index为value设计了Hash索引表HIT.通过这个数据结构,我们能以O(1)的时间开销找到当前窗口中任何项在BVtable中的位置,进而得到该项的bit-sequence.图2说明了LW1上λ=3时的HIT与BVtable间的关系. Fig. 2 The relationship between the HIT and the BV table over the LW1图2 LW1上的HIT与BV table间的关系 性质7. 每个窗口上BVtable的HIT都是相同的,无需随着窗口成员的更新而更新. 证明. 由BVtable的更新过程可知,每个窗口上的BVtable中项的个数与位置并不会发生变化,所以与每个窗口上BVtable相关的HIT也不会发生变化,无需随着窗口成员的更新而更新. 证毕. 3.3.3 优化策略 性质8. 在按照边界界标窗口技术求得当前窗口上的最大规范模式集合时,我们需要计算前一窗口上的所有最大规范模式在当前窗口上的规范度.在这个过程中,假设前一个窗口上的最大规范模式中存在着某些成员项,这些项在当前窗口BVtable中的sign域值为false,则我们在处理该最大规范模式时可以忽略对于这些项的处理. 证明. 由规范模式向下闭包性特点,性质4的结论3以及性质5的结论2可得性质8成立. 证毕. 该优化策略可以减少我们在使用边界界标窗口技术求得界标窗口上最大规范模式过程中对于很多不必要成员项的处理,能够提高整个执行过程的时间效率. 我们以LW3上最大规范模式的求解过程为例来说明优化策略的内容,表3是图1中LW3上当λ=3时的BVtable. Table 3 BV table over the LW3 由前面可知LW2上λ=3的最大规范模式集合为RS2={ABCE,ABEF}.又由表3可知A,F在LW3上BVtable中的sign域值为false,所以按照优化策略,当重新计算ABCE与ABEF在LW3上的规范度时,可以忽略对其中A,F的处理.也就是说,只需计算BCE和BE的规范度.对于BCE来说,因为它在LW3上的规范度为4,所以不满足规范条件.按照边界界标窗口技术考虑BCE长度为2的子模式:BC,BE,CE.因为BC的规范度为3,CE的规范度为2,都满足规范条件,所以它们仍是当前窗口上BCE所有子模式的最大规范模式集合中的成员;对于BCE的另一个长度为2的子模式BE,因为它在LW3上的规范度为4,所以不满足规范条件.按照边界界标窗口技术考虑BE的长度为1的项子模式:B,E.显然B,E此时都满足规范条件.令Stem={BC,CE,B,E},按边界界标窗口技术可知,当消除了Stem中成员之间存在的超集关系后,Stem={BC,CE}即为当前窗口上BCE所有子模式的最大规范模式集合;对于RS2中此时需要处理的另外一个模式BE,类似地可以得到S1tem={B,E}为当前窗口上BE所有子模式的最大规范模式集合.同样由边界界标窗口技术可知,假设Stem与S1tem中成员构成了新集合Sfinal,即Sfinal={BC,CE,B,E},那么当消除了该集合中成员间存在的超集关系后,该集合便是LW3上当λ=3的最大规范模式集合RS3,也即RS3={BC,CE}. 3.4 DSMRM-BLW算法 由边界界标窗口技术可知,在使用naïve算法求得第1个界标窗口上最大规范模式集合后,我们可以基于该集合求得相邻下一个窗口上的最大规范模式集合.依次类推,可以得到之后每个界标窗口上的最大规范模式集合.另外通过文献[1,6]可知,NI算法在第1个窗口上的执行效果与文献[1]中的RPS-tree算法相同,又由文献[8]可知,PA算法求得滑动窗口上规范模式的时间开销小于RPS-tree算法.所以我们可以在第1个窗口上执行NP算法,即使用PA算法求得该窗口上的规范模式集合,然后消除该集合成员间存在的超集关系,以此来得到该窗口上的最大规范模式集合,对于之后每一个界标窗口上的最大规范模式集合,使用边界界标窗口技术来获得,我们把这种算法称为DSMRM-BLW算法.另外由前面BVtable结构可知,该数据结构中含有PA算法执行所需的bit-sequence,所以DSMRM-BLW算法在第1个窗口上的执行无需再构造其他数据结构,直接使用BVtable中的bit-sequence即可. DSMRM-BLW算法在前面数据结构的基础上,完成了基于边界界标窗口技术挖掘每个界标窗口上数据流最大规范模式的操作.算法具体描述如下: 算法1. DSMRM-BLW. 输入:数据流DS、界标窗口LW的起始位置sp、规范阈值λ、基本窗口大小|EW|; 输出:每个界标窗口上的最大规范模式集合. ① 从数据流中索引为sp的成员开始,对每个界标窗LW执行如下操作; ② {if (theLWis BLW) ③ {构建BLW上的BVtablecurtable与HIT; ④Sregular=PA(curtable);*使用PA算法 得到当前窗口上完整的规范模式集 合* ⑤ 消除Sregular中任意2个成员间存在的超集关系; ⑥Smaxregular=Sregular; ⑦ outputSmaxregular;*输出BLW上的最大规范模式集合* ⑧ } ⑨ else ⑩ {基于新EW的成员,按照3.3.1节3)的 方法更新curtable; DSMRM-BLW算法在使用边界界标窗口技术求得当前窗口上最大规范模式集合时,如果前一窗口上最大规范模式在当前窗口上不满足规范条件,则需要求得该模式在当前窗口上所有子规范模式的最大规范模式.下面的GetMRM-subset算法给出了具体求解过程. 算法2. GetMRM-subset. 输入:规范阈值λ、在当前窗口上不满足规范条件的前一窗口上最大规范模式eset、当前窗口上的BVtablecurtable; 输出:eset所有子规范模式的最大规范模式集合MRSeset. ① for (eset每个长leneset-1的子集esubset) ② {计算esubset的规范度regesubset; ③ if (regesubset<λ)*判断esubset的规范度regesubset是否小于λ* ④MRSeset←esubset; ⑤ else ⑥MRSeset←GetMRM-subset (λ,esubset,curtable); ⑦ } ⑧ 消除MRSeset中任意2个成员间的超集关系; ⑨ returnMRSeset. 设eset的长度为leneset,对于eset中每个长为leneset-1的子集esubset执行如下步骤:如果esubset满足规范条件,则将该子集放入MRSeset中(行③~④);如果esubset的规范度不满足规范条件,设lenesubset是esubset的长度,则使用相同方法对于esubset的长度为lenesubset-1的子集进行处理(行⑥);当处理完eset中每个长为leneset-1的子集后,只需消除MRSeset中成员间的超集关系,便可得到eset中所有子规范模式的最大规范模式集合MRSeset(行⑧~⑨). 本部分实验主要分3部分:1)实验验证最大规范模式相对于规范模式的优势,这也是本文的研究意义所在;2)验证本文提出的DSMRM-BLW算法在挖掘界标窗口上数据流最大规范模式时的有效性;3)对DSMRM-BLW算法性能进行了评价. 4.1 实验环境 本文全部实验都在一台配置为Intel®coreTMi5 CPU 650 @3.20 GHz CPU、1.12 GHz主频、4 GB内存、Windows XP 的PC机上执行.算法由VC++6.0实现.实验使用了频繁模式挖掘公用数据集中的mushroom和retail数据集.其中mushroom是1个稠密数据集,共有8 124条记录,大小为0.54 MB,item的个数为120,平均记录长度为23(即含有23个item);retail是1个稀疏数据集,共有88 162条记录,大小为3.97 MB,16 470个item,平均每条记录的大小为13;另外在实验中,我们设定界标窗口的起始位置都为数据样本中第1个成员的位置.因为当前并没有关于这个方向的研究,所以实验中的对比算法为前面第3节提到的NI与NP2类naïve算法(其中基于IncRT算法的方法被称为NI算法;而基于PA算法的方法被称为NP算法). 4.2 最大规范模式相对于规范模式的优点 本节就最大规范模式相对于规范模式的优势作了实验验证.具体实验方法是首先对数据样本分别执行NI与IncRT算法以得到最大规范模式集合A与规范模式集合B;接着比较这2个结果集合中成员的内容与数目.为便于说明,我们定义了2个参数:1)Raccommodate,该参数用于表征集合A对于集合B的容纳程度;2)Rreduction,用于描述集合A相对于集合B的约减程度.设|A|与|B|分别表示集合A,B中的成员个数,又设变量Naccommodate表示集合A所容纳集合B中成员的数目,该变量的更新变化规则是,对于集合B中的每个成员elementb,如果能在A中找到一个成员elementa,使得elementb是elementa的子集,则令Naccommodate加1.基于这样的规定,我们可以将集合A相对于集合B的Raccommodate与Rreduction具体定义描述如下: Raccommodate=|Naccommodate||B|, (1) Rreduction= |A||B|. (2) 由上面的定义描述可知,如果实验结果中能够保持Raccommodate=1,且Rreduction<1,则可以说明最大规范模式集合具有全部规范模式集合的信息,同时规模比规范模式集合要小.具体针对不同真实数据样本的实验结果,如图3所示: Fig. 3 The Raccommodate and Rreduction about maximal regular patterns over the regular ones when different data samples are taken图3 不同数据样本下最大规范模式相对于规范模式的Raccommodate与Rreduction 由图3可以看到,在不同数据样本下,最大规范模式集合相对于规范模式集合的Raccommodate始终为1,而Rreduction取值也远小于1.由前面分析可知,这样的实验结果足以说明最大规范模式集合含有规范模式集合所有的信息,同时数量规模上也小于规范模式集合,所以,当我们只想定性地确定数据集中哪些是规范模式,而不关注具体每个规范模式规范度时,挖掘最大规范模式更有效率,这也是本文的研究意义所在. 4.3 DSMRM-BLW算法的有效性 本节实验主要用于验证DSMRM-BLW算法在挖掘界标窗口上数据流最大规范模式时的有效性.这里我们使用的方法是将DSMRM-BLW算法的执行结果与最基本的naïve算法执行结果进行比较.为了便于比较,我们定义了DSMRM-BLW算法相对于其他算法的查全率与查准率.具体定义如下.设DSresult与Nresult分别为相同参数下DSMRM-BLW和naïve算法的执行结果集合,|DSresult|与|Nresult|分别是这2个集合中成员数目.令Vequal是这2个集合中相等的成员个数.这里定义DSresult中任一成员A与Nresult中成员B,如果它们对应的窗口起始位置相同,且A与B也相同,则A,B相等;如果二者中有1项不同,则A,B不相等.基于这些我们定义了DSMRM-BLW相对于naïve算法的查全率(recall)与查准率(precision),分别用Rrecall与Rprecision表示.使用它们来评价DSMRM-BLW算法的有效性. Rrecall=Vequal|Nresult|, (3) Rprecision=Vequal|DSresult|. (4) 表4给出了mushroom与retail样本下DSMRM-BLW算法分别相对于NI与NP算法的查全率与查准率.表4中我们用Rrecall,NI和Rprecision,NI分别表示DSMRM-BLW算法相对于NI算法的查全率与查准率,而用Rrecall,NP和Rprecision,NP分别表示DSMRM-BLW算法相对于NP算法的查全率与查准率. Table 4 Parameters and Results in Experiment 2 由表4可见,在不同数据样本及参数设置下,DSMRM-BLW算法相对于naïve算法的Rrecall与Rprecision的取值都为1,也即DSMRM-BLW算法与naïve算法的执行结果相同,即DSMRM-BLW算法能正确地得到界标窗口下数据流的最大规范模式. 4.4 DSMRM-BLW算法的性能评价 本节对DSMRM-BLW算法的时间与空间性能作了评测.因为目前并没有关于这方面的研究,所以使用的对比算法为前面提到的2类naïve算法.具体来说,我们在4.4.1节讨论了不同|EW|,λ以及样本大小Lsample与算法执行时间间的关系;而在4.4.2节讨论了不同|EW|,λ以及样本大小Lsample与算法空间开销间的关系. 4.4.1 DSMRM-BLW算法的时间开销分析 首先分析不同λ大小与算法执行时间之间的关系.实验效果如图4所示. 由图4可见,2类样本下DSMRM-BLW算法执行时间远小于其他2类算法.这说明边界界标窗口技术是有效的.另外还可以看到,2类样本下3种算法执行时间都随λ大小的增加而增加.这是因为λ越大,每个界标窗口中满足规范度小于λ条件的成员就越多.也即在同一窗口中,λ变大后满足规范度小于λ的成员个数大于等于λ变大前满足规范度小于λ的成员个数.对于NI算法,满足规范度小于λ的成员个数越多,算法需要处理的成员就越多,得到的规范模式数目也会增加.而因为我们需要消除所有规范模式间存在的超集关系,所以这时需要执行该操作的成员数目变得更多,算法时间会增加.同理对于NP算法,当满足规范度小于λ的成员个数增加时,算法中也增加了基于bit-sequence执行逻辑与操作的成员个数,得到的规范模式数目也会增加,而对于所有这些规范模式,NP算法也会通过消除它们间存在的超集关系来得到最大规范模式集合,所以算法时间会增加;DSMRM-BLW算法在第1个窗口上的情况与NP算法一样,之后每个窗口上会使用边界界标窗口技术来处理,所以算法时间开销主要决定于第1个窗口.由前面分析可知,该窗口上算法时间会随着满足规范度小于λ的成员个数增加而增加.另外当λ取值的增加并没有使窗口中满足规范度小于λ的项成员个数增加时,算法在这些窗口上的执行情况在λ取值改变前后变化不大(如图4(a)中的λ分别在40~60,80~100中取值);当λ取值的增加使窗口中满足规范度小于λ的项成员个数增加时,算法在这些窗口上执行时间会增加. 其次分析不同|EW|大小与算法执行时间之间的关系.实验效果如图5所示. Fig. 4 The comparison of the execution time about different algorithms when λ changes图4 算法在λ变化时的执行时间比较 Fig. 5 The comparison of the execution time about different algorithms when |EW| changes图5 算法在|EW|变化时的执行时间比较 由图5可见,2类样本下DSMRM-BLW算法执行时间小于其他2类算法,这说明边界界标窗口技术是有效的.另外可以看到NI与NP算法时间都随|EW|的增加而减少,这是因为对于同一个数据流来说,|EW|越大,算法在该数据流上执行最大规范模式挖掘的次数就越少,而且对于数据流上起始位置不变、终止位置以|EW|为单位不断滑动的界标窗口来说,当|EW|小时,naïve算法在数据流上执行挖掘的总次数以及所处理数据流成员的总量,大于|EW|变大后算法所执行挖掘的总次数以及所处理的数据流成员的总量,所以它们的时间都随窗口大小的增加而减少.DSMRM-BLW算法在第1个窗口上与NP算法一样,之后每个窗口上会使用边界界标窗口技术来处理,所以算法时间开销主要决定于第1个窗口.因为当|EW|变大时,变化后第1个窗口上的规范项数目小于等于变化前该窗口上的规范模式数目,所以对于稠密样本下第1个窗口上的DSMRM-BLW算法来说,当该窗口上规范模式数目不变时,因为窗口大小的增加会使该窗口上参与运算的bit-sequene规模变大,所以执行时间会增加(图5(a)中|EW|大小在100~500,700~900);当该窗口上的规范模式数目减少时,特别是当窗口大小的增加使得原第1个窗口上本来规范的项变得不规范时,界于样本自身的稠密特征,该算法在新窗口上的规范模式集合与原窗口上的规范模式集合相比,会少了很多与被删除项有关的规范模式,这样后期再执行消除规范模式集合中成员间超集关系的操作,时间开销会少很多,所以此时算法时间开销会减少(图5(a)中|EW|大小在500~700).对于稀疏样本下第1个窗口上的DSMRM-BLW算法,样本稀疏的特点会使得该窗口上的规范模式不多,同时数据结构的规模会很大,所以该窗口上的时间开销更多的是在于挖掘规范模式本身所花费的时间,消除所有规范模式间超集关系所花费的时间反而不多.当|EW|增加时,因为第1个窗口上数据结构的规模会变大,所以执行时间会增加.另外我们可以看到3种算法彼此间的时间差异会随|EW|的减少而增加,这是因为|EW|越小,算法执行挖掘的窗口及次数就越多,每个窗口上这3类算法执行时间都会有差异,随着窗口数目的增加,这种差异的累积就会越来越大,所以它们间执行时间的差别也会越来越大. 最后分析样本大小Lsample与算法执行时间之间的关系.实验效果如图6所示: Fig. 6 The comparison of the execution time about different algorithms when Lsample changes图6 算法在Lsample变化时的执行时间比较 由图6可见,2类样本下DSMRM-BLW算法执行时间小于其他2类算法,这说明边界界标窗口技术是有效的.另外可以看到这3类算法时间都随样本大小的增加而增加,这是因为对于同一个数据流来说,样本越大,算法在该样本上需要处理的数据流成员就越多,所以执行时间会随着样本大小的增加而增加;另外由图6中还可以看到,3类算法彼此间的时间差异会随着样本大小的增加而增加.这是因为样本越大,算法执行挖掘的窗口及次数就越多,每个窗口上这3类算法执行时间都会有差异,随着窗口数目的增加,这种差异的累积就会越来越大,所以它们间执行时间的差别也会越来越大. 4.4.2 DSMRM-BLW算法的空间开销分析 1) 分析不同λ大小与算法空间开销之间的关系.实验效果如图7所示. Fig. 7 The comparison of the space consumption about different algorithms when λ changes图7 算法在λ变化时的空间开销比较 由图7可以看到,在空间开销上DSMRM-BLW Fig. 8 The comparison of the space consumption about different algorithms when |EW| changes图8 算法在|EW|变化时的空间开销比较 另外从图7可以看到,3种算法空间开销随λ大小增加而单调增加.对于稠密样本下的NI与NP算法,样本的稠密性会使算法的空间开销决定于每个窗口上所有规范模式的规模.而当λ增加时,每个窗口中满足规范度小于λ的项成员数目可能会有2种变化:①数量保持不变;②数量增加.NI算法需要保留每个窗口上完整的规范模式集合,同时还需要开辟空间用于在该集合基础上得到最大规范模式集合,所以如果λ的增加没有使窗口中满足规范条件的成员数目发生变化,则NI算法用于存放规范模式集合的空间保持不变(如图7(a)中λ取值在40~60和80~100区间);如果λ的增加使得窗口中满足规范条件的成员数目增加,则NI算法用于存放规范模式的空间就会增加.对于NP算法,因为NP算法需要对每个窗口上所有项构建bit-sequence序列,另外NP算法也要开辟空间基于每个窗口上的完整规范模式集合来得到最大规范模式集合,所以NP算法与NI算法一样,空间开销都会随着λ取值的增加而单调递增.DSMRM-BLW算法在第1个窗口上执行情况与NP算法一样,所以该窗口上空间开销会随着λ的增加而单调递增.又因为该算法在其他窗口上使用边界界标窗口技术,所以空间开销并不大,也即此时整个算法的空间开销集中在第1个窗口上,于是空间开销会增加.总体来看,DSMRM-BLW算法在每个窗口上的空间开销会随着λ取值的增加而单调递增.对于稀疏样本下的算法,样本的稀疏性会使得每个窗口上规范模式的数目较少,且数据结构规模较大.这种情况下算法的空间开销决定于每个窗口上数据结构的规模.又因为3类算法在每个窗口上的数据结构与λ无关,所以可以看到它们在每个窗口上的空间开销基本相同. 2) 分析不同|EW|大小与算法空间开销间的关系.实验效果如图8所示. 由图8可以看到,DSMRM-BLW算法具有最好的空间开销,而且不同算法间空间开销的关系与λ变化时所呈现的状态一样.具体原因与在λ变化时不同算法空间开销间关系分析中己有说明,篇幅原因,这里不再赘述.稠密样本下2种naïve算法在每个窗口上的空间开销,都随|EW|增加而减小.这是因为对于界标窗口而言,当λ确定时,基本窗口较大情况下界标窗口中规范模式数目会小于等于基本窗口较小情况下界标窗口中的规范模式数目,所以用于存放小基本窗口下界标窗口中所有规范模式的空间开销大于等于大基本窗口下界标窗口中用于存放所有规范模式的空间开销.对于DSMRM-BLW算法,因为mushroom样本稠密性的特点,该算法在第1个窗口上的空间开销远远大于其他窗口上的空间开销,这时该算法的空间开销主要决定于这个窗口,当|EW|增加时,需要处理的界标窗口数会变小,这样平均每个窗口上的空间开销就会增加;retail样本下算法的空间开销都随|EW|增加而单调增加.这是因为样本稀疏的特点会使得每个界标窗口上满足规范条件的项变得很少,而且同时又会使窗口上的数据结构规模增加,所以这种情况下算法空间开销决定于每个窗口的数据结构规模.对于NI算法,因为窗口越大,其中成员越多,每个窗口上的前缀树规模就越大,所以空间开销会增加;对于NP算法与DSMRM-BLW算法,因为窗口越大,每个窗口上BVtable规模就越大,所以空间开销单调增加. 3) 分析样本大小Lsample与算法空间开销之间的关系.实验效果如图9所示: Fig. 9 The comparison of the space consumption on different algorithms when Lsample changes图9 算法在Lsample变化时的空间开销比较 由图9可见,DSMRM-BLW算法具有最好的空间开销;另外还可以看到稠密样本下3种算法空间开销都随样本大小增加而单调递减.对于2类naïve算法,因为随着样本大小的增加,会出现更多需要处理的界标窗口,而且这些窗口大小会越来越大,窗口上规范模式的数目会小于等于之前出现的窗口上规范模式的数目,所以平均每个窗口上的空间开销会单调减少;对于DSMRM-BLW算法,因为该样本下的空间开销决定于第1个界标窗口,所以随着窗口数目的增加,平均每个窗口的空间开销会越来越小.另外还可以看到稀疏样本下算法的空间开销都会随着样本大小的增加而单调增加.这是因为这类样本下算法的空间开销主要决定于每个窗口上的数据结构规模.对于NI算法,因为每个新增加窗口上的前缀树规模大于等于相邻前一个窗口上的前缀树规模,所以在样本大小增加过程中,每个窗口上平均空间开销会增加;对于NP算法,因为每个新增加窗口上的BVtable规模会大于相邻前一个窗口上的BVtable规模,所以在样本大小增加过程中,每个窗口上的平均空间开销也会增加;同理DSMRM-BLW算法在样本大小增加过程中,每个窗口上平均空间开销也会增加. 总之,由本节实验可以看到:①在需要定性确定数据集上哪些成员是规范模式时,挖掘最大规范模式有更好的效率,能在不减少规范模式所蕴含信息的同时,极大减少需要挖掘的模式数量;②DSMRM-BLW算法在挖掘界标窗口下数据流最大规范模式时,与naïve算法执行结果相同;③同2类naïve算法相比,DSMRM-BLW算法具有更好的时间与空间效率. 本文首次对于界标窗口下数据流最大规范模式挖掘问题进行了研究.首先给出了该问题的形式化描述;接着对处理该问题的naïve算法中相邻窗口上最大规范模式间的关系进行了分析,得到了边界界标窗口技术,并由此提出了DSMRM-BLW算法,与naïve算法相比,该算法在保持查询结果不变的同时,很好地减少了时间与空间开销;最后通过对于公有数据样本的实验证明了该算法的有效性.因为规范模式与频繁模式二者都具有向下闭包的特点,所以很多与数据流最大频繁模式挖掘相关的技术应该可以直接或间接地应用于数据流最大规范模式的挖掘中,所以未来研究中我们会着重分析这二者间的关系,争取进一步提高DSMRM-BLW算法的执行效率;另外,界标窗口中历史数据的重要性会随着时间的推移而减小.为了能够体现出这个特点,可以将衰减模型与DSMRM-BLW算法相结合,这也是未来应该着手做的一个研究方向. [1]Tanbeer S K, Ahmed C F, Jeong B S. Mining regular patterns in data streams[C]Proc of the 15th Int Conf on Data Systems for Advanced Applications. Berlin: Springer, 2010: 399-413 [2]Li Guohui, Chen Hui. Mining the frequent patterns in an arbitrary sliding window over online data stream[J]. Journal of Software, 2008, 19(10): 2585-2596 (in Chinese)(李国徽, 陈辉. 挖掘数据流任意滑动窗口内频繁模式[J]. 软件学报, 2008, 19(10): 2585-2596) [3]Yun U, Lee G, Ryu K H. Mining maximal frequent patterns by considering weight conditions over data streams[J]. Knowledge-Based Systems, 2014, 55: 49-65 [4]Lee G, Yun U, Ryu K H. Sliding window based weighted maximal frequent pattern mining over data streams[J]. Expert Systems with Applications, 2014, 41(2): 694-708 [5]Hang Meng, Wang Zhihai, Yuan Jidong. Efficient method for mining closed frequent patterns from data streams based on time decay model[J]. Chinese Journal of Computers, 2015, 38(7): 1473-1483 (in Chinese)(韩萌, 王志海, 原继东. 一种基于时间衰减模型的数据流闭合模式挖掘方法[J]. 计算机学报, 2015, 38(7): 1473-1483) [6]Tanbeer S K, Ahmed C F, Jeong B S. Mining regular patterns in incremental transactional databases[C]Proc of the 12th Asia-Pacific Web Conf. Piscataway, NJ: IEEE, 2010: 375-377 [7]Kumar G V, Sreedevi M, Kumar N P. Mining regular patterns in data streams using vertical format[J]. International Journal of Computer Science and Security, 2012, 6(2): 142-149 [8]Verma V K, Saxena K. Mining regular pattern over dynamic data stream using bit stream sequence[J]. International Journal of Innovative Technology and Exploring Engineering, 2013, 3(7): 7-10 [9]Kumar G V, Kumari V V. Sliding window technique to mine regular frequent patterns in data streams using vertical format[C]Proc of the Int Conf on Computational Intelligence and Computing Research. Piscataway, NJ: IEEE, 2012: 1-4 [10]Sreedevi M, Reddy L S S. Mining closed regular patterns in data streams[J]. International Journal of Computer Science & Information Technology, 2013, 5(1): 171-179 [11]Rashid M M, Karim M R, Jeong B S, et al. Efficient mining regularly frequent patterns in transactional databases[C]Proc of the 17th Int Conf on Database Systems for Advanced Applications. Berlin: Springer, 2012: 258-271 [12]Rashid M M, Gondal I, Kamruzzaman J. Regularly frequent patterns mining from sensor data stream[C]Proc of the 20th Int Conf on Neural Information Processing. Berlin: Springer, 2013: 417-424 [13]Agrawal R, Srikant R. Fast algorithms for mining association rules in large database[C]Proc of the 20th Int Conf on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann, 1994: 1-32 Wen Yingyou, born in 1974. PhD and post doctor of Northeastern University. Member of CCF. His main research interests include next generation network, wireless sensor network, network security and network management (wenyy@neusoft.com). Wang Shaopeng, born in 1984. PhD from Northeastern University. Member of CCF. His main research interests include data stream and wireless sensor network. Zhao Hong, born in 1954. Professor and PhD supervisor of Northeastern University. Senior member of CCF. His main research interests include computer network security and information security, distributed multimedia, and network management (zhaoh@neusoft.com). The Maximal Regular Patterns Mining Algorithm Based on Landmark Windowover Data Stream Wen Yingyou1,3, Wang Shaopeng1,2, and Zhao Hong1,3 1(CollegeofComputerScienceandEngineering,NortheasternUniversity,Shenyang110819 )2(CollegeofComputerScience,InnerMongoliaUniversity,Huhhot010021)3(KeyLaboratoryofMedicalImageComputing(NortheasternUniversity),MinistryofEducation,Shenyang110819 ) Mining regular pattern is an emerging area. To the best of our knowledge, no method has been proposed to mine the maximal regular patterns about data stream. In this paper, the problem of mining maximal regular patterns based on the landmark window over data stream is focused at the first time. In order to resolve the issue that the naïve algorithm which is used to handle the maximal regular patterns mining based on the landmark window over data stream does not have the characteristic of incremental computation, the DSMRM-BLW(data stream maximal regular patterns mining based on boundary landmark window) algorithm is proposed. It takes the first window as the boundary landmark window, and handles it with the naïve algorithm. For all other windows, it can obtain the maximal regular patterns over them based on the ones over the adjacent last window incrementally, and can overcome the drawback of the naïve algorithm. It is revealed by the extensive experiments that the DSMRM-BLW algorithm is effective in dealing with the maximal regular patterns mining based on the landmark window over data stream, and outperforms the naïve algorithm in execution time and space consumption. data stream; landmark window; maximal regular pattern; incremental calculation; boundary landmark window technology 2015-09-06; 2016-02-16 国家自然科学基金项目(60903159,61173153,61402096,61163011,61262082,61662054);中央高校基本科研业务费专项资金项目(N110818001,N100218001,N130504007,N120104001);国家“八六三”高技术研究发展计划基金项目(2015AA016005);沈阳市科技计划项目(1091176 -1-00);内蒙古自然科学基金项目(2015MS0612) This work was supported by the National Natural Science Foundation of China (60903159, 61173153, 61402096, 61163011, 61262082, 61662054), the Fundamental Research Funds for the Central Universities (N110818001, N100218001, N130504007, N120104001), the National High Technology Research and Development Program of China (863 Program)(2015AA016005), the Science and Technology Plan of Shenyang of China (1091176-1-00), and the Natural Science Foundation of Inner Mongolia (2015MS0612). TP3113 基于边界界标窗口技术的数据流最大规范模式挖掘算法


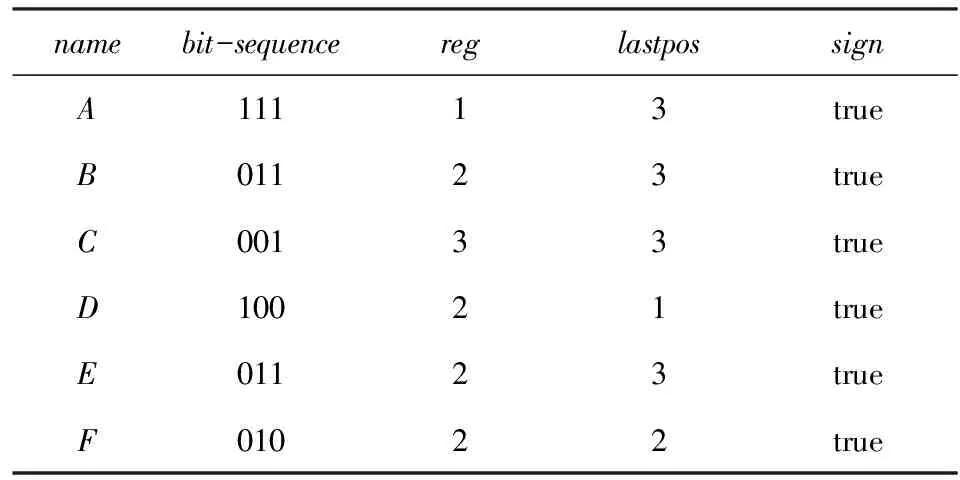


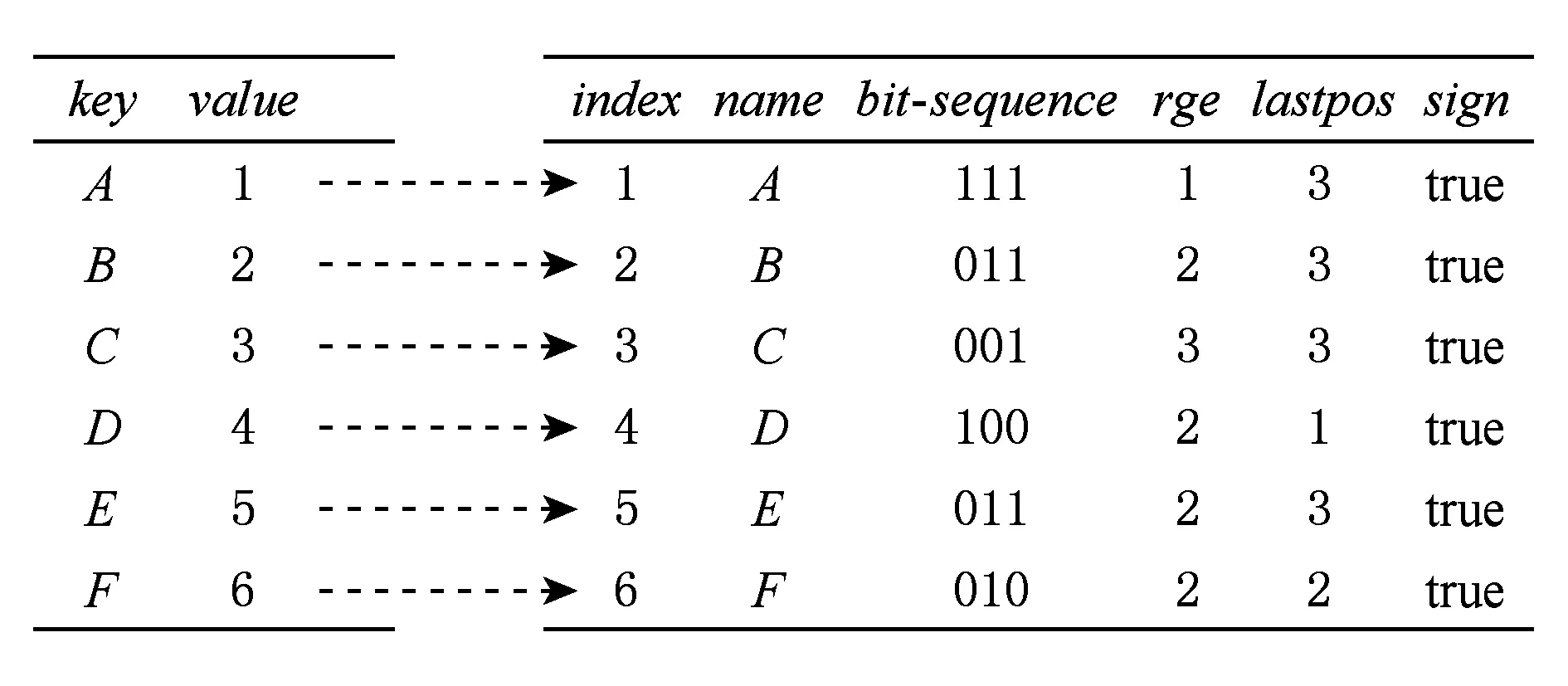
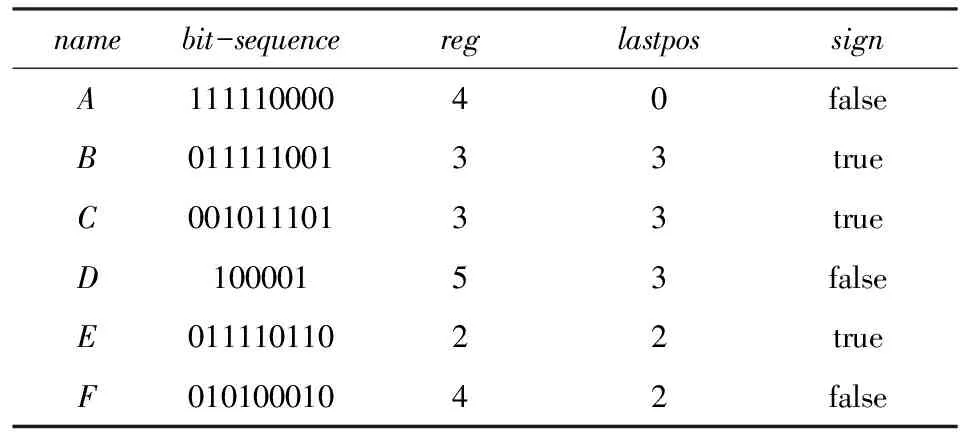

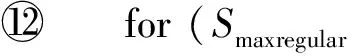










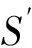
4 实验及结果分析



5 总结与展望



