一种支持变形基24 FFT的4路并行访存方法

杨 超 陈海燕 刘 胜

(国防科学技术大学计算机学院 长沙 410073)(yc.nudt@gmail.com)

一种支持变形基24FFT的4路并行访存方法

杨 超 陈海燕 刘 胜

(国防科学技术大学计算机学院 长沙 410073)(yc.nudt@gmail.com)

IEEE 802.15.3c是高速无线个人局域网(high-rate wireless personal area networks, WPANs)的国际统一标准，该标准要求采样频率为2.592 GHz的情况下在222.2 ns内完成512点FFT运算，这对FFT处理器提出了极高的标准.为了满足这一要求，部分FFT处理器采用了变形的基24FFT算法以及多运算单元(processing element, PE)并行的方法.在多PE并行的情况下，只有支持其无冲突并行访问操作数以及并行按序输入输出数据的存储系统设计，才能完全发挥出多个PE单元并行的优势.根据4路并行变形的基24FFT运算单元访问操作数的规律，设计了一种支持4路PE并行访问操作数的地址转换方法；并且该方法支持并行按序输入输出数据，这解决了由于数据输入或者输出需要进行位反序操作给并行按序输入输出带来的困难.最后基于同一综合约束条件进行逻辑综合，结果表明：该方法比之前的方法节约面积46%，功耗节约了28%，并且该方法支持连续数据流(continuous-flow)操作以及即位运算(in-place).

IEEE 802.15.3c标准；基24；FFT算法；地址转换；并行；即位运算；连续数据流

快速傅里叶变换(fast Fourier transform, FFT)算法在数字信号处理中得到了越来越广泛的应用，比如图像处理、媒体信号处理、光谱分析、电力系统、医学分析中等.近些年来，正交频谱分解技术 (orth-ogonal frequency-division multiplexing, OFDM)在无线通信领域中得到了越来越广泛的应用，而OFDM技术的基础是FFT算法；因此，随着无线通信系统需求的发展，FFT处理器的硬件加速性能变得越来越重要.

为满足无线通信应用需求的发展，IEEE订立了多种标准[1]，比如IEEE 802.11agn，IEEE 802.16e(OFDMA)，IEEE 802.16e(OFDM)标准等.FFT算法作为这些标准的核心和基础算法，其运算的实时性和处理速度要求越来越高.而802.15.3c标准，就是针对高速无线个人局域网(high-rate wireless personal area networks, WPANs)设计的标准，该标准针对采样频率为2.592 GHz的512点数据进行FFT运算，FFT处理器完成512点数据的处理时间小于222.2 ns，这对处理器的设计实现带来了极大的困难.

目前，各种各样的FFT处理器已经被设计出来，但是总体归纳起来主要分为2类：基于流水结构的FFT处理器[2-5]和基于存储结构的FFT处理器[6-7].基于流水线的处理器吞吐率和实时性比较高，但是这类处理器需要占用更多的面积和功耗；由于基于存储的FFT处理器具有占用面积和功耗小的优点，目前在嵌入式应用领域引起了越来越多的重视.

为了满足应用需求的不断增长，文献[8-9]中提出了针对特定领域更高效的FFT算法，文献[10]中的数字信号处理器为FFT算法设计了专用的指令集和体系结构，文献[4,9]中采用了多个运算单元(processing element, PE)并行的结构以提高运算性能.

在采用多个PE单元并行运算的结构下，存储接口是连接存储器与输入和输出(IO)设备以及运算单元之间的桥梁，只有存储系统支持多个操作数并行访问，避免访存冲突引起FFT处理数据停顿，才能发挥出FFT处理器并行运算单元最大的数据运算能力.并且在高速的FFT处理器中IO单元和并行运算单元的数据带宽应当匹配，这就要求数据IO单元能实现并行存取.然而由于在FFT运算的开始或者结束需要进行位反序操作，这就给输入或者输出的并行带来了困难.因此，一个支持运算过程中操作数并行访问，以及支持数据并行按序输入或输出的存储系统至关重要，这直接影响着处理器性能的发挥.然而文献[1,11-14]采用的按位相加、个别地址位异或等地址转换方法仅仅针对基24或者固定基r有效，并不支持多路变形的基24FFT PE单元并行访问操作数以及数据并行按序输入或者输出.

1 算法原理

1.1 传统基24算法

N个样本点的DFT为

(1)

k=0,1,…,N-1,

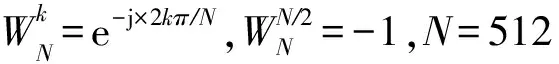
(2)

n1,k1=[0:15];n2,k2=[0:31].

将式(2)带入式(1)中:

X(16k2+k1)=

(3)

接下来可以继续对式(3)进行1级基24FFT运算，之后进行1级基2运算，即可完成运算.

通过式(3)我们可以发现，采用传统的基24FFT运算，一共需要24个存储体、1个基24与基2 FFT运算单元，然而基24运算单元复杂度比较高，并且采用这种传统的算法必须进行3级FFT运算.

指除职业暴露外其他个人行为发生的HIV暴露。暴露评估及处理原则尤其是阻断用药与职业暴露相似。尤其注意评估后阻断用药是自愿的原则及规范随访，以尽早发现感染者。

1.2 变形的基24算法

文献[9]提出了一种变形的基24FFT算法，可以将16个操作数继续分割成4个1组，采用4次基4 FFT算法以及简单的乘加单元即可完成.

n1=4m1+m2,

(4)

m1,m2,t1,t2=[0:3],

(5)

2 无冲突设计

2.1 需求分析

针对IEEE 802.15.3c设计标准，采样时钟频率是2.592 GHz，假设FFT处理器的时钟频率是采样频率的18，即2.592 GHz×18=0.324 GHz.在IEEE 802.15.3c标准里，在连续数据流的情况下，整个运算的时间只有222.2 ns，则在处理器运算和IO并行的情况下，处理器运算时间和IO时间只有72个时钟周期.为了达到这一要求，表1列出了采用各种不同的基所需要的运算级数、蝶形操作数总个数以及最大基的PE的并行度.

Table1 The Demand of FFT Processor of IEEE 802.15.3c

可以从表1中看出，基4 FFT算法为主的情况下一共需要4级基4和1级基2 FFT运算，最低需要16个基4 PE并行；基8 FFT算法为主下一共需要3级基8 FFT运算，最低需要4个基8 PE并行；基16 FFT算法为主的情况下，一共需要2级基16 和1级基2 FFT运算，基16 PE并行数最低为2.采用这些传统的FFT算法，在满足时间要求的前提下，由于并行度过高，需要消耗大量的面积.而采用上述变形的基24FFT算法，并且结合存储无冲突设计以及IO全并行的方法可以解决该问题.

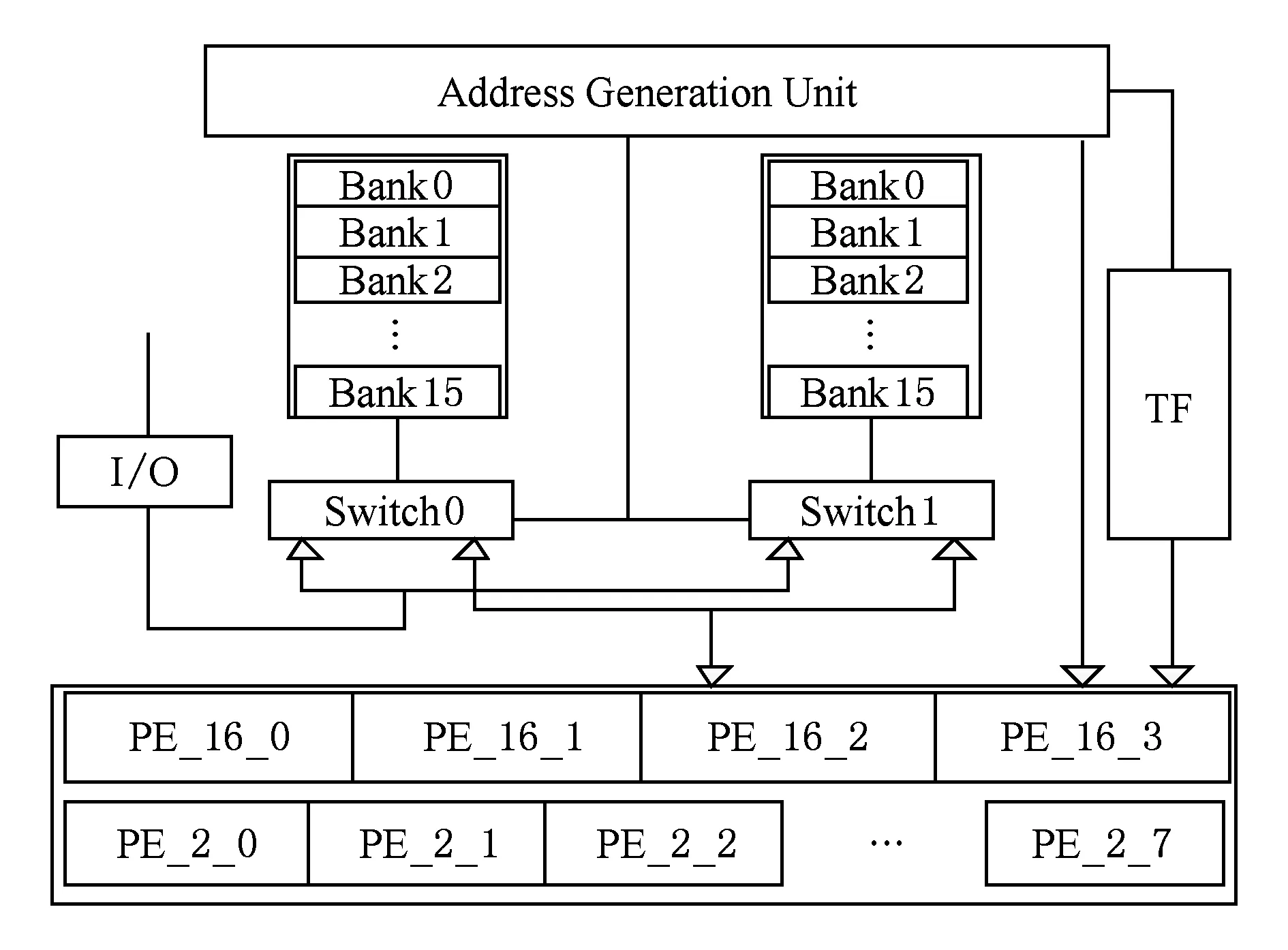
Fig. 1 The architecture of FFT processor图1 FFT处理器结构图

为了满足上述应用需求，采用16个存储体，并行进行4路变形的基24FFT算法，第1级操作顺序不做要求，第2级要求相邻的2路取数在运算完成后直接进行基2 FFT运算[9,15].虽然文献[16]里的设计也可以在第2级基16 FFT运算完成后，结果不用存回存储器而直接进行基2 FFT运算，但是文献[16]所采用的变形基16 FFT算法流水线过长，PE单元占用面积比较大.为了完成上述设计，支持4路运算单元同时运算，并且支持在第2级运算完成后可以不用存回而直接进行基2 FFT运算，存储器的并行访问设计是关键.该处理器结构如图1所示，图1中2个存储器均包含有16个双端口的存储体；该FFT处理器通过控制开关Switch0以及Switch1完成连续数据流操作；PE单元主要包括4个变形基16 PE和8个基2 PE.

2.2 操作数并行访问设计

本文主要针对操作数的并行访问进行优化，旋转因子可以采用文献[9,17]中提出的计算方法.在采用上述算法设计时，第1级变形的基24FFT算法4路运算单元同时取数的地址如表2所示:

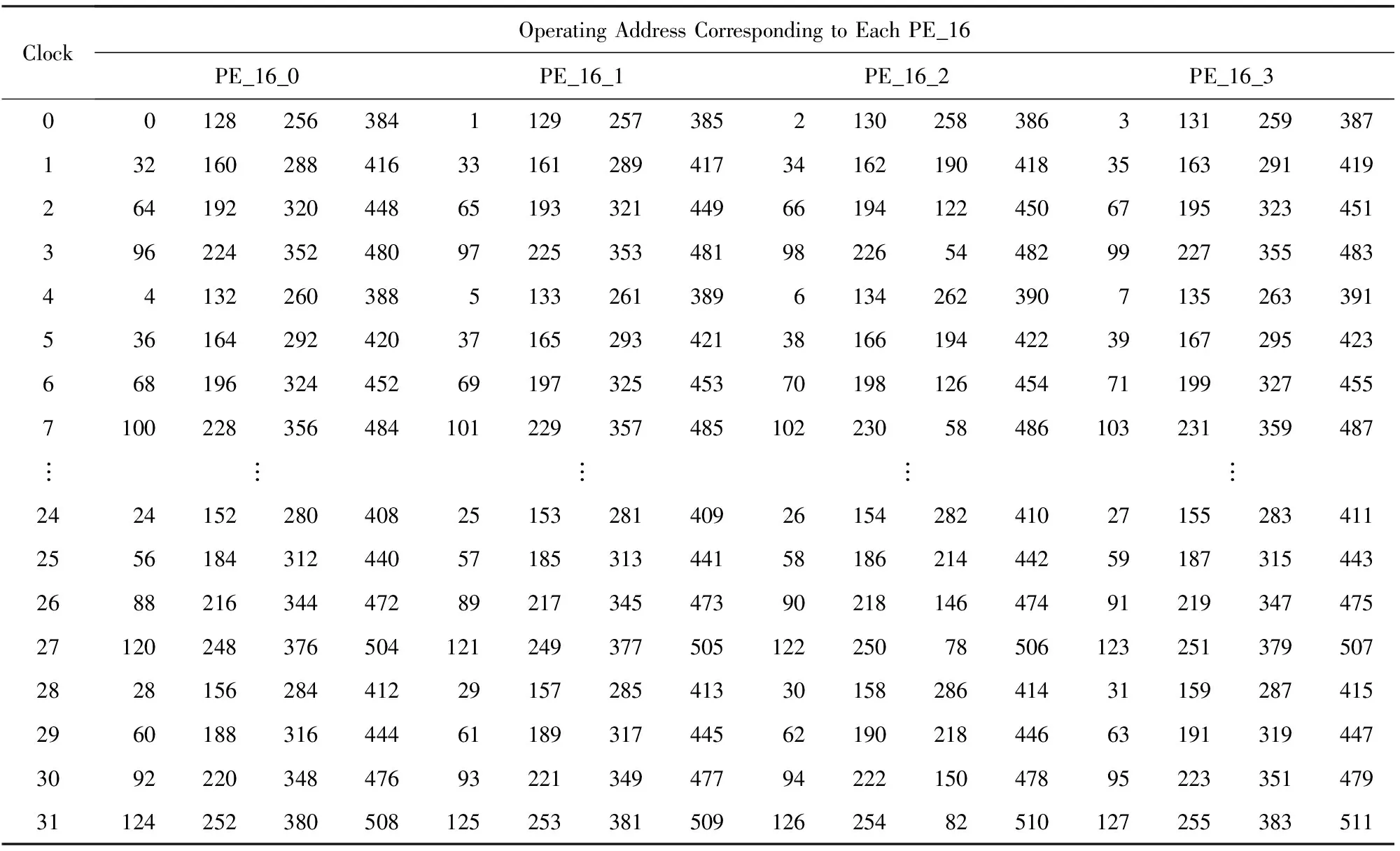
Table2 Operating Access Order in the First Stage

在FFT运算的第1级，同一个时钟周期需要取出的操作数可以表示为：k,k+128,k+256,k+384,k+1,k+129,k+257,k+385,k+2,k+130,k+258,k+386,k+3,k+131,k+259,k+387; 在每次基24运算的子基4运算时，k值加32；在每次基24运算结束时，下一个基24运算的k值相对于上一次基24运算的初始k值加上4.

第2级4路并行基24FFT运算，必须在相邻2路基24FFT运算完成后可以直接进行基2 FFT运算，数据的访问如表3所示.

在FFT运算的第2级，同一个时钟周期需要取出的操作数可以表示为：k,k+8,k+16,k+24,k+1,k+9,k+17,k+25,k+32,k+40,k+48,k+56,k+33,k+41,k+49,k+57.在每次基24运算的子基4运算时，k值加2；在每次基24运算完成时，下一个基24运算的初始k值相对于上一次基24运算的初始k值加64.

通过该运算访问操作数的顺序我们可以发现，在采用16体低位交叉的存储方式时，第1,2级每次需要取出的16个操作数分别存在于2个存储体里，需要8个节拍才能取出，而这8个节拍期间PE会处于闲置状态，故一般的低位交叉存储方式并不适合该种变形算法.只有4路基24FFT运算需要访问的16个操作数可以无冲突并行取出，才可以充分发挥运算单元的并行性，才能在第2级基24FFT运算完成后直接进行基2 FFT运算，以达到节约时钟周期的目的.

在上述2级运算中，每一个访存节拍只有对存储器准确高效地读写4路PE并行运算结构才能完全发挥出性能.而地址位b[8:7],b[2:0]可以区分出第1级的数据地址，地址位b[6:3],b[0]可以区分出第2级的数据地址.这里我们令addr表示地址所在的行，bank代表地址所在的存储体，本文中，bank和addr分别表示如式(6)所示：

(6)

在采用式(6)中地址转换方法转换后，地址排列如表4所示.从表4可看出，在地址访问的第1级和第2级，1次16个操作数可以并行无冲突取出，这就说明该地址转换可以有效支持变形的基24FFT算法4路同时操作，在第2级运算完成后可以直接进行基2 运算，节省了时钟数.

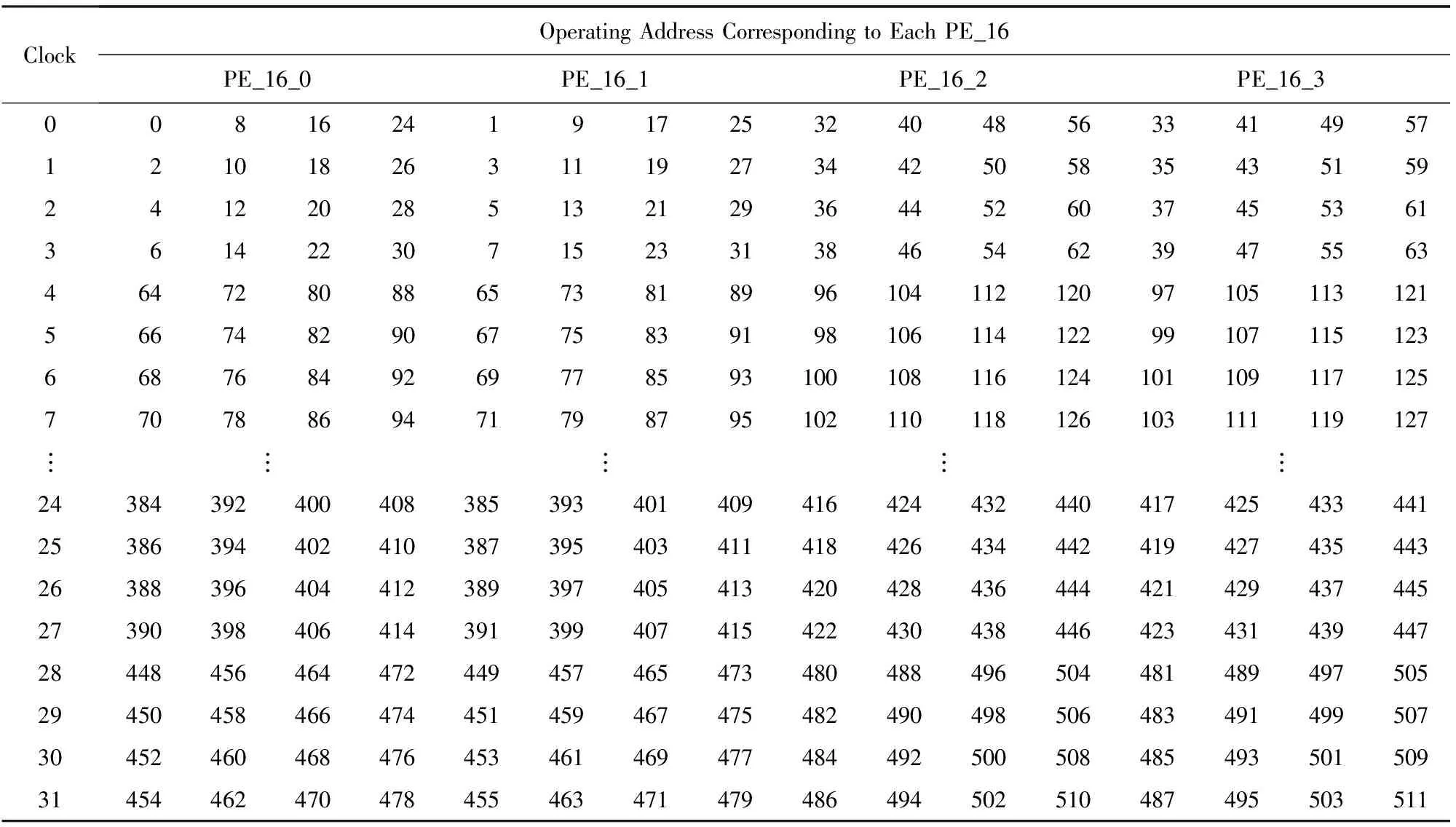
Table 3 Operating Order in the Second Stage

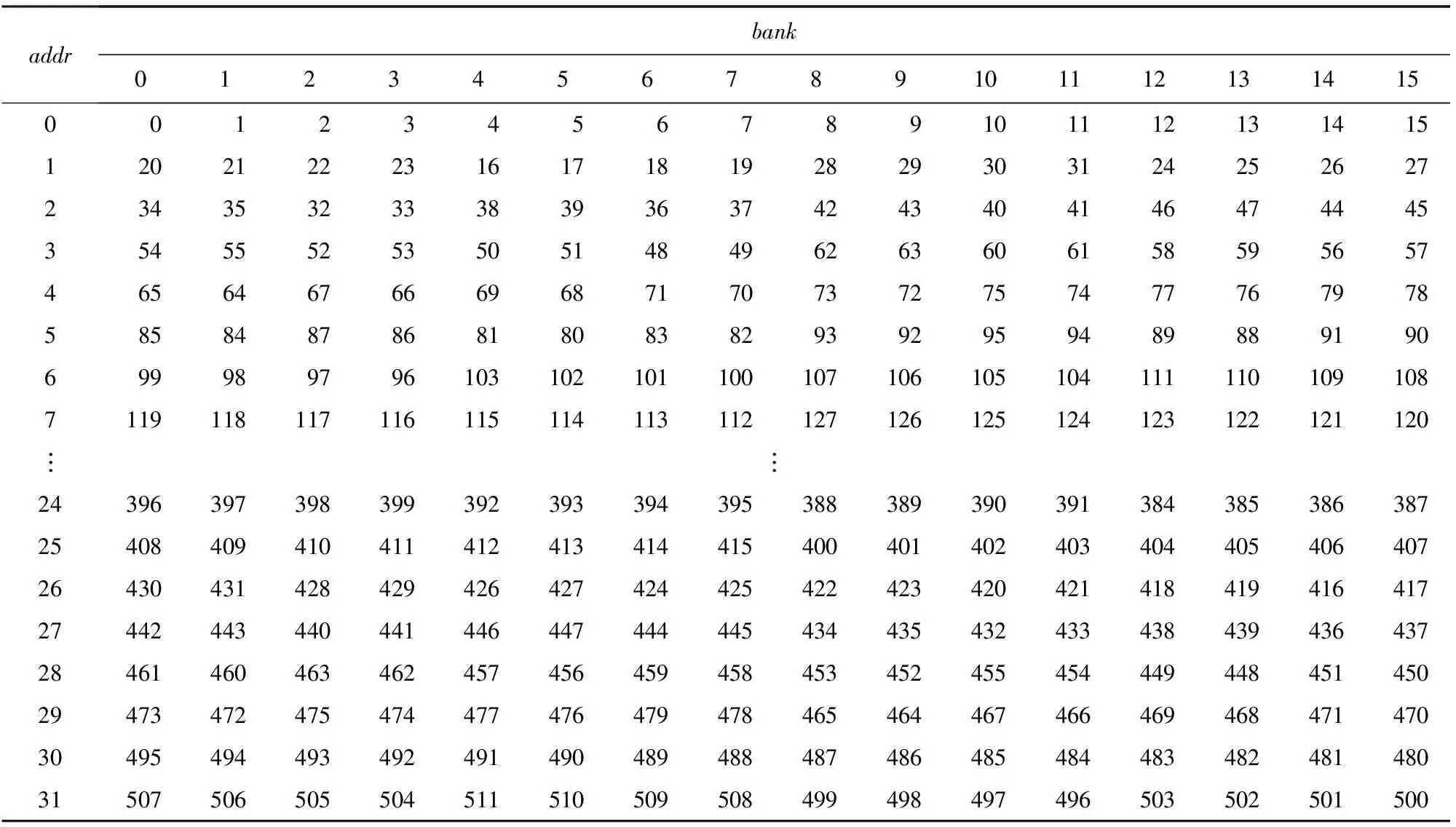
Table 4 Address Scheme After Transformation

2.3 结果并行顺序输出

为了在规定的时钟周期内完成运算，数据的并行输入和输出至关重要.假设采用频域分解DIF方法，数据的输入可以并行顺序输入，然而结果输出时，由于需要进行位反序(bit reversal)操作，这给结果的并行按序输出带来了难度.所以衡量一个地址转换方法的好坏，除了是否支持操作数可以并行访问，运算结果可以并行顺序输出也是关键.而本文中的地址转换方法可以支持运算结果并行顺序输出.

在运算结果输出时，运算结果是X(k)，地址k=k[8:0].数据输入为x(n)，n可以表示为b[8:0].则k用n表示为k=k[8:0]={b[0],b[4:1],b[8:5]}.每个时钟周期，并行输出X(16m)～X(16m+15),m=[0:31].m初始值为0，每过一个时钟周期，m值增加1，即运算结果地址位k[8:4]每次增加1，一直增加到m值为31，即完成一次完整的运算结果输出.表5给出了运算结果顺序输出分别对应的bank地址和addr地址.

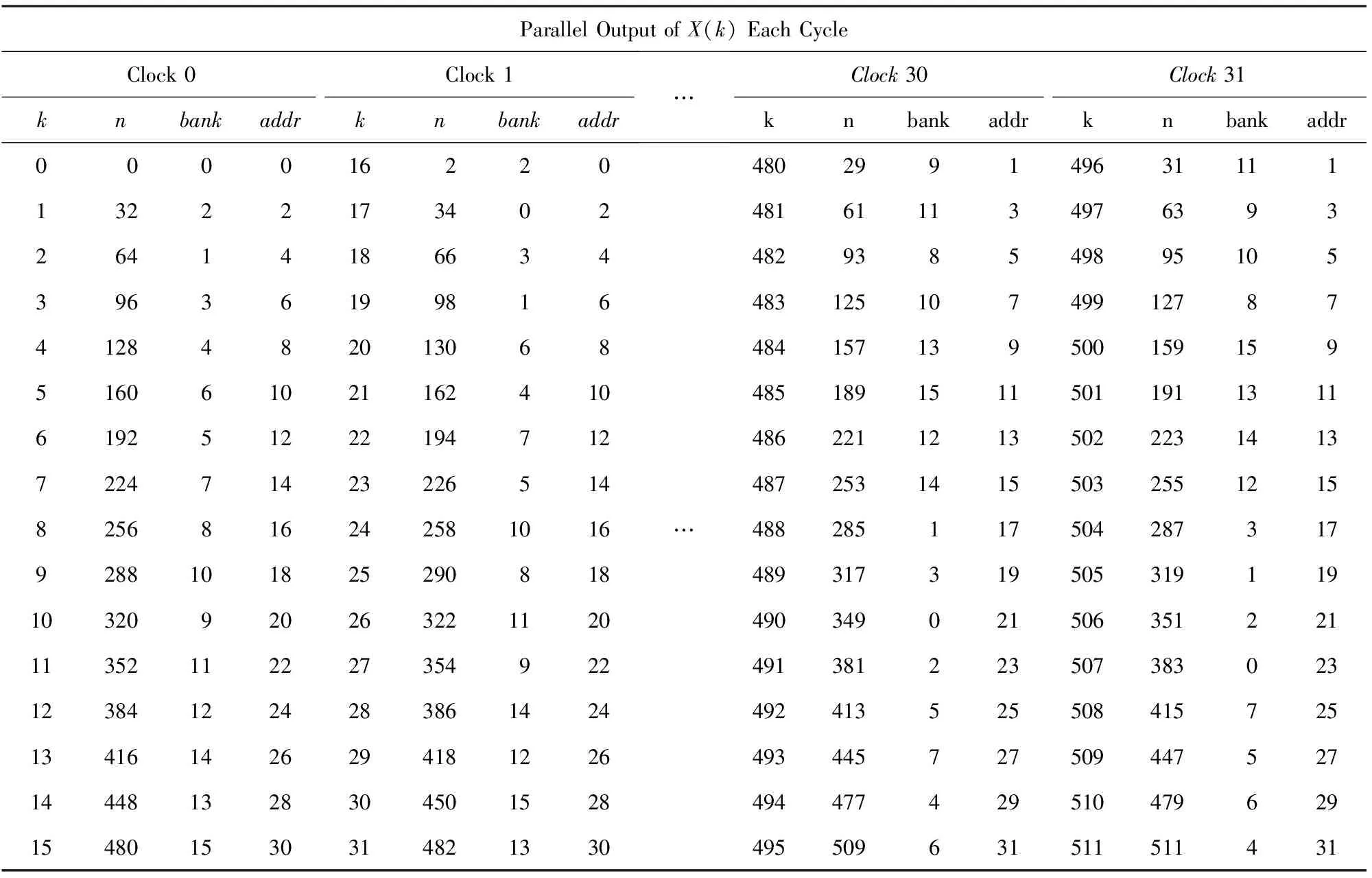
Table 5 Parallel and Normal Order Output of Result

从表5可以看出，在每一个时钟周期并行输出的16个连续的运算结果，均存放在不同的bank体内，也即本文中提出的地址转换方法支持运算结果并行按序输出.

3 实现与对比

在文献[1,11-14]中提出的FFT处理器无冲突并行地址排列方法，要么不支持多路变形的基24PE并行访问操作数，要么不支持数据并行按序输入或者输出.在文献[9,15]中，为了支持4路变形的基24FFT运算单元并行访问操作数且数据并行按序输入或者输出的地址转换式为

(7)

对比式(6)(7)，可以看出式(7)中采用的地址转换方法，除了需要进行异或操作外，还要对2个2位二进制地址进行乘法操作以及对2进制地址进行1次模4和模16操作.而本文中的地址转换方法，可以仅仅通过3个2输入异或门和1个3输入异或门进行实现，地址转换电路实现非常简单.将式(6)中的地址转换方法，用电路进行实现，b[8:0]代表初始地址，a[8:0]代表转换后的完整地址，如图2所示：

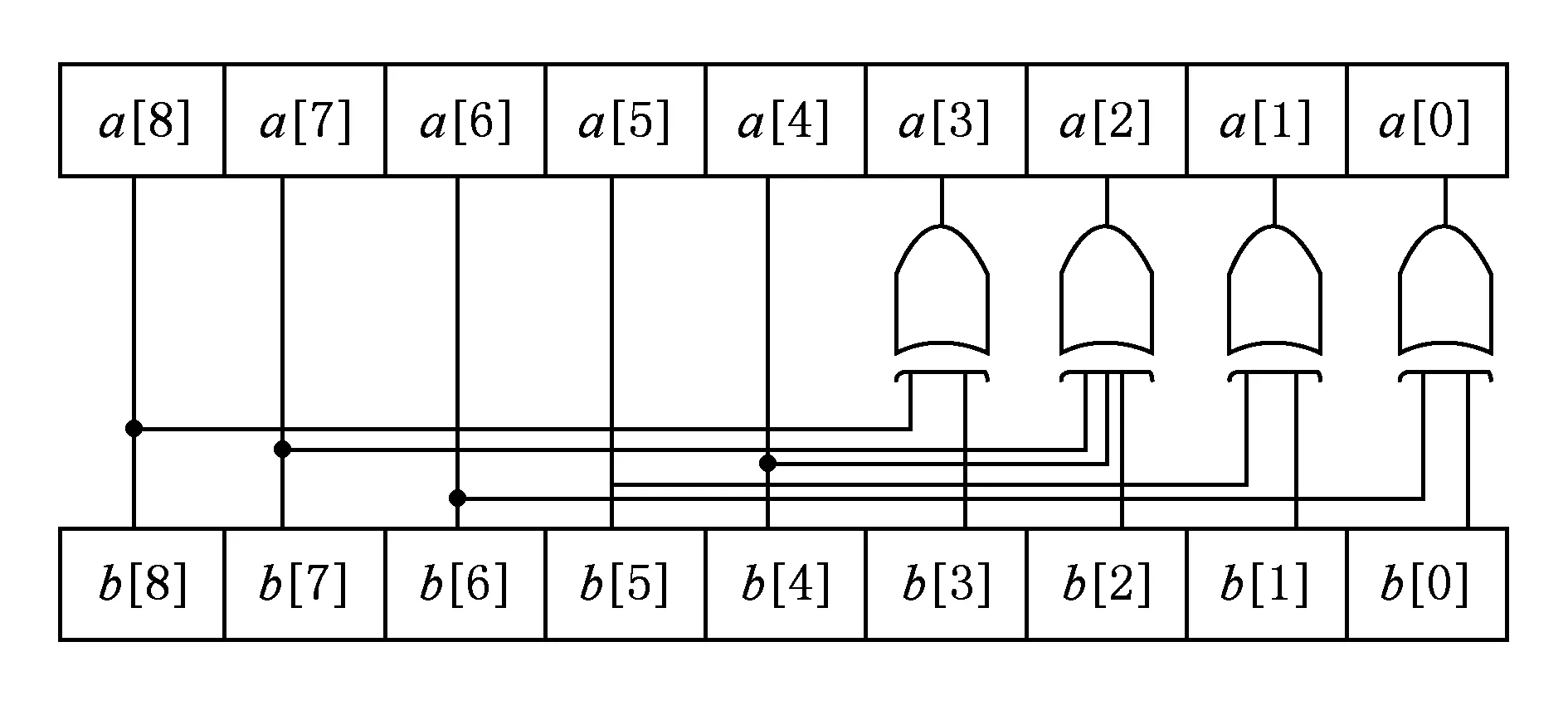
Fig. 2 Circuit of address transformation图2 地址转换电路

图1中地址生成单元主要包括操作数地址生成单元[9]和输出结果地址生成单元(DIF情况下，原始数据并行按序输入很简单，所以不做介绍)，分别如图3、图4所示.图3和图4中的Address Trans-formation Unit就是地址转换单元.图3中，计数器从0开始，每个周期加1，一直到31即完成1级FFT运算，2级运算都完成后，整个512点FFT运算结束.图4中，计数器从0每次加1到31，即可完成512点数据并行按序输出，图4中显示地址为k值位反序后的n值，结果输出顺序和表5一样.

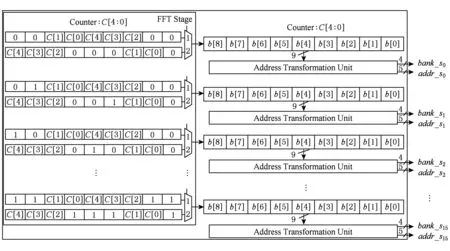
Fig. 3 Circuit of operating address generation图3 操作数地址生成单元

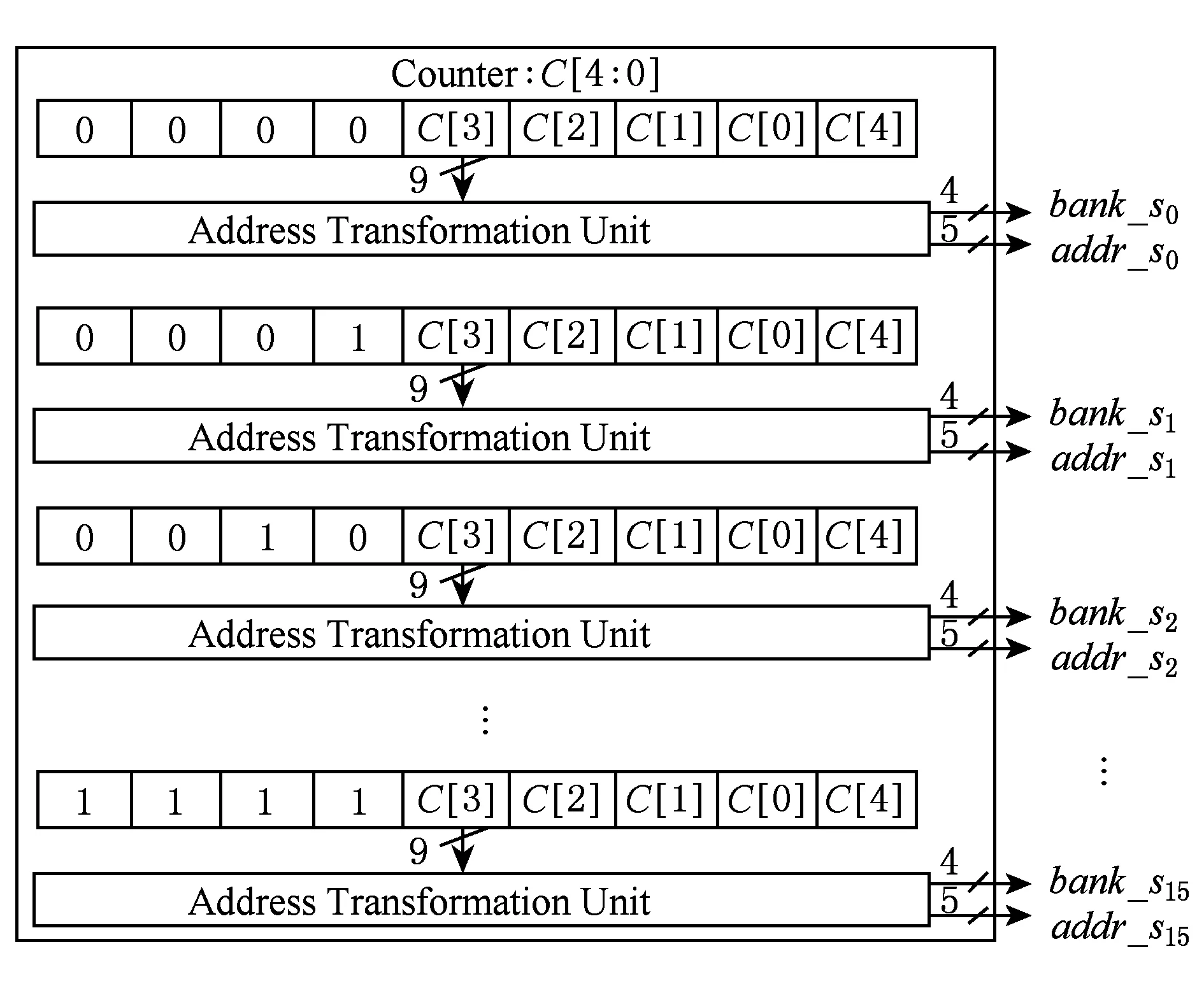
Fig. 4 Circuit of output result address generation图4 输出结果地址生成单元

将本文中提出的方法与文献[9,15]中采用的方法也即式(7)，在某厂家65 nm工艺下进行综合，结果显示式(7)综合的面积为81 nm2，功耗为110μW；而本文中的面积约为44 nm2，功耗为79μW；而且在连续数据流的2组双端口存储器里，如图3和图4所示，数据输入输出以及运算取操作数和存中间运算结果共需要2组地址转换单元，故一共需要16×2=32个地址转换单元，故本文中的地址转换方法相对文献[9,15]中采用的方法一共节约面积(81-44)×32 nm2=1 184 nm2，功耗节约了(110-79)×32μW=992 μW.最后经过对比，本文中的方法比式(7)的方法节约面积46%，功耗节约了28%.

4 总 结

本文提出了一种极其简单的支持4路变形基24FFT算法并行访问操作数的地址转换方法，它支持即位运算和连续数据流；更重要的是，这种简单的地址转换方法同时可以支持在位反序的情况下数据并行按序输入或者输出，这就可以减少后续其他部件等待FFT运算结果的时间.本文中的方法相对之前方法的实现更为简单，最后的面积和功耗的综合结果表明了本文中的地址转换方法是最优的.

[1]Tsai P Y, Lin C Y. A generalized conflict-free memory addressing scheme for continuous-flow parallel-processing FFT processors with rescheduling[J]. IEEE Trans on Very Large Scale Integration Systems, 2012, 19(12): 2290-2302

[2]Chang Yunnan, Parhi K. An efficient pipelined FFT architecture[J]. IEEE Trans on Circuits and Systems II: Analog and Digital Signal Porcessing, 2003, 50(6): 322-325

[3]Lin Yuwei, Liu Hsuanyu, Lee Chenyi. A 1-GSs FFTIFFT processor for UWB applications[J]. IEEE Journal of Solid-State Circuits, 2005, 40(8): 1726-1735

[4]Shin M, Lee H. A high-speed four-parallel radix-24FFTIFFT processor for UWB applications[C]Proc of IEEE ISCSA’08. Piscataway, NJ: IEEE, 2008: 960-963

[5]Cho T, Lee H, Park J, et al. A high-speed low-complexity modified radix-25 FFT processor for gigabit WPAN applications[C]Proc of IEEE ISCAS’11. Piscataway, NJ: IEEE, 2011: 1259-1262

[6]Ma Y, Wanhammar L. A hardware efficient control of memory addressing for high-performance FFT processors[J]. IEEE Trans on Signal Processing, 2000, 48(3): 917-921

[7]Baas B M. A low-power, high-performance, 1024-point FFT processor[J]. IEEE Journal of Solid-State Circuits, 1999, 34(3): 380-387

[8]Fang Wei, Sun Guangzhong, Wu Chao, et al. A parallel algorithm of three-dimensional fast Fourier transform[J]. Journal of Computer Research and Development, 2011, 48(3): 440-446 (in Chinese)(方维, 孙广中, 吴超, 等. 一种三维快速傅里叶变换并行算法[J]. 计算机研究与发展, 2011, 48(3): 440-446)

[9]Huang S J, Chen S G. A high-throughput radix-16 FFT processor with parallel and normal inputoutput ordering for IEEE 802.15.3c systems[J]. IEEE Trans on Circuits and Systems I: Regular Papers, 2012, 59(8): 1752-1765

[10]Chen Shuming, Li Zhentao, Wan Jianghua, et al. Research and development of high performance YHFT digital signal processor [J]. Journal of Computer Research and Development, 2006, 43(6): 993-1000 (in Chinese)(陈书明, 李振涛, 万江华, 等. 银河飞腾"高性能数字信号处理器研究进展[J]. 计算机研究与发展, 2006, 43(6): 993-1000)

[11]Sorokin H, Takala J. Conflict-free parallel access scheme for mixed-radix FFT supporting IO permutations[C]Proc of IEEE ICASSP’11. Piscataway, NJ: IEEE, 2011: 1709-1712

[12]Takala J H, Jarvinen T S, Sorokin H T. Conflict-free parallel memory access scheme for FFT processors[C]Proc of IEEE ISCAS’03. Piscataway, NJ: IEEE, 2003: IV-524-IV-527

[13]Reisis D, Vlassopoulos N. Conflict-free parallel memory accessing techniques for FFT architectures[J]. IEEE Trans on Circuits and Systems I: Regular Papers, 2008, 55(11): 3438-3447

[14]Richardson S, Markovic D, Danowitz A, et al. Building conflict-free FFT schedules[J]. IEEE Trans on Circuits and Systems I: Regular Papers, 2015, 62(4): 1146-1155

[15]Liu Weichang, Wei Tingchen, Huang Yashiue, et al. All-digital synchronization for SCOFDM mode of IEEE 802.15.3c and IEEE 802.11ad[J]. IEEE Trans on Circuits and Systems I: Regular Papers, 2015, 62(2): 545-553

[16]Huang Shenjui, Chen Saugee. A green FFT processor with 2.5-GSs for IEEE 802.15.3c (WPANs)[C]Proc of IEEE ICGCS’10. Piscataway, NJ: IEEE, 2010: 9-13

[17]Huang S J, Chen S G. A new memoryless and low-latency FFT rotator architecture[C]Proc of ISIC’14. Piscataway, NJ: IEEE, 2014: 180-183

Yang Chao, born in 1990. Received his MSc degree from the College of Computer, National University of Defense Technology (NUDT), China, in 2015. PhD candidate in the College of Computer, NUDT, China. His main research interests include FFT processor, memory system and SIMD.

Chen Haiyan, born in 1967. Received her BE and master degrees in computer science from NUDT, China. Currently a professor in the College of Computer, NUDT, China. Her main research interests include VLSI designs, microprocessor architecture and the memory system.

Liu Sheng, born in 1984. Currently an associate professor at the College of Computer, NUDT, China. Received his PhD degree in electronic science and technology from NUDT, China. His main research interests include memory systems and VLSI designs.

An Address Parallel Access Method Supporting Four Reformulated Radix-24FFT

Yang Chao, Chen Haiyan, and Liu Sheng

(CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073)

IEEE 802.15.3c is international unified standard of high-rate wireless personal area networks (high-rate WPANs) to support high data rate applications such as high-definition streaming content downloads, home theater and etc, which needs to finish 512 FFT sizes operations in only 222.2 ns at the sampling rate of 2.592 GHz. To satisfy this demand, some FFT processors adopt parallel PEs and reformulated radix-24FFT algorithm which can reduce the required number of butterfly stages. When parallel PEs are employed, only memory system supporting these PEs parallel accessing operating data and normal order IO can express the full advantages of parallel PEs. According to the accessing law of four reformulated radix-24FFT PEs, this paper designs an address transformation method supporting four reformulated radix-24. And the method in this paper supports normal order IO, which solves the difficulty caused by bit reversal operation of initial or result data, to get a high-throughput design result. The implementation of the single address transformation unit is simple which requires only three two-input XOR gates and one three-input XOR gate. At the same synthesis condition, this method saves area 47% and power 24% compared with the method before. And this method supports continuous flow and in-place operation.

IEEE 802.15.3c; radix-24; FFT; address schedule; parallel; in-place; continuous-flow

2015-07-20；

2016-04-01

国家自然科学基金项目(61472432) This work was supported by the National Natural Science Foundation of China (61472432).

陈海燕(hychen@nudt.edu.cn)

TP332.1