土体率效应对动力锚沉贯深度影响

刘 君， 李 明 治， 韩 聪 聪

( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024；2.上海勘测设计研究院有限公司, 上海 200434 )

土体率效应对动力锚沉贯深度影响

刘 君*1， 李 明 治1,2， 韩 聪 聪1

( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024；2.上海勘测设计研究院有限公司, 上海 200434 )

动力安装锚(简称动力锚)是一种依靠自重进行安装、适用于深海锚泊系统的新型锚固基础．在动力沉贯过程中，土体经受很高的剪应变率(约25 s-1)，因此必须考虑土体率效应影响．总结了以往关于土体率效应的研究成果，整理了常用3种率效应模型中参数的取值范围，采用运动微分方程研究了不同率效应模型参数对动力锚沉贯深度的影响．结果表明：土体率效应会造成动力锚的沉贯深度显著减小，可偏小30%～40%；当率效应参数较大时，锚的沉贯深度对参考应变率的变化比较敏感；摩擦项与端承项的率效应比值对动力锚的沉贯深度影响较大，需要进一步研究该比值的确切取值方法；给出了可以满足任意形状和深度的矩形基础承载力计算公式．

海洋基础；动力锚；率效应；沉贯深度；承载力系数

0 引 言

动力安装锚(dynamically installed anchors，DIAs)简称动力锚，是一种依靠自重进行安装、适用于深海锚泊系统的新型锚固基础[1]．在安装时，首先将锚释放至距离海床表面一定高度处(50～150 m)，然后松开安装锚链，锚在自重作用下贯入海床中．动力锚需要较高的贯入速率(15～25 m/s)以达到较深的沉贯深度，提供足够的抗拔承载力．动力锚的沉贯过程是一个土体经受高剪应变率的过程，因此必须考虑土体率效应影响．

土体率效应是指土的抗剪强度随剪应变率提高而增大的现象[2]．土体率效应大小取决于贯入物体的形状和尺寸、贯入速度和土体的密度、渗透性及超固结比(OCR)等特性．大部分海床土为低渗透性黏土或钙质土，所以对于动力锚的沉贯过程，必须考虑率效应导致的土体强度增加效应．土体率效应对动力锚的沉贯深度影响程度如何，不同的率效应模型又有怎样的影响目前还不得而知．

本文首先总结以往关于土体率效应的研究结果，整理常用3种率效应模型中的参数取值范围．在此基础上，采用基于牛顿第二运动微分方程研究率效应参数对动力锚沉贯深度的影响，旨在揭示动力锚贯入过程中率效应对沉贯深度的影响范围．

1 率效应模型

表征率效应的主要模型有3种：幂函数型、半对数型和反双曲正弦型，如下式所示：

(1a)

(1b)

(1c)

(2)

参考剪应变率的取值应考虑两方面的因素：首先，参考剪应变率应该足够大以确保土体处于不排水状态；其次在保证土体处于不排水状态的前提下，参考剪应变率应足够小，尽可能使剪应变率与参考剪应变率的比值有2～3个量级的变化量，以便对比剪应变率对率效应的影响．

2 已有的率效应研究成果

确定土体强度的试验方法主要有三轴试验、锥形贯入仪试验(CPT)以及十字板剪切试验．近年来，T形和球形贯入仪及动态锥形贯入仪(FFP)也越来越多地用于测量土体强度．不同类型试验用到的贯入仪形状、刚度、粗糙度等也不同，得到的率效应大小有所差别[2-4]，但差别不大．海床土大多为黏性土[5]，所以本文主要总结了黏土和钙质土土体率效应试验结果．

2.1 三轴试验

因三轴试验可严格控制土样的排水状态和外加荷载，所以其能精确测量土的不排水抗剪强度．表1总结了以往的三轴试验结果．从表1可以看出，剪应变率每增长一个量级，土强度的增长范围为8%～20%．根据率效应的定义，可反算得出率效应参数β、λ和λ′的范围分别为0.034～0.079、0.080～0.200和0.027～0.067．

2.2 十字板剪切试验

十字板剪切试验耗时短、操作简单，在确定原位黏土不排水抗剪强度试验中得到了广泛应用[11]．表2列出了几种有代表性的试验结果．

从表2可以看出，除了Schlue等[14]的结果，剪应变率每增长一个量级对应的土强度增长范围为10%～30%．有一点需要说明的是，土体的含水量越高，其峰值强度的率效应会越明显．Schlue等[14]的试验探测了3种含水量的土样，含水量分别是71%、112%、177%．对于含水量为177%的土样，其流动机制近乎于黏滞流体，因此得到的率效应参数比其他结果要大出很多．另一点需要说明的是，恒定的率效应参数(β、λ、λ′)可能会低估高剪应变率情况下土体的率效应[15]．这一点在O′Loughlin等[17]关于鱼雷锚动力沉贯的离心模型试验中也得到了印证，率效应参数会随沉贯速度的增大而增大．因此，当剪应变率的变化范围超过4个量级时，恒定的率效应参数可能不再适合描述土体率效应[15-16]．

表1 三轴试验得到的率效应研究结果

表2 十字板剪切试验得到的率效应研究结果

2.3 T形贯入仪和球形贯入仪试验结果

T形和球形贯入仪作为新型测量土体不排水抗剪强度的贯入仪，在海洋工程领域应用前景广泛．当沉贯深度足够大时，贯入仪周围土体呈全流机制，土体塑性区只在贯入仪附近的区域发展，此时承载力系数为常数．关于T形和球形贯入仪确定土体率效应的试验如表3所示．

如前文所述，同一种土样的率效应会随着试验方法的不同而出现偏差．表3中同一种土样(Burswood黏土)通过T形和球形贯入仪测出的率效应参数有所不同[20]．从表3中可知，剪应变率每增加一个量级对应的土强度增长量范围是10%～38%．

2.4 其他试验

除了上述试验方法，还有一些其他试验方法可以确定土体率效应，如锥形贯入试验、单剪试验以及FFP试验，相关结果如表4所示．锥形贯入仪侧壁摩阻项对应的率效应参数明显高于端承阻力项的率效应参数，因为贯入仪侧壁附近的剪切带要比锥尖处更窄，对应的剪应变率更大[24]．根据Einav等[24]的研究成果，表征率效应的幂函数公式(1a)可改写为

(3)

式中：μ是一个量纲为一的量，端承阻力项和侧壁摩阻项的率效应对应的μ分别取1和(1/β-1)．

从表4中可以得出，除了Dayal等[16]的结果外，剪应变率每增加一个量级对应的土强度提高12%～35%(端承阻力项)．在Dayal等[16]的试验中，土强度范围为3～81 kPa，结果表明强度越低，率效应越明显．强度为3 kPa的土样对应端承阻力项的Δsu=150%；而强度在9～81 kPa的土样对应的Δsu=25%～3%．这一低强度土体率效应显著增长的现象与Schlue等[14]的试验结果相似．这可能是对于某一种黏土，存在一个强度临界值，当土体强度低于该临界值时，土体会呈现明显的黏滞性．

表3 T形和球形贯入仪试验得到的率效应研究结果

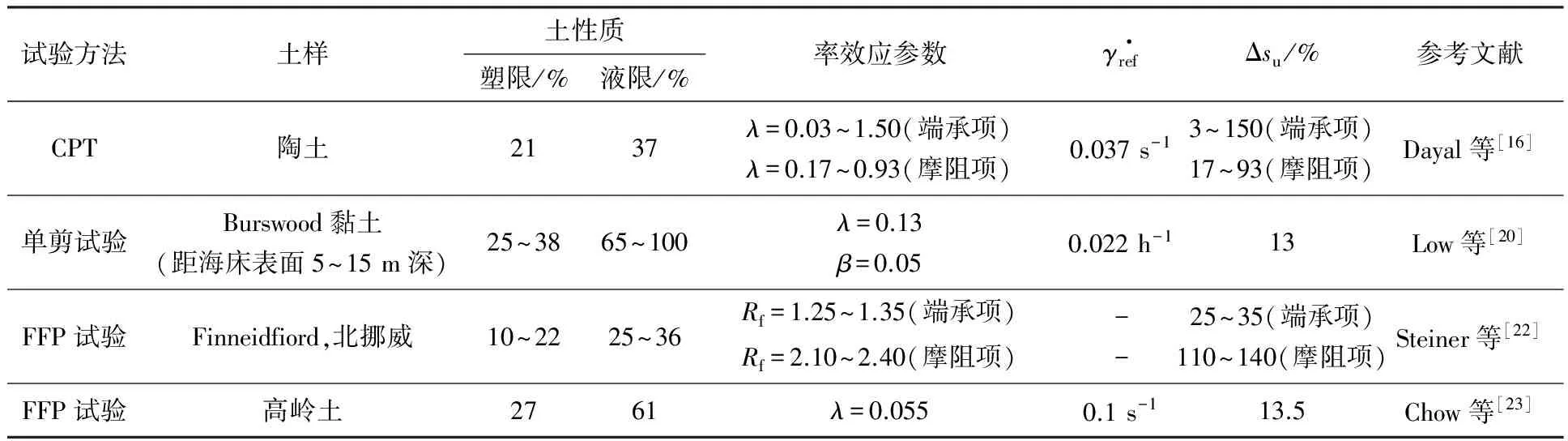
表4 土体率效应的其他类型试验研究结果

2.5 率效应参数取值范围汇总

综上所述，剪应变率每增加一个量级对应的土强度增长范围是8%～38%．影响率效应的因素可归为以下几类：

(1)不同的试验方法由于贯入仪形状、尺寸、粗糙度等不同得到的率效应参数会有所不同；

(2)低强度和低超固结比的土体可能会表现出更明显的率效应[6,12-13,15]；

(3)当剪应变率改变量超过4个量级时，恒定的率效应参数可能会低估土体率效应[15-16]；

(4)可能存在一个临界强度值，当土强度低于该临界值时，土体率效应会显著提高．

通常海洋工程中采用的T形贯入仪尺寸为LT×DT=250 mm×40 mm(LT为T形杆的长度，DT为T形杆的直径)，球形贯入仪直径为113 mm，锥形贯入仪直径为36～44 mm[25]．如果3种贯入仪的贯入速度均为20 mm/s，则贯入仪的应变率范围在0.18 s-1到0.5 s-1．在动力锚沉贯问题数值模拟中，推荐的参考应变率为0.1 s-1[26]．综合表1～4的参考应变率，实际工程中贯入仪的应变率以及本文所要研究动力锚的速度及等效直径等因素，本文选取的参考应变率分别为0.01、0.1、0.5 s-1，尽可能使动力锚的剪应变率与参考剪应变率的比值有2～3个量级的变化量，但不超过4个量级．根据上述总结，不同率效应模型对应的率效应参数的取值范围如表5所示．

表5 应变率参数及参考剪应变率的取值范围

3 率效应对动力锚沉贯深度的影响

3.1 动力锚沉贯深度预测程序的验证

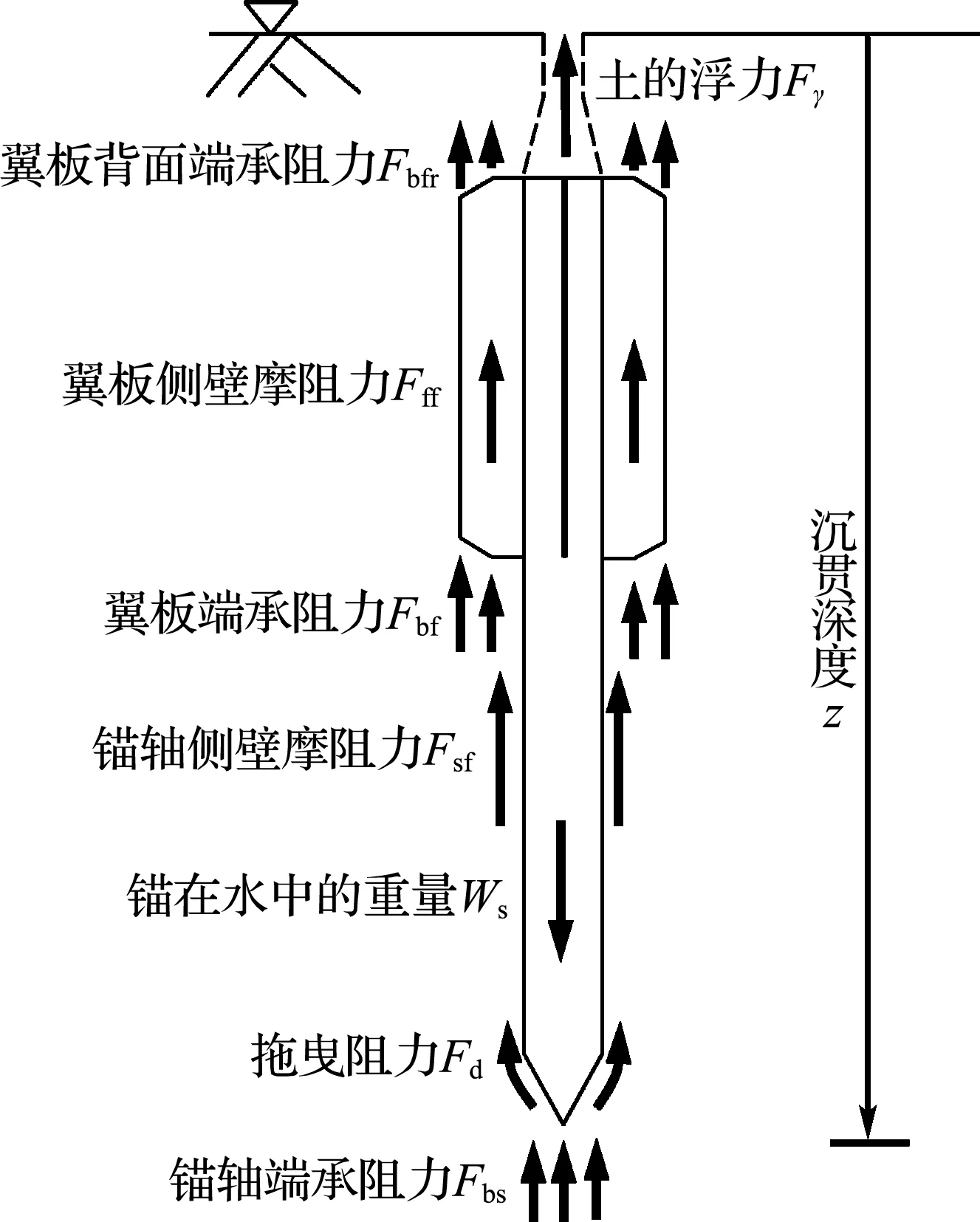
本文仅仅研究土体率效应对锚沉贯深度的影响，故在忽略锚链的附加质量及锚链与水相互作用的情况下，根据True[2]的分析，动力锚在沉贯时的受力如图1所示．

(a) 鱼雷锚

(b) 板形重力安装锚

图1 动力锚沉贯时受到的作用力

Fig.1 Forces acting on dynamically installed anchors during penetrating in clay

依据牛顿第二定律，动力锚沉贯深度的微分方程如下式所示：

(4)

式中：m是锚的质量，t是时间，z是锚在t时刻的沉贯深度，Ws是锚在水中的重量，Fb是锚的垂直于锚轴线方向的横截面受到的端承阻力，Ff是锚侧壁受到的摩阻力，Fγ是土体对锚的浮力，Fd是锚受到的拖曳阻力．

Fb=Ncsu0Ab

Ff=αsu0Af

Fγ=γ′V

Fd=0.5CdρApv2

其中Nc是锚的横截面对应形状的基础承载力系数，对于鱼雷锚和板形重力安装锚的扁平状翼板，可取Skempton[27]给出的深埋条形基础的承载力系数Nc=7.5，对于鱼雷锚的锚轴，可按照Ma等[28]给出的CPT的承载力系数公式，取为12.0；su0是土的静态不排水剪切强度；Ab是t时刻锚没入土中部分的横截面积．

Af是锚的表面积；α是锚土界面摩擦因数，通常取为土体灵敏度的倒数．

γ′是土的浮重度，V是锚挤开土的体积．

Cd是拖曳力系数，通常锚的长细比越大，形状越复杂，Cd值越大，根据Øye[29]给出的研究结果，鱼雷锚的Cd取0.65，根据Kim等[26]给出的结果，板形重力安装锚的Cd取0.63；ρ是土体的浮密度；Ap是锚垂直于轴线方向的投影面积；v是锚在t时刻的速度．

Rf1和Rf2分别表征土体率效应在锚的端承阻力项和侧壁摩阻项中的增强效应．Rf1的计算如式(1)、(2)所示．在计算鱼雷锚和板形重力安装锚的沉贯深度时，式(2)中的d分别代表鱼雷锚的锚轴直径和板形重力安装锚的等效直径(与横截面积等效的圆的直径)．虽然式(3)给出了幂函数形式的Rf1和Rf2的不同，且近几年一些学者[22-23]通过FFP试验得出Rf2/Rf1的取值范围在1.0～2.0，但具体的比值尚无定论．本文的主旨并非探讨动力锚的绝对沉贯深度，因此Rf2/Rf1的具体数值就显得不是特别重要．所以如无特殊说明，以下算例的Rf2/Rf1均根据O′Loughlin等[17]的取值方法取为1.0．

许多学者在式(4)基础上对动力锚的沉贯深度进行了研究，其中O′Loughlin等[17]依据离心机模型试验并结合式(4)做了较多关于鱼雷锚沉贯深度的研究工作．本文首先根据式(4)编制了计算动力锚沉贯深度的Matlab程序，模拟了O′Loughlin 等[17]的两种鱼雷锚的离心机模型试验，并进行了对比，以此验证本文所编制程序的正确性．从图2所示对比结果可以看到两者的吻合程度很好，表明本文所编制程序是准确的．然后根据前文总结的土体率效应参数的取值范围，使用该程序分析了土体率效应参数对鱼雷锚和板形重力安装锚沉贯深度的影响．

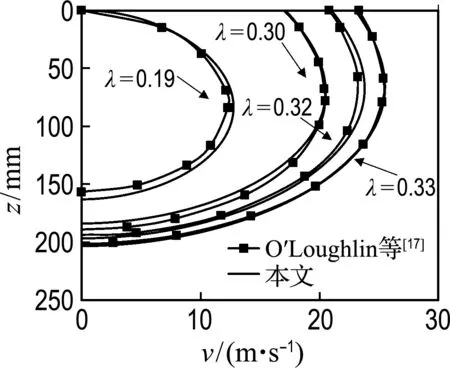
(a) 无尾翼鱼雷锚

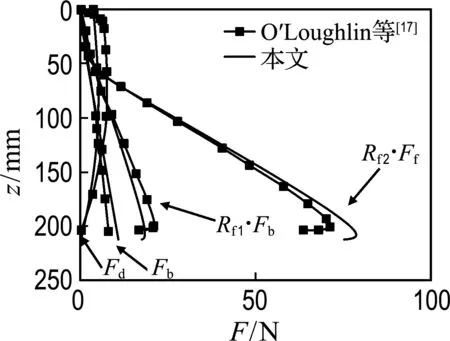
(b) 有尾翼鱼雷锚

图2 鱼雷锚沉贯深度

Fig.2 Penetration depth of torpedo anchors

3.2 率效应参数对鱼雷锚沉贯深度的影响

鱼雷锚的形状及几何参数如图3(a)所示，锚的质量为98 t，锚的初始沉贯速度是20 m/s，土的不排水抗剪强度su0=(5+2z) kPa，土的浮容重为6 kN/m3．

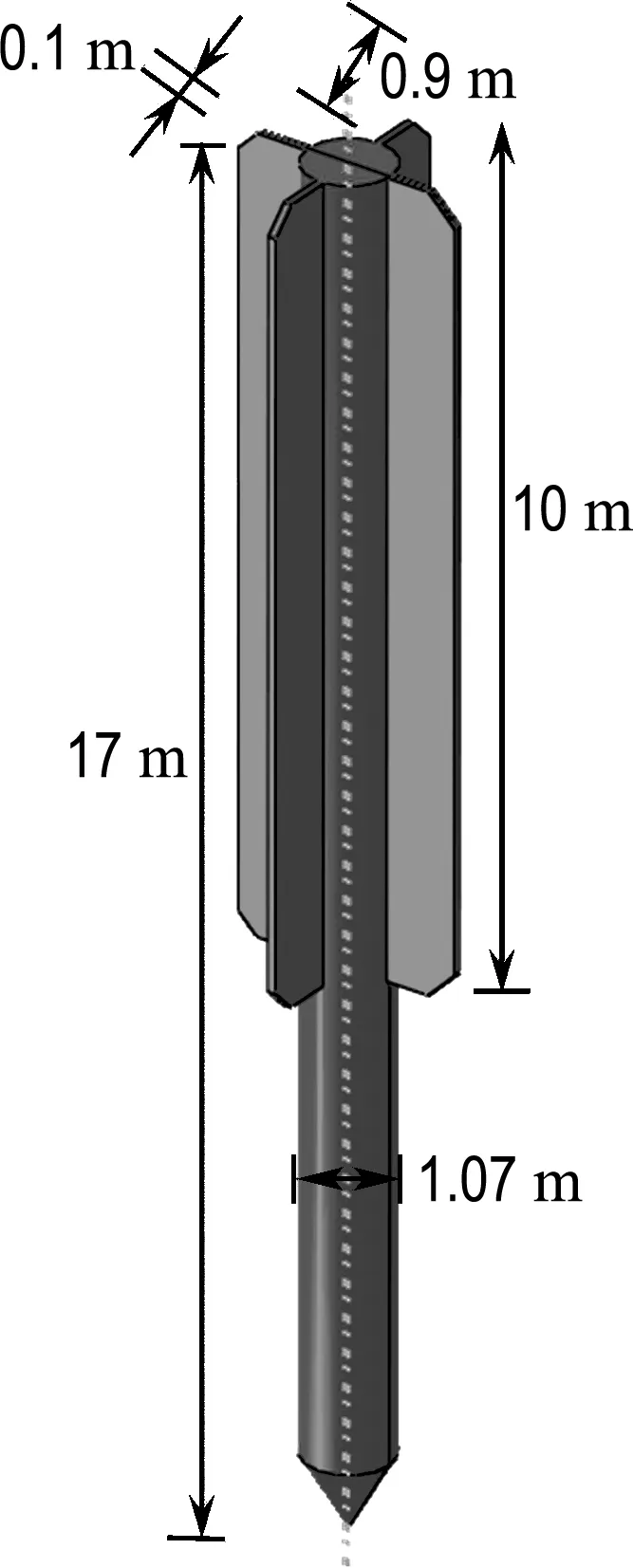
(a) 鱼雷锚 (b) 板形重力安装锚

从表6可以看出，土体率效应参数(β、λ、λ′)对鱼雷锚的沉贯深度影响很大，甚至可达30%以上．锚土之间的摩擦因数α对鱼雷锚沉贯深度影响也较大，从其变化的幅值来看可达27.8%．因此鱼雷锚的沉贯过程分析必须细致考虑土体率效应和锚土界面摩擦效应对锚的沉贯深度的影响．

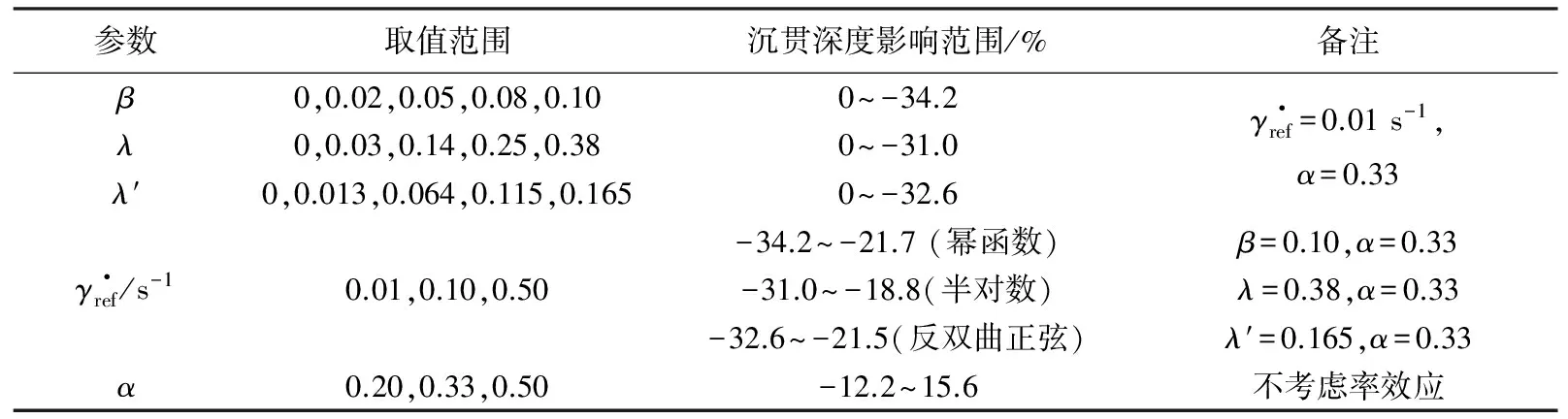
表6 鱼雷锚沉贯深度变化范围

(a) ref=0.1 s-1 (b) β=0.05 (c) α=0.33

前文述及，由于鱼雷锚的翼板厚宽比接近0.1，很多学者将翼板受到的端承阻力按照深埋条形基础的承载力进行计算，并使用Skempton[27]给出的承载力系数Nc=7.5计算动力锚沉贯过程中翼板受到的端承阻力．

然而通过梳理近20年来其他学者[30-32]的研究成果发现：深埋条形基础的承载力系数并非7.5．如图5所示，Skempton[27]认为条形基础埋深超过4倍基础宽度时，即为深埋情况，承载力系数达到7.5后不再增长．而Salgado等[30]、Edwards等[31]以及Quoc[32]给出的结果是：条形基础的埋深达到了5倍基础宽度时，其承载力系数仍然有增长的趋势，且高出7.5较多．因此本文采用ABAQUS有限元软件计算了长宽比为0.05、0.10 的矩形基础以及条形基础在较大埋深(最大埋深达到了150倍基础宽度)情况下的承载力系数．

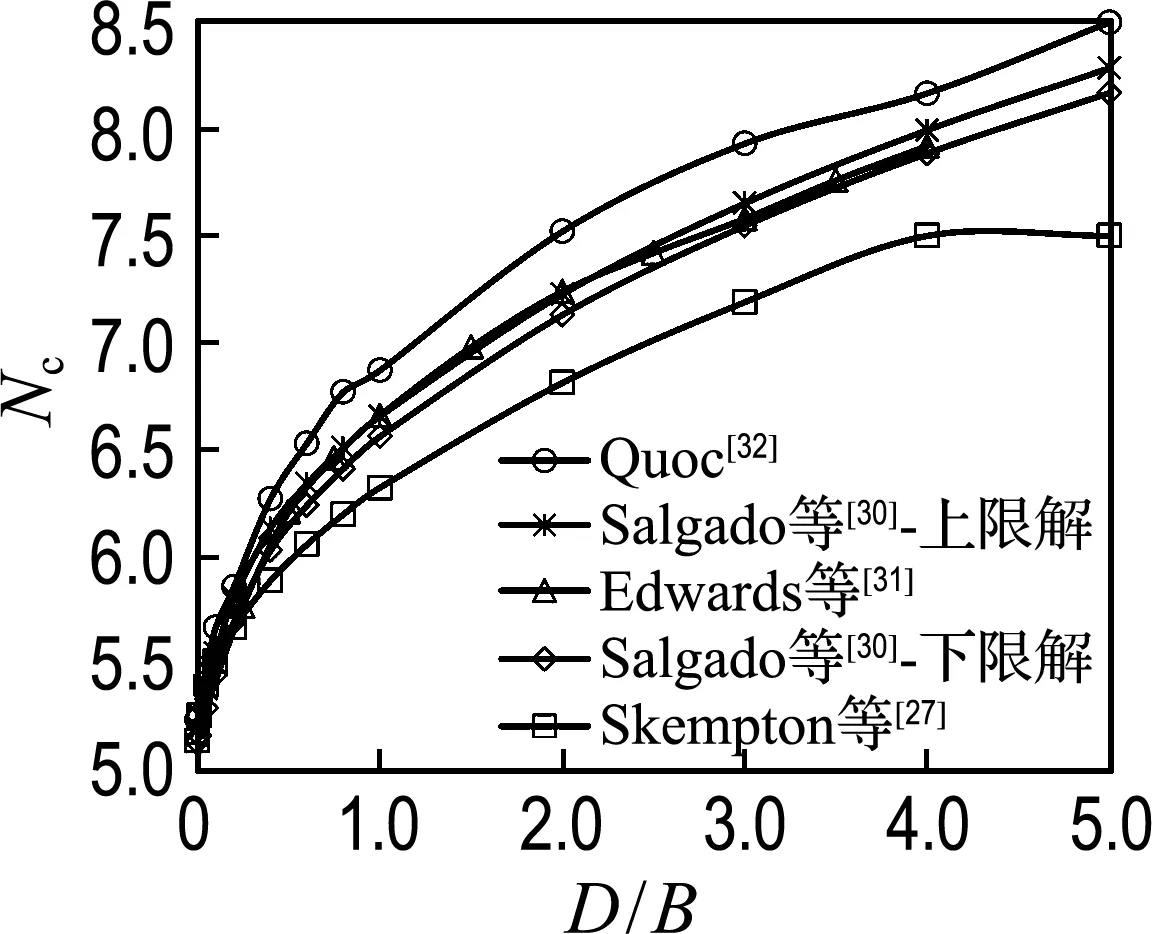
图5 不同埋深情况的条形基础承载力系数

由于对称性，采用1/4模型计算，有限元网格如图6所示．土体采用理想弹塑性材料，满足Tresca屈服准则；基础的刚度通常远大于土体，因此将基础视为刚体．通过网格收敛性分析，采用B/50(B为基础宽度)作为土体最小网格尺寸，既能满足精度要求又能有效控制计算时间．基础棱角处的土体的塑性应变较大，因此棱角处土体网格密度较大，而远离该区域的土体网格密度较小．经过比较分析，土体单元类型选择一阶完全积分的六面体杂交单元(C3D8H)．土体与基础之间接触光滑．土体底面为铰支约束，侧壁为滚轴约束．加载方式为给基础一个向下的位移荷载，直至土体的抗力达到一个屈服平台为止．图7所示为B/L= 0.05，D/B= 10情况下承载力系数随着基础量纲一位移的变化情况(L为基础长度，D为基础上表面的埋深)．图中的横坐标为基础的量纲一位移，E为土体的弹性模量，δ为基础的位移．

所有工况的承载力系数结果如图8中的散点所示．依据计算结果采用Origin拟合了一个计算薄板基础在较大埋深情况下的承载力系数计算公式，如下式所示：

Nc=5.14×{1.022+0.063B/L+c1ln(1+c2(D/B))}

(5)

其中

图8 矩形基础的极限承载力系数

3.3 率效应参数对板形重力安装锚沉贯深度的影响

板形重力安装锚形状及几何参数如图3(b)所示．锚质量为39.8 t，锚的初始沉贯速度是20 m/s．土体不排水抗剪强度su0=(2.4+1.1)zkPa，土体浮容重为6 kN/m3．率效应参数的取值范围及对沉贯深度的影响如表7所示，表中的沉贯深度变化范围的计算方法与鱼雷锚的相同．

从表7可以看出，土体率效应参数(β、λ、λ′)对板形重力安装锚的沉贯深度影响更大，甚至可达40%以上．锚土之间的摩擦因数α对板形重力安装锚沉贯深度影响也较大，从其变化的幅值来看可达22.0%．因此板形重力安装锚的沉贯过程分析必须细致考虑土体率效应和锚土界面摩擦效应对锚的沉贯深度的影响．

表7 板形重力安装锚沉贯深度变化范围

(a) ref=0.10 s-1

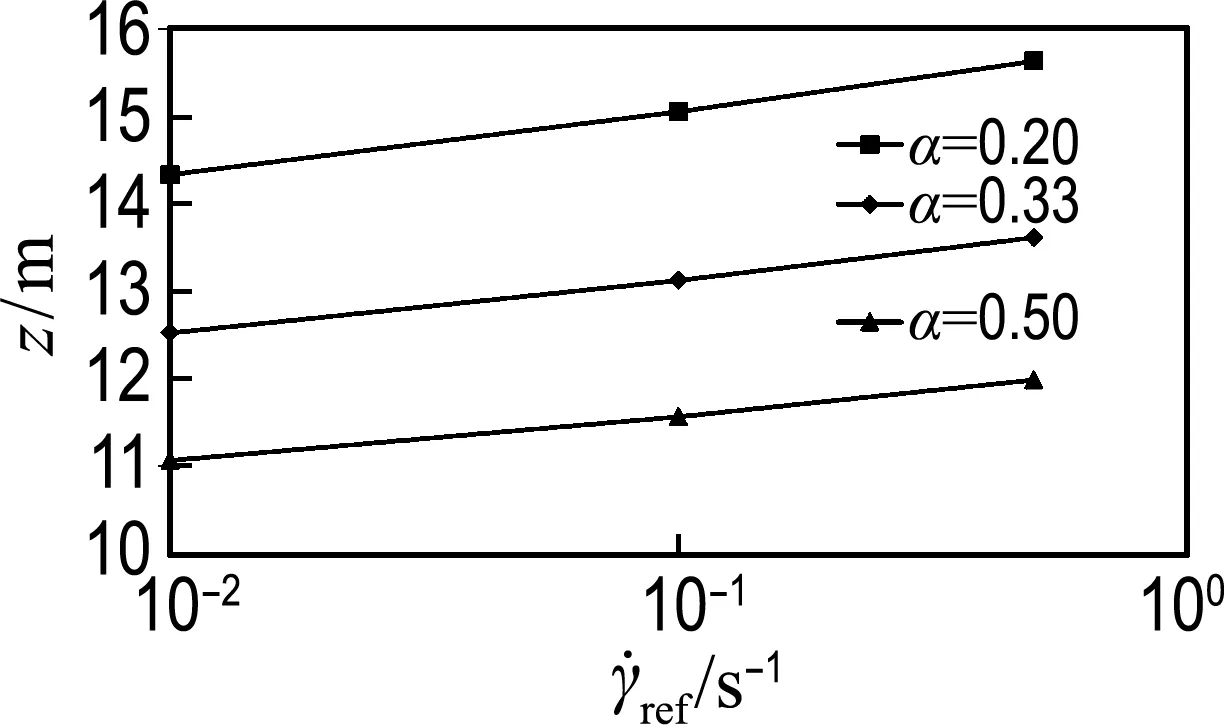
(b)λ=0.14

(c)α=0.33

图9 率效应参数的相互影响(板形重力安装锚)

Fig.9 The mutual effect of strain-rate effect parameters (gravity installed plate anchor)

4 结 论

(1)不论是鱼雷锚，还是板形重力安装锚，土体率效应均会造成锚的沉贯深度偏小31%～42.1%，所以在评估鱼雷锚和板形重力安装锚的沉贯深度时，必须考虑率效应．

(2)当率效应参数(β、λ、λ′)较大时，锚的沉贯深度对参考应变率的变化比较敏感．因此当率效应参数较大时，需谨慎选择参考应变率．

(3)摩擦项和端承项的率效应比值Rf2/Rf1对鱼雷锚和板形重力安装锚的沉贯深度影响较大，但目前关于Rf2/Rf1的取值尚无定论，因此需要进一步研究Rf2/Rf1的确切取值方法．

(4)目前常用的率效应模型均可以很好地描述土体率效应，在本文所研究的参数范围内，3种模型给出基本一致的影响．因此选择任何一个模型来描述土体率效应对沉贯深度的影响均可．但计算翼板的端承阻力时，采用以往的条形基础的承载力系数是偏于危险的．

(5)给出了可以满足任意形状和深度的矩形基础承载力计算公式．

[1] RICHARDSON M D, O′LOUGHLIN C D, RANDOLPH M F,etal. Setup following installation of dynamic anchors in normally consolidated clay [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(4):487-496.

[2] TRUE D G. Undrained vertical penetration into ocean bottom soils [D]. Berkeley: University of California, 1976.

[3] GRAHAM J, CROOKS J H, BELL A L. Time effects on the stress-strain behaviour of natural soft clays [J]. Géotechnique, 1983, 33(3):327-340.

[4] LEHANE B M, O′LOUGHLIN C D, RANDOLPH M F,etal. Rate effects on penetrometer resistance in kaolin [J]. Géotechnique, 2009, 59(1):41-52.

[5] RANDOLPH M, CASSIDY M, GOURVENEC S,etal. Challenges of offshore geotechnical engineering [C] // Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering: Geotechnology in Harmony with the Global Environment. Rotterdam: Millpress Science Publishers, 2005:123-176.

[6] SHEAHAN T C, LADD C C, GERMAINE J T. Rate-dependent undrained shear behavior of saturated clay [J]. Journal of Geotechnical Engineering-ASCE, 1996, 122(2):99-108.

[7] YIN Z Y, HICHER P Y, RIOU Y,etal. An elasto-viscoplastic model for soft clay [J]. Geotechnical Special Publication, 2006(150):312-319.

[8] YIN Zhenyu, KARSTUNEN M, HICHER P Y. Evaluation of the influence of elasto-viscoplastic scaling functions on modelling time-dependent behaviour of natural clays [J]. Soils and Foundations, 2010, 50(2):203-214.

[9] TORISU S S, PEREIRA J M, DE GENNARO V,etal. Strain-rate effects in deep marine clays from the gulf of Guinea [J]. Géotechnique, 2012, 62(9):767-775.

[10] PALIX E, WU H, CHAN N,etal. Liwan 3-1:How Deepwater Sediments from South China Sea Compare with Gulf of Guinea Sediments [C]. Houston: Offshore Technology Conference, 2013:OTC-24010-MS.

[11] BISCONTIN G, PESTANA J M. Influence of peripheral velocity on vane shear strength of an artificial clay [J]. Geotechnical Testing Journal, 2001, 24(4):423-429.

[12] AUBENY C P, SHI Han. Effect of rate-dependent soil strength on cylinders penetrating into soft clay [J]. IEEE Journal of Oceanic Engineering, 2007, 32(1):49-56.

[13] BOUKPETI N, WHITE D, RANDOLPH M,etal. Characterization of the solid-fluid transition of fine-grained sediments [C] // Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering 2009, OMAE2009. New York: ASME, 2009:293-303.

[14] SCHLUE B F, MOERZ T, KREITER S. Influence of shear rate on undrained vane shear strength of organic harbor mud [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(10):1437-1447.

[15] ABELEV A, VALENT P. Strain-rate dependence of strength of the gulf of Mexico soft sediments [J]. IEEE Journal of Oceanic Engineering, 2013, 38(1):25-31.

[16] DAYAL U, ALLEN J H. The effect of penetration rate on the strength of remolded clay and sand samples [J]. Canadian Geotechnical Journal, 1975, 12(3):336-348.

[17] O′LOUGHLIN C D, RICHARDSON M D, RANDOLPH M F,etal. Penetration of dynamically installed anchors in clay [J]. Géotechnique, 2013, 63(11):909-919.

[18] CHUNG S F, RANDOLPH M F, SCHNEIDER J A. Effect of penetration rate on penetrometer resistance in clay [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(9):1188-1196.

[19] YAFRATE N J, DEJONG J T. Influence of penetration rate on measured resistance with full-flow penetrometers in soft clay [J]. Geotechnical Special Publication, 2007(173):1-10.

[20] LOW H E, MAYNARD M L, RANDOLPH M F,etal. Geotechnical characterisation and engineering properties of Burswood clay [J]. Géotechnique, 2011, 61(7):575-591.

[21] GANESAN S A, BOLTON M D. Characterisation of a high plasticity marine clay using a T-bar penetrometer [J]. Underwater Technology, 2013, 31(4):179-185.

[22] STEINER A, KOPF A J, L′HEUREUX J,etal. In situ dynamic piezocone penetrometer tests in natural clayey soils - a reappraisal of strain-rate corrections [J]. Canadian Geotechnical Journal, 2014, 51(3):272-288.

[23] CHOW S H, O′LOUGHLIN C D, RANDOLPH M F. Soil strength estimation and pore pressure dissipation for free-fall piezocone in soft clay [J]. Géotechnique, 2014, 64(10):817-827.

[24] EINAV I, RANDOLPH M. Effect of strain rate on mobilised strength and thickness of curved shear bands [J]. Géotechnique, 2006, 56(7):501-504.

[25] LOW H E, LUNNE T, ANDERSEN K H,etal. Estimation of intact and remoulded undrained shear strengths from penetration tests in soft clays [J]. Géotechnique, 2010, 60(11):843-859.

[26] KIM Y H, HOSSAIN M S. Dynamic installation of OMNI-Max anchors in clay:numerical analysis [J]. Géotechnique, 2015, 65(12):1029-1037.

[27] SKEMPTON A W. The bearing capacity of clays [C] // Proceedings of Building Research Congress. London: [s. n.], 1951:180-189.

[28] MA Hongliang, ZHOU Mi, HU Yuxia,etal. Interpretation of layer boundaries and shear strengths for soft-stiff-soft clays using CPT data:LDFE analyses [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(1):04015055.

[29] ØYE I. Simulation of trajectories for a deep penetrating anchor:Report No. 250:2000 [R]. Trondheim:CFD Norway, 2000.

[30] SALGADO R, LYAMIN A V, SLOAN S W,etal. Two- and three-dimensional bearing capacity of foundations in clay [J]. Géotechnique, 2004, 54(5):297-306.

[31] EDWARDS D H, ZDRAVKOVIC L, POTTS D M. Depth factors for undrained bearing capacity [J]. Géotechnique, 2005, 55(10):755-758.

[32] QUOC V N. Numerical modelling of the undrained vertical bearing capacity of shallow foundations [D]. Toowoomba: University of Southern Queensland, 2008.

Influence of soil strain-rate effect on embedment depth of dynamically installed anchors

LIU Jun*1, LI Mingzhi1,2, HAN Congcong1

( 1.State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China； 2.Shanghai Investigation, Design & Research Institute Company, Limited, Shanghai 200434, China )

Dynamically installed anchors, which are installed through self-weight, are newly developed anchors applied to deep-water mooring systems. During the dynamical embedment procedure, the soil is subjected to high shear strain-rate (about 25 s-1). Hence, the soil strain-rate effect should be necessarily taken into consideration. The ranges of soil strain-rate parameters of three commonly used models are summarized based on the published literatures referred to soil strain-rate effect, and the influence of strain-rate effect on the embedment depth of dynamically installed anchors based on the motion differential equation is discussed in the following. The research results indicate that the embedment depth of dynamically installed anchors would drastically decrease (30%-40%) due to the soil strain-rate effect. The embedment depth is sensitive to the reference strain-rate when strain-rate parameters are in high values. The shear strain-rate effect ratio of the frictional resistance to the end bearing resistance has significant effect on the embedment depth and further investigation is necessitated to define this ratio. A new formula is proposed to calculate the bearing capacity of rectangular footing with any shape and embedment depth.

offshore foundation; dynamically installed anchors; strain-rate effect; embedment depth; bearing capacity factor

1000-8608(2017)01-0068-10

2016-07-09；

2016-11-20．

国家自然科学基金资助项目(51479027，51539008).

刘 君*(1972-)，男，博士，教授，E-mail:junliu@dlut.edu.cn；李明治(1990-)，男，硕士生，E-mail:731426627@qq.com；韩聪聪(1990-)，女，博士生，E-mail:1059281811@qq.com.

TU47

A

10.7511/dllgxb201701010