基于遗传算法的负刚度装置优化布置

孙 彤， 李 宏 男*,2， Satish Nagarajaiah

( 1.大连理工大学 建设工程学部， 辽宁 大连 116024；2.沈阳建筑大学 土木工程学院， 辽宁 沈阳 110168；3.莱斯大学 土木与环境工程系， 得克萨斯 休斯顿 77005 )

基于遗传算法的负刚度装置优化布置

孙 彤1， 李 宏 男*1,2， Satish Nagarajaiah3

( 1.大连理工大学 建设工程学部， 辽宁 大连 116024；2.沈阳建筑大学 土木工程学院， 辽宁 沈阳 110168；3.莱斯大学 土木与环境工程系， 得克萨斯 休斯顿 77005 )

针对一种新型轨道式负刚度装置(negative stiffness device，NSD)提出了一种基于遗传算法的优化布置数学模型，该模型同时考虑NSD在加速度控制上的优势和位移控制上的劣势，设定5组加权系数组合，考察不同优化侧重下的控制效果．以某10层结构为算例，通过对比负刚度装置和传统阻尼器控制效果，得到最优加权系数组合；通过对比5组加权系数组合，得到负刚度装置优化布置基本原则．

负刚度装置；遗传算法；优化布置；高层结构

0 引 言

负刚度控制是结构控制领域近年来比较热门的一种控制方式，国内外一些学者提出了不同的负刚度装置(negative stiffness device，NSD)[1-5]，结合黏滞型被动阻尼器的使用，其能够有效抑制弱化结构导致的位移增大，提供较好的控制效果．目前，采用负刚度装置布置在隔震层的控制方案较多[6-8]，其本质是隔震系统的改善，但这种布置仅对于低层和多层结构比较适用[9]．随着经济发展，高层、超高层结构已经随处可见，传统负刚度控制的局限性已十分明显．

本文针对新型轨道式NSD在高层结构控制中的布置提出一种优化目标函数，利用遗传算法根据不同组合加权系数的目标函数进行优化布置，研究不同组合加权系数对优化结果的影响，最后给出高层结构中负刚度装置的布置原则．

1 理论模型

1.1 轨道式NSD力学模型

轨道式NSD是位移型控制装置，结构如图1所示(照片为试验装置)，预压缩弹簧将滚轮压在轨道块上，轨道块的起伏会给滚轮一个垂直于弹簧方向的负刚度分力，其力学模型为

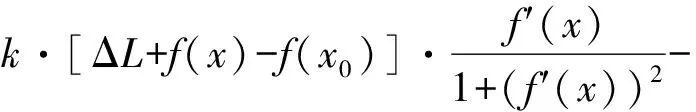
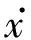
x．

)μNcos2α

(1)

式中：第一项为负刚度力，与弹簧刚度、预压缩量、装置变形和轨道形状有关；第二项为摩擦力，方向由速度方向决定．k为轨道式NSD中预压缩弹簧刚度，ΔL为弹簧预压缩量，f(x)为轨道母线方程，f′(x)为f(x)的导数，x0为滚轮在轨道块上的初始位置，μ为摩擦因数，N为弹簧弹力，

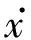
x．

为滚轮在x处速度，sgn为符号函数，α为滚轮和轨道块接触点处切线与X轴夹角．轨道式NSD力-位移曲线如图2所示，可以看出试验结果与数值模拟吻合较好，说明数学模型准确、有效．

NSD的设置会降低结构刚度，导致结构位移响应增大．研究表明[5]，20%阻尼比的线性黏滞阻尼器能够有效控制这种影响．

1.2 结构计算模型

地震作用下n个自由度的受控结构运动方程为

M

x．．

+C

x．

+Kx=MI

x．．

g+Eun+Eud

(2)

式中：M、C和K分别为受控结构n×n维质量、阻尼和刚度矩阵；

x．．

、

x．

和x分别为受控结构相对于地面的加速度、速度和位移反应向量；I为单位列向量；

x．．

g为地震动加速度向量；un、ud分别为r维NSD控制力和阻尼器控制力向量；E为n×r维NSD控制系统位置矩阵．

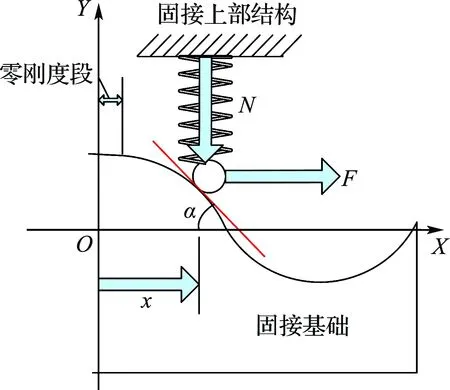
(a) 结构图

(b) 照片

图1 轨道式NSD结构图与照片

Fig.1 Diagram and photo of curve-based NSD

图2 轨道式NSD力-位移曲线

2 基于遗传算法的优化设计

2.1 优化变量

选择表示NSD安装位置的矩阵P1×n作为优化变量，n代表结构层数，未布置NSD的楼层用0表示，布置NSD的用1表示．阻尼器数量确定的问题中，主要优化数字1的位置．如一栋5层楼房，在1、3层布置负刚度装置，则位置矩阵

P=(1 0 1 0 0)

(3)

2.2 目标函数

针对负刚度装置降低结构刚度、增大位移反应的特点，设计兼顾加速度反应和位移反应的目标函数如下：

(4)

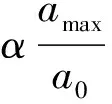
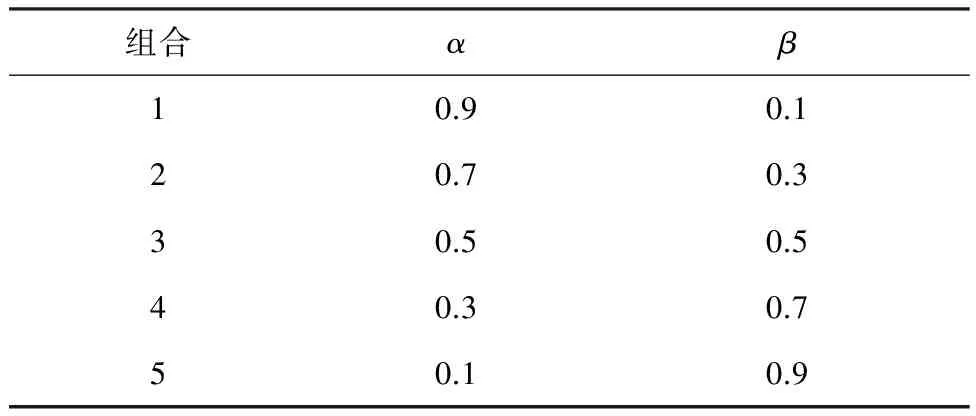
表1 加权系数组合

2.3 选择算子

选择算子的作用是筛选父代群体中哪些个体能够把自身基因传递到子代群体．本文采用轮盘赌选择方法，n个个体构成的种群中，第i个个体适值函数值为fi，其被选中的概率为

(5)

2.4 交叉算子

生物进化中基因会通过交配重组产生新的个体，遗传算法中使用交叉算子来模拟这个过程．本文采用两点交叉，即在父代基因编码中随机设置两个点，交换基因首尾两段染色体．

图3 交叉算子示意图

Fig.3 Diagram of crossover operator

3 数值分析

3.1 工程概况

某10层钢筋混凝土结构，自振周期为1.1 s，阻尼为5%．结构各层质量和刚度如表2所示．地震动荷载选取3条最不利实际地震加速度记录[10]：F4 (El Centro，N69W，1979)、F5(Taft，N21E，1952)和N2(Gengma，SOOE，1988)．峰值加速度均设为40 m/s2，相当于烈度为8度地区大震情况．不失一般性，选择负刚度比在30%～40%[11]，负刚度装置出力峰值为14 kN，其对应位移为15 mm．作为对比，使用阻尼系数为60 kN·s/m 的阻尼器对结构进行均布控制[12]．

表2 框架结构参数

3.2 结果分析

应用遗传算法优化过程中，种群初始规模设为30，变异概率为0.2，进化代数为50代．优化布置结果如表3所示，1代表布置轨道式NSD，0代表未布置．组合1～5的目标函数值依次为0.299 6、0.378 9、0.422 3、0.482 3、0.488 3．可以看出，随着优化加权系数变化，阻尼器布置有相对稳定的趋势：加速度优化权重越大，阻尼器布置的楼层越靠下；位移优化权重越大，阻尼器布置的楼层越靠上．

表3 优化布置结果

5种优化方案下，各层层间位移峰值与传统阻尼器控制下结构响应对比如图4所示．组合1和组合2在结构中下部的层间位移高于传统阻尼器的控制结果，组合3/4/5在结构上部的层间位移大于传统阻尼器，不难看出，层间位移增大的楼层与负刚度装置的布置楼层一致，符合负刚度装置会弱化结构导致层间位移增大的规律[13]．如图5所示，结构加速度反应包络图随α降低而向右扩张，采用相近的加权系数组合会得到相近的优化结果，表明目标函数设计合理，能够有效调节优化侧重点．

图4 各层层间位移峰值

受控结构在各种控制方案下反应峰值和减震率如表4所示，当α>β时，结构加速度反应峰值得到极大控制，代价是层间位移反应峰值比采用传统阻尼器控制时更大；当α≤β时，结构位移反应峰值比采用传统阻尼器时更小，尤其是组合3和组合4的优化结果，结构加速度反应峰值和位移反应峰值相较传统阻尼器均有较大程度降低．可见，负刚度装置增大结构位移反应的问题能够通过优化布置有效解决．

图5 各层加速度峰值

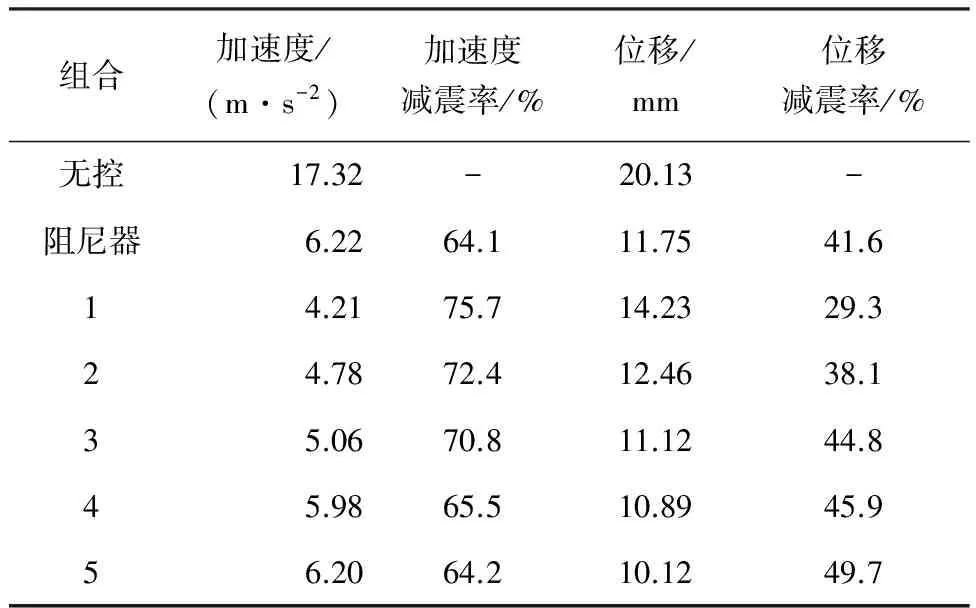
表4 受控结构减震效果

4 结 论

(1)高层结构中负刚度装置应布置在结构中下部，且应连续布置．

(3)除了应用于隔震结构控制，负刚度装置也可以有效控制高层结构的地震反应，通过优化布置可以在保证控制效果的前提下克服其增加位移反应的缺点．

[1] PASALA D, SARLIS A, NAGARAJAIAH S,etal. Adaptive negative stiffness:new structural modification approach for seismic protection [J]. Journal of Structural Engineering, 2013, 139(7):1112-1123.

[2] IEMURA H, PRADONO M H. Advances in the development of pseudo-negative-stiffness dampers for seismic response control [J]. Structural Control & Health Monitoring, 2009, 16(7/8):784-799.

[3] IEMURA H, IGARASHI A, PRADONO M H,etal. Negative stiffness friction damping for seismically isolated structures [J]. Structural Control & Health Monitoring, 2006, 13(2/3):775-791.

[4] 段玉新. 磁致伸缩负刚度阻尼器设计研究[D]. 武汉:华中科技大学, 2011.

DUAN Yuxin. The research on the design of the magnetostrictive negative stiffness damper [D]. Wuhan:Huazhong University of Science & Technology, 2011. (in Chinese)

[5] SARLIS A A, PASALA D T, CONSTANTINOU M C,etal. Negative stiffness device for seismic protection of structures [J]. Journal of Structural Engineering, 2013, 139(7):1124-1133.

[6] IEMURA H, PRADONO M H. Application of pseudo-negative stiffness control to the benchmark cable-stayed bridge [J]. Structural Control & Health Monitoring, 2003, 10(3/4):187-203.

[7] ATTARY N, SYMANS M, NAGARAJAIAH S,etal. Experimental shake table testing of an adaptive passive negative stiffness device within a highway bridge model [J]. Earthquake Spectra, 2015, 31(4):2163-2194.

[8] VITI S, CIMELLARO G P, REINHORN A M. Retrofit of a hospital through strength reduction and enhanced damping [J]. Smart Structures and Systems, 2006, 2(4):339-355.

[9] 中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011—2010[S]. 北京:中国建筑工业出版社, 2010.

Ministry of Housing and Urban-Rural Development of the People′s Republic of China. Code for Seismic Design of Buildings: GB 50011-2010 [S]. Beijing:China Architecture & Building Press, 2010. (in Chinese)

[10] 谢礼立,翟长海. 最不利设计地震动研究[J]. 地震学报, 2003, 25(3):250-261.

XIE Lili, ZHAI Changhai. Study on the severest real ground motion for seismic design and analysis [J]. Acta Seismologica Sinica, 2003, 25(3):250-261. (in Chinese)

[11] 纪 晗,熊世树,袁 涌. 基于负刚度原理的结构隔震效果分析[J]. 华中科技大学学报(自然科学版), 2010, 38(2):76-79.

JI Han, XIONG Shishu, YUAN Yong. Analyzing vibration isolation effect of structures using negative stiffness principle [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(2):76-79. (in Chinese)

[12] 付 杰. 负刚度磁流变阻尼器减震系统的理论与实验研究[D]. 武汉:华中科技大学, 2014.

FU Jie. Theoretical and experimental studies on vibration control system of negative stiffness magnetorheological damper [D]. Wuhan: Huazhong University of Science and Technology, 2014. (in Chinese)

[13] PASALA D T R, SARLIS A A, REINHORN A M,etal. Apparent weakening in SDOF yielding structures using a negative stiffness device: Experimental and analytical study [J]. Journal of Structural Engineering, 2015, 141(4):04014130.

Optimal placement of negative stiffness device using genetic algorithm

SUN Tong1, LI Hongnan*1,2, Satish Nagarajaiah3

( 1.Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China； 2.School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China； 3.Department of Civil and Environmental Engineering, Rice University, Houston 77005, USA )

A mathematic model of optimal placement for a new type of curve-based negative stiffness device (NSD) is put forward based on genetic algorithm (GA). This model gives consideration to both the advantage of NSD in acceleration control and the disadvantage in displacement control. Five combination modes of weighting coefficients are given to investigate the control effects in different optimization strategies. A 10-story structure is used numerically as an example. Optimum combination of weighting coefficients is found by comparing the control effect of NSD and traditional damper. Basic principles of the optimal placement of NSD are presented by comparing five combination modes of weighting coefficients.

negative stiffness device; genetic algorithm; optimal placement; high-rise structure

1000-8608(2017)01-0087-05

2016-08-31；

2016-11-09．

国家自然科学基金资助项目(51261120375).

孙 彤(1986-)，男，博士生，E-mail:suntong009@mail.dlut.edu.cn；李宏男*(1957-)，男，博士，长江学者奖励计划特聘教授，博士生导师，E-mail:hnli@dlut.edu.cn.

TH212；TH213.3

A

10.7511/dllgxb201701012