基于Legendre多项式的板形模式识别优化仿真及应用
2021-12-10王海霞王庆华
王海霞,王庆华
(1.苏州大学 应用技术学院,江苏 苏州 215325;2.华东交通大学 交通运输与物流学院,南昌 330013;3.洛阳有色金属加工研究院,河南 洛阳 471003)
铜板带产品因性能良好被广泛应用于电缆、电子芯片和家电等多种领域,对国民经济的发展有着举足轻重的影响.近年来,随着铜材料超强超导化和产品极端化等新趋势的出现,对铜板带产品的几何精度要求也越来越高,其中板形控制精度是产品几何精度中重要的衡量指标,通常要求板形精度误差在1%以内.在板形精度实现过程中,板形缺陷模式的识别是板形控制系统最主要的组成部分,影响着系统的控制性能,起着至关重要的作用[1].目前使用的板形识别模式算法多种多样,最常用的是最小二乘法,但因其算法局限,应用效果和范围受一定的限制,无法满足市场对铜板带产品质量日趋严格的要求.
1 板形模式识别算法的现状
板形模式识别是根据检测到的板宽方向上残余应力分布信号(定义为σ(i),i为板形测量仪分区个数)计算板形的特征参数值,利用特定的识别算法提取反映当前板形形态的模式类型[2],判断带材的板形缺陷类型.通常这些缺陷形态较为复杂,不适合用作控制参数.因此,根据工艺和板形精度要求,定义相应的板形缺陷类型作为基本参考识别模式.在进行板形控制时,利用实测残余应力信号识别到的板形缺陷,通过一种或几种基本模式组合进行表达,并用特征参数来标定.这种方式便于数学描述,可直接作用于控制环节进行不同要求的板形控制.
板形控制系统是大滞后非线性系统.在板形实测应力识别过程中,误差或计算量过大都会严重影响控制效果,为此先后出现了最小二乘法、正交多项式分解法、模糊识别法及基于小波分析和神经网络等多种识别方法来完善和修正板形缺陷识别[3].最小二乘法板形模式识别是在最小二乘原理上将板形调节偏差采用多项式来表达的一种回归分解方法,假设残余应力信号是非线性关系,通过一个多项式拟合模型来进行拟合,如式(1)所示:
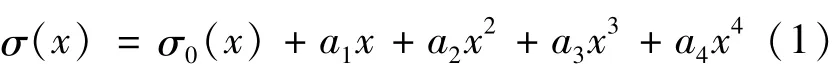
式中:x为沿板宽方向的位置坐标值;σ(x)为板形调节偏差;σ0,a1,a2,a3,a4为板形识别后的调节系数;a1x为线性板形缺陷部分,通过调节轧辊倾斜机构来消除;a2x2为板形缺陷中二次曲线分量,通过调整轧机工作辊弯辊机构或CVC辊位置来消除;a3x3+a4x4为高次板形缺陷分量,通过轧机的分段冷却控制系统来消除.
新一代高速宽幅轧机出现后,最小二乘法的应用出现了拟合后的回归系数物理意义不明确,对四分浪、边中浪和高次浪缺陷识别不准确,抗干扰差,无法确定逼近阶数n的大小,逼近精度有限等缺点.由于得不到精确的板形特征参数,最小二乘法不利于把握板形控制措施[3-4].之后早期的Legendre多项式回归方法同时包含一次项和三次项,要求设备具有三次项板形调整机构,对板形控制设备提出了更高的要求.
随着板形模式识别技术的发展,先后又出现了模糊分类法和神经网络法等智能板形识别方法.模糊分类法的在线识别快速稳定,解决了板形识别中抗干扰能力差的问题,但识别精度较低,不能满足板形精度指标要求[5].神经网络属于全局逼近型算法,结构简单易于实现,在故障诊断和模式识别方面被广泛应用.目前应用于板形缺陷识别的神经网络法有两种:直接识别法(EBP)和基于模糊距离的间接识别法(FBP)[6].神经网络的算法结构简单,但必须用静态时间建模代替动态空间建模,且识别时间模式的泛化能力差、学习速度慢[7].其另一个不可忽视的问题是学习时间过长会出现过拟合或过学习的情况,不利于泛化能力的增强,导致控制效果不理想[8].除上述几种比较常用的方法,近几年出现的基于图像处理和小波分析等新型识别方法,也可得到比较好的识别结果,但对控制系统的算力和存储空间有较高的要求.
为了解决识别中逼近精度有限和阶数不确定的问题,以及避免一次项和三次项同时出现带来的板形调节矛盾,并能准确简便地识别多种板形缺陷,本文在最小二乘基函数基础上对Legendre多项式进行优化,根据来料板形和控制要求选择多项式,采用Matlab仿真得到多项式特征参数,代替固定多项式和参数.该优化算法在安徽楚江650 mm铜精轧机上进行系统控制实验,为其可行性和适用性提供依据.
2 Legendre多项式
Legendre公式定义如下:

式中:n为非负实数,设方程幂级数解:y=y1+y2.

当n为非负整数时,y1和y2在区间[-1,1]内为式(2)的解.其中y2退化为n阶Legendre多项式,成为式(2)在区间[-1,1]的有界解,通过选定最高次幂系数an,可得到n阶Legendre多项式[9].
当n=0,1,2,3,…时,可得到迭代的Legendre多项 式:P0(x)=1;P1(x)=x;P2(x)=;依次类推,理论上可迭代到任意Pn(x).

Legendre多项式有一个重要的正交特性如式(6)所示:

使用传统的最小二乘法拟合曲线函数可得:
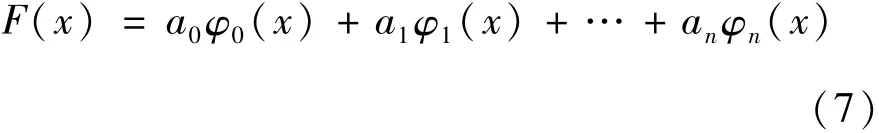
通常要考虑加权平方和:
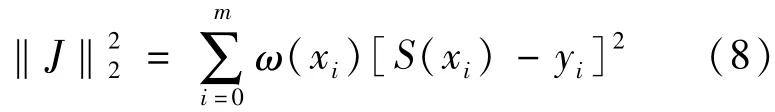
式中:ω(xi)≥0,为[a,b]上的权函数,表示不同点(xi,f(xi))处的数据比重不同.权函数能反映出板形缺陷的真实曲线形状,但需要更多的高次项来确定逼近阶数n的大小,函数的系数求解精度和唯一性也不确定,易造成控制精度不高.具有正交性的多项式能很好地解决这些问题,因此在安徽楚江670 mm铜精轧机的板形控制中,为满足板形残余应力的约束条件(B为板宽,F(x)为沿板宽的残余应力),采用Legendre多项式Pk(x)的线性组合来进行最小二乘拟合,通过Legendre级数来逼近一个函数,并根据式(5)进行递推,计算出系数a*k:
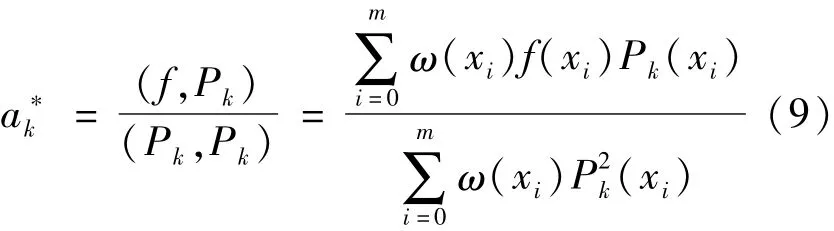
逐步把a*kPk(x)累加到F(x)中去,得到所需拟合曲线:
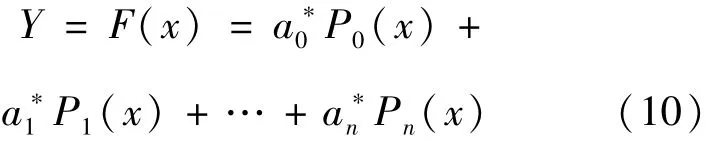
式中,n通过预设给定或在计算中根据误差来确定.使用该方法编程无需求解方程组,在逼近次数增加一次时,利用递推公式增加循环数即可得到结果.
从以上迭代推导式可看出,Legendre多项式Pk(x)同时存在一次项和三次项.目前的轧机设备中大多无对应三次项的调整机构,常用的Legendre多项式会带来与期望结果相反的调整策略.为提高板形模式识别精度,本文采用Legendre多项式优化算法对缺陷识别算法进行改进.
3 Legendre多项式的优化及仿真
经前述分析可知,Legendre多项式给定的参数不适合多变的轧制情况,因此采用正交多项式,建立精确的板形测量值及求解的误差平方和最小等约束条件,进行Matlab仿真来确定多项式参数,过程如下:

给定F(x)=λ(0)+αt,
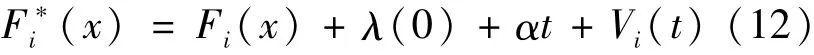
式中:F(x)为板形基函数;Vi(t)为随机噪声.

将采集的安徽楚江650 mm铜精轧机板形实测数据带入上式中,式中选择一次、四次和八次多项式等归一化方程来描述板形基模式,如式(15)~(20)所示:

由以上公式组合成线性多项式:

式中,a*1,a*4,a*8为板形的特征系数.
通过Matlab软件得到仿真结果,如图1所示.相应的模型参数和板形特征仿真结果见表1.

图1 6种Legendre多项式板形缺陷基模式Fig.1 Six Legendre polynomial flat defect base modes
从表1中识别结果的均方差量值上可以看出,在Legendre多项式中对三次项进行简化,优化模型参数得到的板形识别函数能够改善Legendre多项式对板形控制效果的影响,回归结果更接近实际情况,且操作运算简单直观,计算时间短.因此,采用这种板形识别方法能够计算出有效的板形特征值.

表1 板形特征值仿真结果Table 1 Simulation results of flatness eigenvalues
4 650 mm铜精轧机板形控制
在安徽楚江科技公司的650 mm铜精轧机上对本文算法进行了验证,该轧机产品有黄铜板带、紫铜板带和磷铜板带,产品参数如表2所示,设备参数如表3所列(表中,I为板形单位,板形单位是指板带材横向上最长与最短纵条之间的相对长度差).

表2 650 mm轧机产品参数Table 2 650 mm rolling mill product parameters mm

表3 650 mm轧机设备参数Table 3 650 mm rolling mill equipment parameters
板形测量仪采用空气轴承式板形辊,测量区宽度为9×26+4×52+9×26=676 mm,传感器分布为9+4+9,带材包角为16°.核心控制系统为西门子S7-400,CPU为416-2XN05-0AB0,指令执行时间为0.03μs.控制系统和板形测量辊之间使用Profibus通讯协议,模拟量和数字量通过以太网从轧机传动系统读取.控制程序分为板形测量信号处理模块、板形控制模块(含板形缺陷识别)、逻辑操作模块和通讯处理模块4个模块.
图2为板形控制系统HMI图,其中平直度分布显示实时板带材横向形状,工作辊冷却量为冷却喷嘴实时控制量.

图2 650 mm板形控制系统HMIFig.2 650 mm shape control system HMI
经650 mm轧机多品种多道次轧制,本文优化算法能够识别更多的板形缺陷,控制精度得到了很大提高.对比图3~4所示的现场板形误差值和板形误差二维曲线可看出,当不投入本优化识别算法时,板形平均误差在±8 I左右;而使用所示优化算法后,板形平均误差在±6 I左右,表明改进的识别算法能提高板形控制精度.
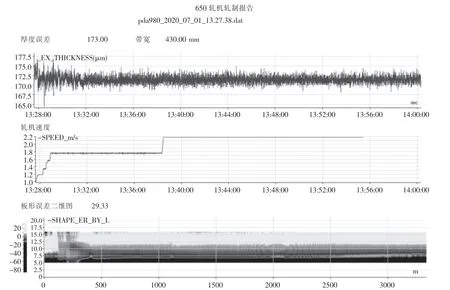
图3 未经优化识别的板形精度二维图Fig.3 2D chart of shape accuracy without optimization identification

图4 经优化识别的板形精度二维图Fig.4 2D chart of shape accuracy with optimized identification
5 结 论
(1)本文提出一种基于Legendre多项式的板形识别优化算法.该优化算法运算简单直观,计算时间短,能有效得到板形特征值,既弥补了常用的最小二乘法进行板形识别的缺陷,又避免了Legendre多项式对轧机三次项调整机构的要求,使板形识别模型更接近真实板形测量形状,符合实际生产的工艺要求.
(2)经某厂650 mm铜板带轧机验证,使用该优化算法后,板形平均误差从±8 I减小到±6 I,精度提高了10%左右.
