水泥改良黄土路基动力稳定性评价参数试验研究

2019-04-19张沛云马学宁

水文地质工程地质 2019年2期

张沛云，马学宁

(兰州交通大学土木工程学院，甘肃兰州 730070)

随着高速铁路的高速发展，在黄土地区修建高速铁路遇到的问题越来越多，由于黄土天然的软弱性，不能直接作为路基填料，而依靠外运合格填料既不经济也不合理。因此将黄土进行改良后使用的技术得到迅速发展，基床底层填料改良已成为高速铁路路基设计的重要内容[1]。

在高速铁路无砟轨道路基设计中，由于列车行驶速度高，其对沉降的要求也更为严格，因此，需充分考虑列车荷载下路基的动态响应，来确保路基的长期动力稳定性满足要求。过去我国普速铁路通常采用临界动应力法来对路基的动力稳定性进行研究[2-3]，该方法是以路基填料的动强度作为控制指标，相关学者针对不同的路基填料进行了大量的研究。梅慧浩等[4]对基床粗粒土填料进行了动三轴试验，得出不同动力行为之间临界应力的表达式，建立了累积塑性应变预测模型。段俊彪[5]从临界动应力及应力应变关系出发，对水泥土和石灰土动力特性的不同和变化规律进行了深入的研究。由于该方法考虑因素不全面，而高速铁路对沉降的要求更为重要，往往当路基填料受力小于其临界动应力，未发生强度破坏前，其累积塑性变形可能已经大于容许沉降。因此，使用临界动应力法评价高速铁路路基的动力稳定性存在问题。胡一峰[6-8]在总结前人研究成果的基础上，提出了动剪应变法来评价高速铁路路基的动力稳定性。该方法是一种更为系统、全面的动力稳定性评价方法。而使用动剪应变法评价高速铁路路基动力稳定性需要两个基本参数：短时及疲劳动剪应变门槛。Vucetic[9]通过剪应变控制式共振柱试验，在大量试验结果的基础上，得到各类土的动剪应变门槛统计值；Youd[10]、Silver等[11]通过动三轴试验得到密实度、固结比等因素对剪切应变门槛的影响；刘晓红[12-13]通过应力控制式动三轴仪对红黏土的动剪应变门槛进行了测定，并通过动剪应变法对无砟轨道路堑基床换填厚度进行了分析；谢琦峰等[14]等通过动三轴实验研究了黏质粉土累积塑性变形受围压、动应力、排水条件等的影响规律。

目前，还未见有关水泥改良黄土动剪应变门槛的研究报道，也未见有针对其作为高速铁路路基基床底层填料时的动力稳定性研究报道。这种改良填料究竟能否满足高速铁路基床对长期动力稳定性的要求，需要通过动剪应变法进行评价。而评价体系关键参数(短时及疲劳动剪应变门槛)的试验过程较为复杂，实现起来较为困难，尤其疲劳动剪应变门槛试验所需时间长、工作量大。故本文通过短时及疲劳动三轴试验，研究不同水泥掺量、围压及固结比条件下水泥改良黄土的短时及疲劳动剪应变门槛的变化规律，并探讨了相对应的短时及疲劳动剪应变门槛之间的量值关系，以期通过相对较为方便的短时动三轴试验得到疲劳动剪应变门槛，为实际工程中相关问题提供参考和思路。

1 基本物理力学指标

选取兰州九州台黄土为研究对象，通过室内试验测得其液限为28.5%，塑限15.3%，塑性指数为13.2，最优含水率为14.8%，最大干密度为1.86 g/cm3，通过颗分试验，得到其粒径范围大于0.05的颗粒占41.2%，粒径位于0.05～0.01 mm的占53%，0.01～0.005 mm的为3.8%，而小于0.005 mm的占2%。

采用甘肃祁连山42.5#普通硅酸盐水泥按照3种配合比(η=3%，5%，7%)对黄土进行改良，通过击实试验得到不同水泥掺量的改良黄土最大干密度及最优含水率如表1所示。

表1 水泥改良土击实试验结果Table 1 Experimental results of modified loess compaction

2 短时及疲劳动三轴试验

2.1 试验方案

图1 轴向应力和应变随时间的变化曲线Fig.1 Axial stress and strain versus time

2.2 短时动三轴试验及短时动剪应变门槛的确定

2.2.1试验过程

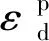
2.2.2短时动剪应变门槛的确定方法

以围压σ3=10 kPa、Kc=1的5%水泥改良黄土试验结果为例，具体说明短时动剪应变门槛的确定方法。

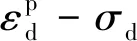
采用6061铝合金和AZ31B镁合金作为试验材料，试板尺寸为300 mm×70 mm×6 mm，其质量分数分别见表1和表2。试验前先用砂纸将镁板和铝板打磨干净，除去表面氧化膜，再分别用丙酮和酒精擦拭待焊部件油污部位。然后用夹具将对接的两板固定，采用根部直径为6.2 mm，端部直径为4.3 mm，轴肩直径15 mm，长度为5.7 mm，带有螺纹的锥形搅拌针进行镁/铝异种金属的搅拌摩擦焊试验。利用扫描电镜观察断口形貌和能谱分析并用XRD对断口物相进行分析。

图曲线Fig.2 Vertical plastic strain versus dynamic stress

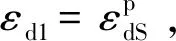
2.3 疲劳动三轴试验及疲劳动剪应变门槛的确定

2.3.1实验过程

选择CU模块进行饱和与固结。试样稳定后关闭排水阀，施加第一级轴向动应力σd1，振动次数取至少10 000次，振动过程中记录轴向动应变幅值εd1；振动完成后，将第一级动应力σd1卸除，同时打开排水阀门。同样，将试样在固结应力作用下静置一段时间；关闭排水阀，施加下一级轴向动应力直至试样破坏。

2.3.2疲劳动剪应变门槛的确定方法

依据试验结果，计算动模量Ed=σd/εd，依据Ed-σd曲线确定动模量门槛EdL，进而得到疲劳动剪应变门槛γtvL。以围压σ3=60 kPa，Kc=1的5%的水泥改良黄土试验结果为例作具体说明。

(1)每1 000次振动计算1个动模量，每一动应力水平下取10个数据点，取平均值作为此级应力水平σd下的动模量Ed，绘制Ed-σd曲线(图3)。

图3 Ed-σd曲线Fig.3 Dynamic modulus Ed versus dynamic σd

(2)由图3可知，随着动应力σd的增加，动模量Ed呈现出先增大后减小的趋势。在加载初期，动应力较小时，随着动应力的增大，试样逐渐被压密，则Ed逐渐增大；当动应力达到某一值时，Ed达到峰值；随后，动应力继续增大，Ed开始逐渐减小，可知土样受到较大的扰动，承载能力显著降低，甚至发生破坏。

(4)与短时动剪应变门槛的确定方法相同，设试样大主应变εd1=εdL，小主应变εd3=-0.5εdL，以[(εd1+εd3)/2,0]为圆心，以(εd1-εd3)/2为半径绘制应变莫尔圆，该莫尔圆的半径(εd1-εd3)/2即为最大剪应变，也就是疲劳动剪应变门槛γtvL。

3 试验结果分析

3.1 短时动剪应变门槛

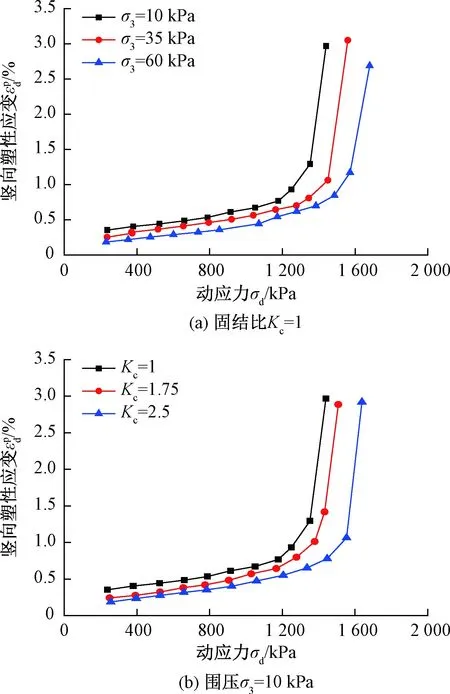
图曲线

根据短时动剪应变门槛及短时动应力门槛确定方法，得到不同试验条件下的结果如图5所示。由图5可知，短时动剪应变门槛γtvS及短时门槛动应力σdS受水泥掺量、围压及固结比的影响显著，均随着3种影响因素的增大呈近似线性增大。

图5 水泥掺量、围压及固结比对短时动剪应变门槛和短时动应力门槛的影响Fig.5 Effect of η, σ3 and Kc on the short-term dynamic shear strain and dynamic stress threshold

以水泥掺量为5%时围压及固结比对短时动剪应变及动应力门槛的影响为例。当固结比Kc=1时，围压σ3从10 kPa增加到60 kPa，短时动剪应变门槛γtvS从6.37×10-3增加到7.58×10-3，增幅为18.9%；而短时动应力门槛σds从1 214 kPa增加到1 529 kPa，增加了25.9%。当σ3=10 kPa时，Kc从1增加到2.5，γtvS从6.37×10-3增加到7.07×10-3，增幅为10.8%；σds从1 214 kPa增加到1 470 kPa，增加了21%。而当σ3=10 kPa，Kc=1时，水泥掺量从3%增加到7%，则γtvS从3.93×10-3增加到7.97×10-3，增大了102.8%，而σds从823 kPa增大到1 638 kPa，增大了99%。

可见在影响水泥改良黄土短时动剪应变门槛的3种因素中，水泥掺量的变化对其影响最大，即其受水泥掺量的影响敏感性最高，围压的影响次之，固结比的影响最小。对短时动应力门槛的影响与之类似。

鉴于上述试验过程较为复杂，对试验仪器的要求较高，为更好地应用于实际中，将不同试验条件下的试验结果进行三元线性回归分析，则水泥改良黄土的短时动剪应变门槛及动应力门槛的经验估算公式如下：

γtvS=(1 003.64η+0.191σ3+3.773Kc+5.61)×10-4

R=0.982 8 (1)

σdS=16 109.34η+5.556σ3+177.51Kc+226.18

R=0.973 8 (2)

3.2 疲劳动剪应变门槛

通过前述确定疲劳动剪应变门槛的方法，得到不同水泥掺量、围压及固结比时水泥改良黄土Ed-σd曲线，以水泥掺量为5%时的部分试验结果为例(图6)。由图6可见，随着动应力的增大，水泥改良黄土的动模量呈现出先增大后减小的趋势，动应力水平较低时，随着土体的逐渐压密，其动模量逐渐增大，当动应力增大到一定值时，土体塑性变形急剧增大，逐渐破坏，故在加载后期动模量逐渐减小。且不同试验工况下动模量随动应力的变化趋势基本相同，即在同一动应力水平下，随围压和固结比的增大而增加，相应的动模量门槛及动应力门槛变化类似。

图6 Ed-σd曲线Fig.6 Dynamic modulus Ed versus dynamic σd

不同试验条件下疲劳动剪应变门槛及疲劳门槛动应力的结果如图7所示。可见，疲劳门槛动应力随水泥掺量、围压及固结比的增大逐渐增大。

图7 水泥掺量、围压及固结比对疲劳动剪应变和疲劳动应力门槛的影响Fig.7 Effect of η, σ3 and Kc on the fatigue dynamic shear strain and dynamic stress threshold

以水泥掺量为5%的情况为例。当Kc=1，σ3从10 kPa增加到60 kPa，γtvL从1.9×10-3增加到2.47×10-3，增幅为30%；而σdL从516 kPa增加到800 kPa，增量为55%。当σ3=10 kPa，Kc从1增加到2.5时，γtvL从1.9×10-3增加到2.17×10-3，增幅为14.2%；相应的σdL从516 kPa增加到660 kPa，增加了27.9%。而当σ3=10 kPa，Kc=1时，水泥掺量从3%增加到7%，则γtvL从1.14增大到2.27，增大90.3%；σdL从350 kPa增大到750 kPa，增加114.3%。

同样可见，水泥掺量对疲劳动剪应变门槛及疲劳动应力门槛的影响最大，围压的影响次之，固结比的影响最小。

考虑3种因素对疲劳动剪应变门槛的影响，在选择路基填料时，首先应合理选择水泥掺量，其次考虑围压及固结比的影响，在路基设计及动力稳定性评价时，疲劳动剪应变门槛的取值一定要具体考虑各路段的工程地质条件，如基床土物理状态及实际受力状况等，以达到安全经济的目的。

经回归分析可得到水泥改良黄土疲劳动剪应变门槛及疲劳动应力门槛随水泥掺量、围压及固结比的经验估算公式如下：

γtvL=(3 177.78η+0.847σ3+18.07Kc-1.82)×10-5

R=0.984 4 (3)

σdL=7 000.3η+5.498σ3+132.88Kc-23.279

R=0.967 8 (4)

公式(1)～(4)为水泥改良黄土填料短时、长期动力稳定性评价参数的经验估算公式，相关系数较高，可为高速铁路水泥改良黄土基床底层的动力稳定性研究提供一定的参考。但结果只在一定范围内适用(3%≤η≤7%，10≤σ3≤60，1≤Kc≤2.5)，实际应用时需注意其取值范围。

3.3 动力相关性研究

鉴于采用动剪应变法来评价路基长期动力稳定性，其关键参数疲劳动剪应变门槛的确定需通过疲劳动三轴试验来获取，而该试验耗时太长、工作量大，为了能更好地为实际工程提供参考，从短时动三轴试验数据出发，通过对比分析，找到短时与疲劳动剪应变门槛之间的量值关系，实现通过短时动三轴试验来获取疲劳参数的方法。

设疲劳动剪应变门槛与短时动剪应变门槛的比值为K=γtvL/γtvS，则各试验条件下水泥改良黄土填料的K值如表2所示。

表2 短时及疲劳动剪应变门槛的关系Table 2 Relationship between the short-term and fatiguedynamic shear strain threshold

由表2可知，K值在0.29～0.34之间变化，即γtvL=(0.29～0.34)γtvS，变化范围不大。由前述可知，随着水泥掺量、围压及固结比的增大，短时及疲劳动剪应变门槛均呈近似线性增大的趋势，故K值的变化情况是合理的。实际工程中可首先通过相对简单的短时动三轴试验获得短时动剪应变门槛，乘以K的比例系数，近似得到疲劳动剪应变门槛。从而消除了疲劳动剪应变工作量大、试验复杂且难以实现的弊端，为今后该方面的研究提供了新的思路与方法。