散货船自由浮态计算简化方法

刘 春 雷， 尹 勇， 孙 霄 峰， 张 秀 凤， 神 和 龙

( 大连海事大学 航海动态仿真和控制交通行业重点实验室， 辽宁 大连 116026 )

散货船自由浮态计算简化方法

刘 春 雷， 尹 勇*， 孙 霄 峰， 张 秀 凤， 神 和 龙

( 大连海事大学 航海动态仿真和控制交通行业重点实验室， 辽宁 大连 116026 )

根据散货船特点探讨了一种面向工程应用的船舶自由浮态计算简化方法．在矩阵法的基础上，将7个水线面要素简化到4个，简化雅克比矩阵求解．采用全选主元高斯消去法求解线性方程组，以船舶浮态平衡方程组作为迭代终止条件，保证计算精度．以散货船“DOLCE VITA”及“RUI AN CHENG”为例进行了实例计算，对20个压载舱进行了20万次随机装载实验，验证了算法在有横倾下的收敛性和稳定性；对5个货舱进行了20万次随机装载实验，验证了算法在有纵倾下的收敛性和稳定性；对典型载况进行计算，和装载手册给定值相比，吃水差误差都在0.01 m以下．结果表明：该算法只需计算任意倾斜水线面下的排水体积和浮心坐标，计算量较小，程序实现简单，实时性、鲁棒性较好，具有一定的工程实用价值．

船舶工程；自由浮态；散货船；配载仪；吃水差

0 引 言

船舶浮态计算是指计算船舯吃水Tm、横倾角θ及纵倾角φ，在船体坐标系下多采用艏吃水Tf、艉吃水Ta及横倾角θ表示．船舶浮态计算是保障船舶航行安全的重要前提，也是船舶稳性计算、船舶剪力和弯矩计算、自动配载及装卸货过程优化的基础．

目前船舶浮态计算方法大体可分为4类：第1类是依靠船舶静水力资料计算的常规法[1-2]；第2类是采用牛顿迭代的矩阵法[3-6]；第3类计算方法可归结为优化法，主要有文献[7-8]提出的非线性规划法及文献[9-11]提出的遗传算法；第4类是有限元法，通过有限元分析计算船舶浮态[12-14]．

但是这4类算法存在一些不足：第1类常规法以船舶静水力数据为基础，将纵倾和横倾分开计算，适用于小纵倾计算，纵倾和横倾较大时误差会增大；第2类矩阵法在每一次迭代计算时都要计算包含水线面面积、漂心、惯性矩、排水体积及浮心等多项要素的雅克比矩阵，需实时计算船舶倾斜水线面，计算量较大，程序处理困难；第3类优化法只需要计算排水体积和浮心，避免了雅克比矩阵的计算，减少了计算量，但是迭代次数较多，收敛速度有时比较缓慢，影响程序实时性，不太适用于工程应用；第4类算法采用有限元法，需建立船舶有限元模型，计算量大，实时性不好．

针对以上不足，本文根据散货船方形系数较大的特点，探讨一种面向工程应用的浮态迭代算法，在求解雅克比矩阵时，用过船艉吃水处且平行于基平面的水线面代替倾斜水线面在基平面的投影面，将求解雅克比矩阵时的7个水线面要素简化到4个，简化雅克比矩阵求解，程序只需计算任意倾斜水线面下的排水体积及浮心坐标，以使编程实现简单，稳定可靠．

1 船舶自由浮态方程组求解

本文采用固定在船上的Oxyz坐标系统：原点O为基平面、中站面和中线面的交点．x轴为基平面和中线面的交线，指向船艏为正．y轴是基平面和中站面的交线，指向右舷为正．z轴是中线面和中站面的交线，向上为正．船舶任意浮态平衡方程组为[5]

(1)

式中：ρ为海水密度；V为排水体积；Δ为船舶总装载量；xb、yb、zb为船舶浮心纵向、横向及垂向坐标；xg、yg、zg为船舶重心纵向、横向及垂向坐标；θ为船舶横倾角；φ为船舶纵倾角．

在求解时，一般通过牛顿迭代求解非线性方程组[5]，其雅克比矩阵为

(2)

在求解雅克比矩阵时，其难点是7个水线面要素S、xf、yf、zf、Ixf、Iyf、Ixyf的求解，需要倾斜水线面和船体实时求交计算水线面的轮廓数据，文献[6]提出一种获得水线面轮廓的排序方法．本文根据散货船的特点提出一种简化方法，将7个水线面要素简化到4个，且不需要实时计算．如图1所示，散货船的方形系数较大，可用过船艉吃水Ta处的平行于基平面的水线面Aw1近似代替倾斜水线面在基平面的投影面Aw．

根据水平水线面S1特点可得到如下性质：yf=0，Ixy=0，zf=Tm-dtanφ≈Tm，d为漂心纵向坐标距船舯的距离，另外根据平行移轴原理则可得到Ix、Iy、Ixy与Ixf、Iyf、Ixyf的对应转换关系(Ix、Iy、Ixy分别为水线面对x、y轴的惯性矩和惯性积)：

(3)

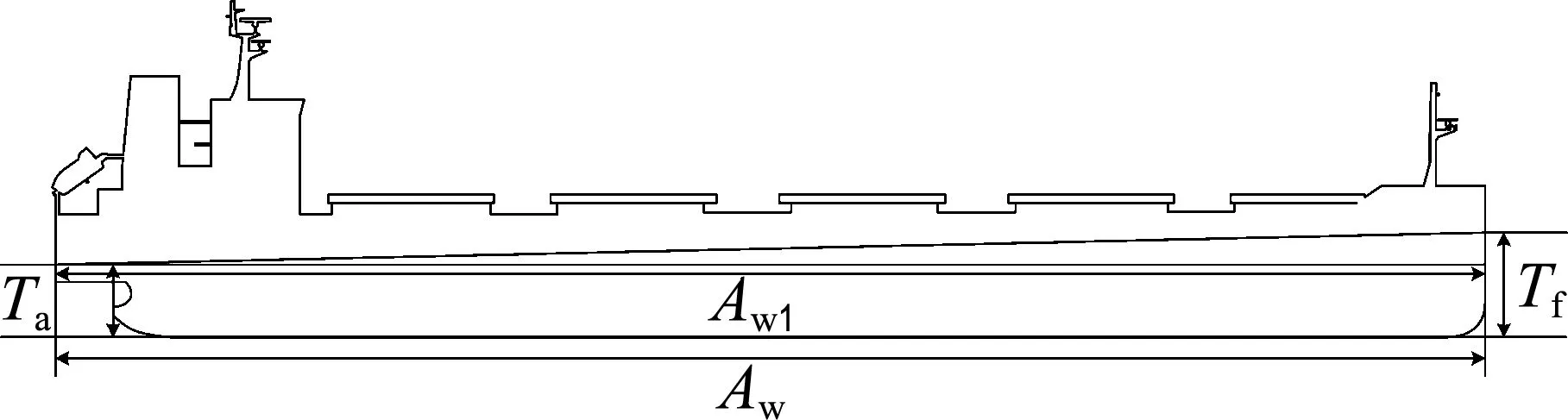
图1 水线面投影

则原雅克比矩阵可简化为

(4)

由式(4)可知，求解方程组只需要计算4个水线面要素S、xf、Ix及Iyf．在编写程序时可离线计算出各个吃水下的水线面参数值，建立离线数据库，根据船艉吃水进行离线插值，提高程序计算效率．在建立离线水线面数据库时可由船舶设计部门提供的船舶静水力表获得，也可采用格林公式进行计算，计算公式如式(5)所示：

(5)

其中My是水线面对y轴的静矩．

采用全选主元高斯消去法求解三元一次线性方程组，以船舶任意浮态平衡条件作为迭代终止判断条件，当满足船舶平衡条件时输出浮态计算结果：

(6)

式中：ε1、ε2、ε3为迭代精度控制，本文取ε1=5，ε2=0.001，ε3=0.001．

2 程序设计

首先采用常规法计算船舶浮态初始值，然后采用迭代法进行迭代，直到满足船舶浮态平衡条件，程序设计流程图如图2所示，其具体步骤如下：

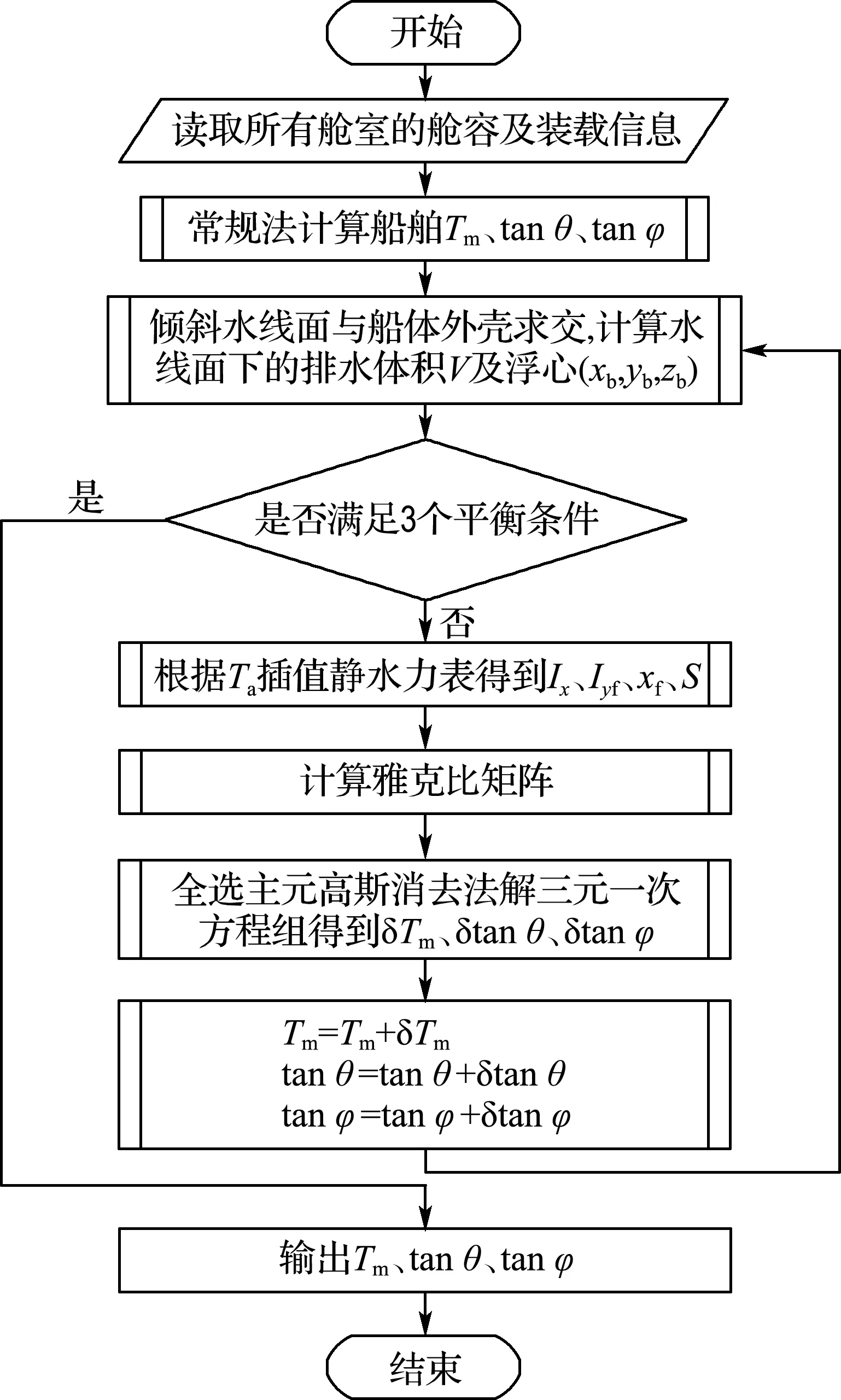
图2 程序设计流程图

步骤1 计算船舶总装载量Δ及重心坐标(xg,yg,zg)．

步骤2 常规法计算船舶Tm、tanθ、tanφ．

步骤3 计算船舶倾斜水线面方程xtanφ+ytanθ-z+Tm=0，倾斜水线面和船舶外壳求交计算水线面下排水体积V和浮心坐标(xb,yb,zb)．

步骤4 根据式(6)判断是否满足平衡条件，即判断总装载量和排水量是否相等、重心和浮心是否在同一条垂线上,如果不满足，则转步骤6．

步骤5 浮态程序计算结束，输出当前浮态结果Tm、tanθ、tanφ．

步骤6 根据Ta插值静水力表计算Ix、Iyf、xf、S．

步骤7 计算雅克比矩阵．

步骤8 全选主元高斯消去法解三元一次方程组得到δTm、δtanθ和δtanφ．

步骤9 计算船舶Tm、tanθ、tanφ：

(7)

转步骤3．

3 算 例

本文以38 000 t散货船“DOLCE VITA”和“RUI AN CHENG”为例进行算法收敛性和准确性测试：(1)对其20个压载舱进行20万次随机装载实验测试算法在有横倾情况下的收敛性和稳定性；(2)对其5个货舱进行20万次随机装载实验测试算法在船舶有吃水差下的收敛性和稳定性；(3)对几种典型载况进行计算，和装载手册给定值相比较验证算法准确性．

算例1 20个压载舱20万次随机装载实验

在初始装载状况为空载的情况下进行了20万次随机装载实验，以每个压载舱的最大舱容为限制，在20个压载舱随机产生装货量进行浮态计算．计算结果如图3所示，船舶横倾角计算结果的分布范围从左倾12.160°到右倾12.856°，最大迭代次数为5次，最小迭代次数为1次，全部20万次装载方案的平均迭代次数为2.29次．1次迭代即可收敛的载况为10 737个，2、3、4、5次迭代收敛的载况分别为124 402、60 813、4 013及35个，迭代失败的次数为0．

图4所示为各横倾角下的平均迭代次数，从图中可看出随着横倾角绝对值的减小，迭代次数逐渐减少：船舶横倾角位于-13°～-12°时平均迭代次数为5次；横倾角位于0°～1°时平均迭代次数为1.9次；横倾角位于11°～12°时平均迭代次数为5次．

图3 各迭代次数下的载况数(横倾)

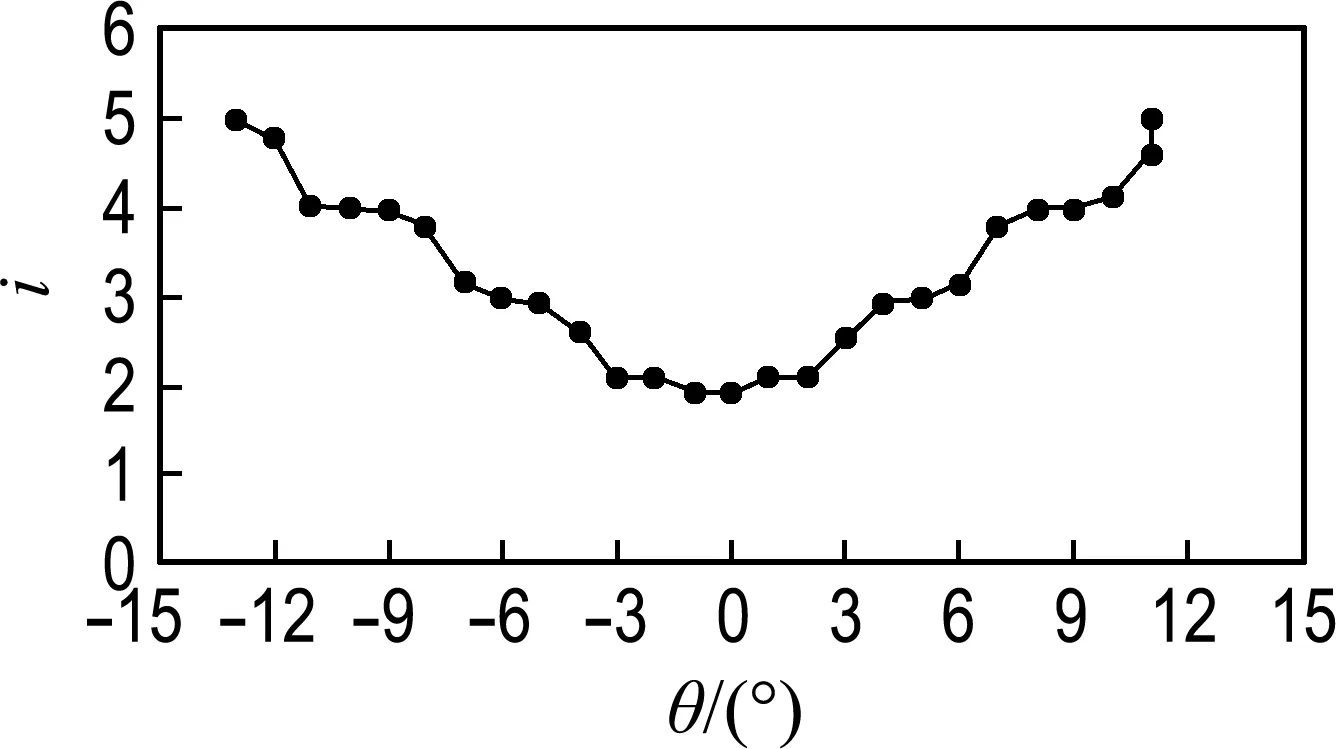
图4 各横倾角下的平均迭代次数

从实验结果可以看出算法在横倾角较小时一般需要1～2次迭代即可收敛，当横倾角较大时一般不超过5次迭代即可收敛，验证了算法在船舶存在横倾时的收敛性和稳定性．

算例2 5个货舱20万次随机装载实验

在初始装载状况为空载的情况下进行了20万次随机装载实验，以每个货舱的最大舱容为限制，在5个货舱随机产生装货量进行浮态计算．计算结果如图5所示，船舶吃水差计算结果从-13.040 m到13.508 m，最大迭代次数为6次，最小迭代次数为1次，全部20万次装载方案的平均迭代次数为1.74次．1次迭代即可收敛的载况为89 949个，2、3、4、5、6次迭代收敛的载况分别为80 759、22 143、5 430、1 567及152个，迭代失败的次数为0．

图6所示为各吃水差下的平均迭代次数，从图中可看出随着吃水差绝对值的减小，迭代次数逐渐减小：船舶吃水差位于-14～-13 m时平均迭代次数为4次；吃水差位于0～1 m时平均迭代次数为1.27次；吃水差位于12～13 m时平均迭代次数为5次．

图5 各迭代次数下的载况数(纵倾)

图6 各吃水差下平均迭代次数

从实验结果可以看出算法在吃水差较小时一般需要1～2次迭代即可收敛，当吃水差较大时一般不超过6次迭代即可收敛，验证了算法在船舶存在纵倾时的收敛性和稳定性．

算例3 算法准确性验证

为验证算法准确性，本文对 “DOLCE VITA”4种典型载况进行了实例计算，如表1所示．表2为“RUI AN CHENG”8种典型载况的浮态计算结果．

分析表1、2中数据可知：(1)吃水差误差都在0.010 m以下，最大误差为0.009 m,可见采用本文方法计算的船舶浮态计算结果和装载手册给定值误差较小，具有较高的计算精度．(2)船舶空船载况下，船舶吃水差较大，本文方法需要进行4次迭代，其他载况基本需要1次迭代即可获得较精确的结果．

表1 散货船“DOLCE VITA”浮态计算结果

表2 散货船“RUI AN CHENG”浮态计算结果

可见，本文算法以船舶浮态方程组作为迭代终止条件，只有满足船舶平衡条件时才输出计算结果，保证了计算精度，和装载手册给定值相比误差较小，验证了算法的可行性与准确性．

基于文中所述浮态算法，大连海事大学航海研究所自主研发出一套基于STL模型散货船装载计算机程序，如图7所示，目前该软件正在申请CCS及DNV船级社的型式认可．

图7 散货船配载仪

4 结 论

(1)针对散货船的特点，在矩阵法的基础上探讨了一种面向工程应用的船舶浮态迭代算法．相比于常规法，本文算法适用于任意浮态；相比于矩阵法减少了水线面面积、漂心、惯性矩等要素的实时求解，减少了计算量；相比于优化法及有限元法减少了迭代次数．

(2)算法以船舶浮态平衡方程组作为迭代终止条件，保证了计算精度．

(3)算法简单，容易编程实现，依赖于离线静水力表，只需要计算出任意倾斜水线面下的排水体积和浮心，具有实时性、鲁棒性及准确性，工程实用价值较高．

本文算法已经成功应用在自主研发的散货船装载计算机系统中，计算船型覆盖了38 000、64 000 及250 000 t级别的主流散货船型，未来将在此基础上研究船舶自动配载、货物装载过程中优化等方面内容．

[1] 段兴锋,任鸿翔,东 昉. 纵倾状态船舶浮态的研究与计算 [J]. 中国航海, 2015, 38(1):54-57.

DUAN Xingfeng, REN Hongxiang, DONG Fang. Calculation of floating condition of a longitudinal inclined ship [J]. Navigation of China, 2015, 38(1):54-57. (in Chinese)

[2] 刘春雷,尹 勇,孙霄峰,等. 船舶浮态计算的一种修正方法[J]. 大连海事大学学报, 2014, 40(4):1-6.

LIU Chunlei, YIN Yong, SUN Xiaofeng,etal. A modified method to ship floating calculation [J]. Journal of Dalian Maritime University, 2014, 40(4):1-6. (in Chinese)

[3] CHEN Jing, LIN Yan, HUO Junzhou,etal. Optimization of ship′s subdivision arrangement for offshore sequential ballast water exchange using a non-dominated sorting genetic algorithm [J]. Ocean Engineering, 2010, 37(11/12):978-988.

[4] CHEN Jing, LIN Yan, HUO Junzhou,etal. Optimal ballast water exchange sequence design using symmetrical multitank strategy [J]. Journal of Marine Science and Technology, 2010, 15(3):280-293.

[5] 赵晓非,林 焰. 关于解船舶浮态问题的矩阵方法[J]. 中国造船, 1985(3):55-64.

ZHAO Xiaofei, LIN Yan. Matrix methods for solving ship floating state problem [J]. Shipbuilding of China, 1985(3):55-64. (in Chinese)

[6] 林 焰,李铁骊,纪卓尚. 破损船舶自由浮态计算[J]. 大连理工大学学报, 2001, 41(1):85-89.

LIN Yan, LI Tieli, JI Zhuoshang. Ship damage floating calculation [J]. Journal of Dalian University of Technology, 2001, 41(1):85-89. (in Chinese)

[7] 马 坤,张明霞,纪卓尚. 基于非线性规划法的船舶浮态计算[J]. 大连理工大学学报, 2003, 43(3):329-331.

MA Kun, ZHANG Mingxia, JI Zhuoshang. Ship floating calculation based on nonlinear programming [J]. Journal of Dalian University of Technology, 2003, 43(3):329-331. (in Chinese)

[8] 孙承猛,刘寅东. 船舶浮态计算的一种优化方法[J]. 大连海事大学学报, 2006, 32(2):39-41.

SUN Chengmeng, LIU Yindong. Optimization method for ship′s floating condition calculation [J]. Journal of Dalian Maritime University, 2006, 32(2):39-41. (in Chinese)

[9] 陆丛红,林 焰,纪卓尚. 遗传算法在船舶自由浮态计算中的应用[J]. 上海交通大学学报, 2005, 39(5):701-705,710.

LU Conghong, LIN Yan, JI Zhuoshang. Application of genetic algorithm in ship free floatation calculation [J]. Journal of Shanghai Jiaotong University, 2005, 39(5):701-705, 710. (in Chinese)

[10] LU Conghong, LIN Yan, JI Zhuoshang. Free trim calculation using genetic algorithm based on NURBS shipform [J]. International Shipbuilding Progress, 2007, 54(1):45-62.

[11] LU Conghong, LIN Yan, JI Zhuoshang. An algorithm for plane-surface intersection and its application to shipbuilding [J]. Ship Technology Research, 2005, 52(3):103-106.

[12] CALABRESE F, MANCARELLA L, ZIZZARI A A,etal. A multidisciplinary method for evaluating ship stability [J]. Journal of Shipping and Ocean Engineering, 2012, 2(6):321-326.

[13] CALABRESE F, CATALDO M, DE PASCALIS A,etal. A method for evaluating the ship equilibrium point using 3D meshes developed for embedded device [C] // MTS/IEEE OCEANS 2015-Genova: Discovering Sustainable Ocean Energy for a New World. Piscataway:IEEE, 2015:7271763.

[14] AZCUETA R. Computation of turbulent free-surface flows around ships and floating bodies [J]. Ship Technology Research, 2002, 49(2):46-69.

Simplified method of bulk carrier′s free floatation calculation

LIU Chunlei, YIN Yong*, SUN Xiaofeng, ZHANG Xiufeng, SHEN Helong

( Key Laboratory of Marine Simulation and Control Ministry of Communication, Dalian Maritime University, Dalian 116026, China )

According to the characteristics of bulk carrier, a simplified method of ship free floatation calculation for engineering application is studied. Based on matrix method, 7 waterline plane elements are reduced to 4, and the solution of Jacobi matrix is simplified. Complete Gaussian pivoting elimination method is adopted to solve the linear equations. In order to ensure the accuracy of the calculation, the floating state balance equations are used as the iteration stop conditions. Bulk carrier “DOLCE VITA” and “RUI AN CHENG” are taken as examples, 200 000 random loading experiments are carried out on 20 ballast tanks to verify the convergence and robustness of the algorithm in heeling condition. 200 000 random loading experiments are carried out on 5 cargo holds to verify the convergence and robustness of the algorithm in trim condition. Typical load conditions are calculated, and compared with the given value in the loading manual the trim error is less than 0.01 m. The calculation results show that in this algorithm the calculating amount is decreased because only displacement volume under any tilt waterline plane and center of buoyancy need to be computed, the calculation amount is small, the program is very simple, real-time, robust and has a certain engineering application value.

ship engineering; free floatation; bulk carrier; loading computer; trim

1000-8608(2017)01-0055-06

2016-05-21；

2016-11-24．

“八六三”国家高技术研究发展计划资助项目(2015AA016404)；海洋公益性行业科研专项(201505017-4)；中央高校基本科研业务费专项资金资助项目(3132016310).

刘春雷(1987-)，男，博士生，E-mail:18940930042@163.com；尹 勇*(1969-)，男，教授，E-mail:bushyin@163.com.

U661.21

A

10.7511/dllgxb201701008