船舶动力定位反步逆最优控制

徐 海 祥， 瞿 洋， 余 文 曌1,

( 1.武汉理工大学 高性能船舶技术教育部重点实验室, 湖北 武汉 430063；2.武汉理工大学 交通学院, 湖北 武汉 430063 )

船舶动力定位反步逆最优控制

徐 海 祥*1,2， 瞿 洋2， 余 文 曌1,2

( 1.武汉理工大学 高性能船舶技术教育部重点实验室, 湖北 武汉 430063；2.武汉理工大学 交通学院, 湖北 武汉 430063 )

针对动力定位船舶定点定位过程中的高低频运动特性，设计了一种基于无源滤波的反步逆最优控制器．首先建立船舶的非线性方程，再利用线性化方程对应的Riccati方程对船舶非线性方程进行反步变换，最后基于Lyapunov函数设计了未建模扰动环境力自适应律和渐进稳定的控制律，同时满足了局部性能指标和全局性能指标．该方法从一个新的角度解决定点定位过程中船舶非线性系统最优控制的问题，避免了传统H∞鲁棒控制需要求解Hamilton-Jacobi-Isaacs(HJI)方程的问题，保证了整个滤波和控制系统的稳定性．同时还研究了误差和控制权矩阵Q和R对系统性能的影响，确保了船舶低速定位过程中的能耗最优．动力定位船舶定点定位的仿真结果验证了该方法的有效性．

动力定位；无源滤波；反步变换；最优控制

0 引 言

动力定位技术已广泛用于深水钻井、海底管线的检测和调查、水下机器人作业、水下工程施工、油井增产措施和维修、平台供应、穿梭油船、浮式采油(有或无储油设备)等作业中．对于海上长时间定位的船舶，船舶的滤波和最优控制问题对于节省燃料和减少污染具有重要意义．

传统动力定位(DP)系统通常假定运动方程在36个艏向角每隔10°可线性化，并利用线性Kalman滤波滤除船舶的高频运动．对于每10°的线性化运动方程，最优的Kalman滤波器相关参数和反馈控制器增益都需要随着线性化过程不断调整[1]，并且相应的噪声协方差矩阵需要在线自适应估计[2]．相较于Kalman滤波，无源滤波参数易整定，并且实船试验也验证了其有效性[1]．此后，Fossen论述了在低速和恒定速度时，船舶系统具有良好的无源性，克服了无源理论在船舶控制系统中应用的局限性[3]．在无源理论的基础上，卜德华等结合PID控制器验证了无源滤波器对滤除船舶位置和艏摇角高频信息的有效性[4]．针对船舶定点状态环境最优问题，Fossen等提出了环境最优艏向控制，使船舶能根据外部缓变环境力自动调节艏向，从而达到减小能耗的目的[5]．对于固定艏向定位作业，最优控制问题通过设计H∞鲁棒控制器来解决，但此方法需要求解复杂的Hamilton-Jacobi-Isaacs(HJI)方程[6-7]．为了克服环境荷载对船舶系统的影响，Ngongi等利用H∞鲁棒控制来抵抗外荷载，并用TS模糊模型来逼近DP系统，最后通过求解LMI方程来保证该TS模糊控制器的稳定性[8]．相较于H∞鲁棒控制，反步积分控制设计过程简单，被广泛应用于船舶动力定位系统的设计当中[9-10]．为了满足执行机构动态特性的要求，Morishita等以及徐海祥等将执行机构的动态特性考虑到反步积分控制器的设计过程中，使控制输出更加平滑，减小了执行机构的磨损[11-12]．由于反步积分控制器的设计基于船舶数学模型，模型的准确性对控制效果有一定的影响．为了避免求解HJI方程，Ezal等针对单输入单输出系统，首先提出了一种反步逆最优控制器，将H∞最优控制理论和反步积分控制理论相结合，同时满足了局部最优和全局最优的性能指标[13]．在Ezal等的基础上，Strand等将单输入单输出的反步逆最优控制理论推广到多输入多输出的锚泊辅助动力定位中[14]．随后，Strand等又将反步逆最优控制器和无源滤波相结合，进一步推广了反步逆最优理论并保证了整个系统输入状态的稳定(input-to-state stable)[15]．由于多输入多输出的锚泊辅助动力定位系统不具有一般性，Kim等在Ezal和Strand等的基础上，推导了多输入多输出系统的一般理论形式[16]．谢文博等在Strand等的基础上，根据船舶动力定位循迹控制中时变期望位置的特点，推广设计了时变反步逆最优控制[17]．

以上文献大都侧重于滤波器或者控制器的设计稳定，而较少考虑到滤波和控制器之间的相互影响，有时无法保证整个滤波和控制系统的稳定性．在Strand等的研究基础之上，本文结合动力定位定点控制的具体要求，进一步完善反步逆最优控制理论在船舶动力定位系统中的应用，研究误差和控制权矩阵Q和R对系统性能的影响，设计一种自适应反步逆最优控制器，以保证整个滤波和控制系统的稳定性，降低船舶低速定位过程中的能耗．

1 数学模型及其变换

1.1 船舶动力定位数学模型

建立如图1所示的3个坐标系．在大地坐标系XEYEZE下，船舶当前低频运动位置和船舶期望位置分别为η=(xyψ)T和ηd=(xdydψd)T．在船舶运动坐标系XYZ下，船舶当前低频运动速度和期望速度分别为v=(uυr)T和vd=(udυdrd)T，其坐标系原点位于船中纵剖面与重心G相距xg处．船舶固定坐标系XDYDZD原点OD位于(xd,yd)，相对于北东坐标系旋转了ψd．船舶固定坐标系实际是为控制器的设计而引入的，可以认为是一个“控制坐标系”，其避免了船舶期望位置ηd对控制器的影响，使得船舶在期望位置ηd附近拥有良好的控制效果[14]．

大地坐标系和船舶运动坐标系下，船舶动力定位数学模型为[18]

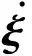
(1)

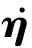
(2)

(3)

(4)

y=η+Cωξ

(5)

式中：Aω为包含波浪主频率ω0和相对阻尼ζ的定常矩阵；ωω和Eω分别为高斯白噪声及其幅值矩阵；J(η)为坐标系转换矩阵；b∈R3×1，是作用于船体上的环境扰动力，包括二阶波浪慢漂力、风和流的作用力；T为大时间常数矩阵；ωb为均值为零的高斯白噪声矩阵；Eb为高斯白噪声的幅值矩阵；M∈R3×3，为船舶惯性矩阵；D∈R3×3，为线性阻尼矩阵；τ∈R3×1，为作用于船体上的推力；y为船舶测量位置；Cωξ为船舶高频运动位置，Cω=(0I)．模型中相关矩阵的具体形式为

M=m-Xu．000m-Yυ．mxg-Yr．0mxg-Nυ．Iz-Nr．æèçççöø÷÷÷，

当船舶前进速度不为零时，矩阵D一般是非线性的；但对于零速或者恒定速度，矩阵D可以假定为线性的[1]．

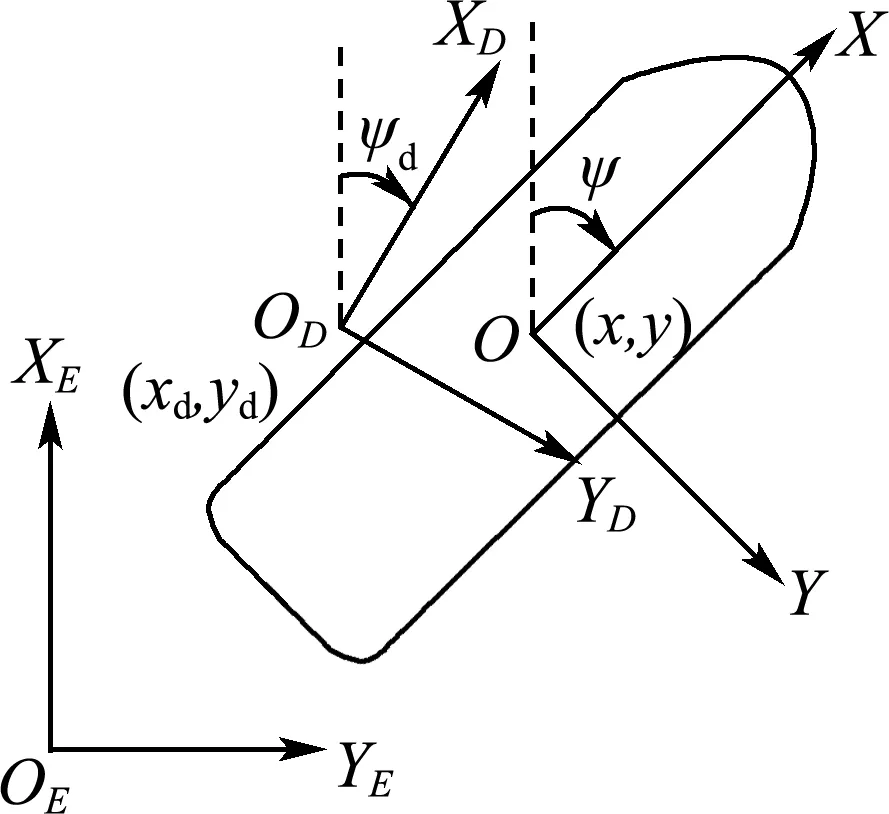
图1 大地、船舶运动和船舶固定坐标系

1.2 基于数学模型的无源滤波器设计

20世纪90年代，机器人等领域的无源控制已得到了较大的发展[19]，而船舶无源控制直到90年代后期才得到应用，限制无源理论在船舶中应用的原因是船舶的附黏水质量和阻尼项会随着船舶在海浪中的遭遇频率以及船速的变化而变化[3]．在利用无源理论设计船舶的滤波器时，需要考虑船舶是否具有无源性．Fossen已论证了当船速较低时船舶具有良好的无源性[3]．在一般工况下，环境扰动力矩对船艏的扰动角度在1°以内，而极限海况的扰动角度在5°以内，因此可以做出如下的合理假设：

J(η)≈J(y)

(6)

根据文献[1]和[18]，利用式(6)并结合船舶动力定位数学模型可设计如下船舶无源滤波器：

ξ＾．=Aωξ＾+K1y

(7)

η＾．=J(y)v＾+K2y

(8)

b＾．=-T-1b＾+K3y

(9)

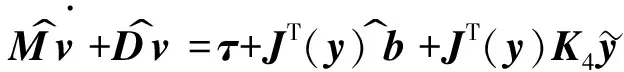
Mv＾．+Dv＾=τ+JT(y)b＾+JT(y)K4y

(10)

(11)

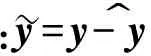
：y =y-y＾

式中；K1∈R6×3，K2，K3，K4∈R3×3，为滤波器增益矩阵．为使滤波器稳定，结合Kalman-Yakubovich-Popov引理并利用频域理论可以确定滤波器的相关增益矩阵[1]．

1.3 低频运动数学模型的变换

在大地坐标系XEYEZE和船舶运动坐标系XYZ下，无源滤波器设计用到的是低频运动数学模型(8)和(10)．为了避免船舶期望位置ηd对控制器设计的影响，控制器设计所用到的低频运动模型为船舶固定坐标系XDYDZD和船舶运动坐标系XYZ下的变换模型．在XDYDZD下，偏差向量可以表示为[14]

e=JT(ηd)(ηd-η)

(12)

记Jd=J(ηd)，Je=JT(ηd)J(η)，并考虑如下关系：

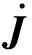
(13)

(14)

对式(12)求导有

(15)

在定点定位和状态保持控制中，期望位置偏差ed=(exdeydeψd)T和定位点处期望速度vd均为0，且滤波器的输出是控制器的输入．因此，式(15)可以简化为

e＾．=-Jev＾-JTdK2y

(16)

同时，式(10)可以写为

v＾．=-M-1Dv＾+M-1u+JTeJTdK4y

(17)

式中

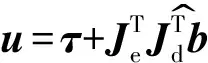
u=τ+JTeJTdb＾

(18)

x．=f(x)+Bu+Hy

(19)

式中

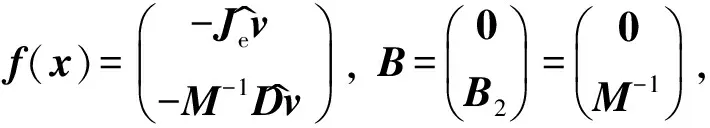
f(x)=-Jev＾-M-1Dv＾æèççöø÷÷，B=0B2æèçöø÷=0M-1æèçöø÷，

x．=Ax+Bu+H0y

(20)

式中

式(19)和(20)为船舶低频运动方程(8)和(10)的变换形式，两式均计及了船舶的期望位置ηd，避免了ηd对控制器设计的影响．

2 控制器设计

2.1 控制目标

(1)局部最优目标

系统在所设定的期望位置xd=0附近时，要实现的控制目标是对于式(20)的线性系统，设计一个稳定的控制律，以满足如下的性能指标：

(21)

式中：误差权矩阵Q和控制权矩阵R均为对称正定矩阵．对于最优的衰减系数γ*，衰减系数γ应满足γ>γ*．

(2)全局最优目标

系统最终要实现的控制目标是对于式(19)的非线性系统，设计一个全局渐进稳定的控制律，以满足如下的性能指标：

(22)

式中：q(x)和R*(x)为非线性系统中待确定的正定部分，其在反步逆最优设计过程中满足以下局部约束条件[15]：

R*(0)=R

(23)

(24)

因此，当船舶靠近设定点xd=0时，全局渐进稳定的控制律将退化为线性H∞(LQ)控制律，此时局部最优目标得到满足．

2.2 线性反步变换

局部最优性能指标Jl所对应的广义Riccati代数方程为

(25)

正定矩阵P可以分解为

P=LTΔL

(26)

式中：L为下三角矩阵，Δ为正定分块对角矩阵，

利用式(26)，可将式(25)转化为

(27)

式中

设定新的变量z，通过反步变换，满足全局目标的非线性系统式(19)有如下映射关系[20]：

(28)

z．=Az+B0ul+H0y

(29)

考虑如下Lyapunov函数：

V=zTΔz

(30)

对式(30)求导并结合式(29)的线性系统，局部最优目标所对应的线性H∞控制律为

(31)

此时，Lyapunov导函数满足

V．≤-zTQz-uTRu+γ2y Ty

(32)

在后文的控制器设计中，将会用到非线性反步逆最优设计方法来构建与式(29)相类似的非线性变换方程．在非线性反步逆最优构造过程中，都会确定每一步的虚拟控制量αi，最终存在全局最优目标所对应的控制律：

(33)

满足

V．≤-q(z)-uT∗R∗(z)u∗+γ2y Ty

(34)

其中q(z)和R*(z)的正定过程将会在后文中给出．

2.3 非线性反步变换

反步逆最优控制器的设计首先通过构建与式(29)相类似的非线性变换方程，再利用Lyapunov函数(30)推导反步逆最优控制律．非线性变换方程的推导过程总共可分两步进行．

步骤1 定义第一个偏差向量为

(35)

对式(35)求导得

z．1=α1+(-Jev＾-α1)+H1y

(36)

αh=-Π(z1)z1

Ω(z1)=diag{3ρ1z1,3ρ2z2,3ρ3z3}

式中：z1=(z1z2z3)T，ρ1、ρ2、ρ3为正常数．

定义第2个偏差向量为

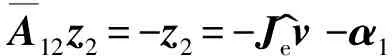
A12z2=-z2=-Jev＾-α1

(37)

因此

z．1=α1-z2+H1y

(38)

步骤2 对式(37)求导得

(39)

式中

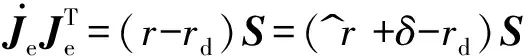
J．eJTe=(r-rd)S=(r＾+δ-rd)S

(40)

(41)

(42)

式中

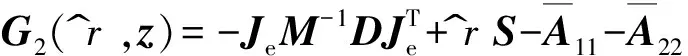
G2(r＾，z)=-JeM-1DJTe+r＾S-A11-A22

综合式(38)和(42)可得与式(29)相类似的非线性变换方程：

z．=Az+Bu+Gz+Hy +Σ

(43)

式中

2.4 反步逆最优控制器设计

若用无源滤波器中的式(9)作为未建模环境力的估计，则可选取和式(30)相同的Lyapunov函数．虽然式(9)能够实现对未建模环境力的跟踪，但是为了获得较好的滤波效果，式(9)中的增益矩阵会受到限制，使得未建模环境力的跟踪效率并不高．为了提高环境力的跟踪效率，这里采用另外一种积分操作，可以取如下Lyapunov函数：

(44)

(45)

B2u+H2y +Σ2)+2zT1Δ1H1y -2b TΓ-1b＾．

(46)

将式(27)代入上式，则

(47)

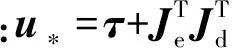
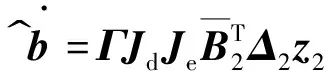
b＾．=ΓJdJeBT2Δ2z2

(48)

(49)

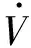
(50)

式中

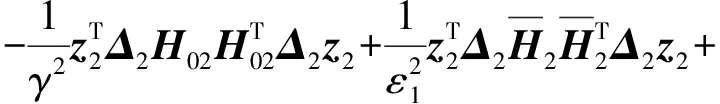
反步逆最优控制律可以取为

(51)

若令

(52)

则有

(53)

式中：q(z)应该满足正定条件，在假设船舶速度v和高频运动艏向角速度δ有界的情况下，存在有界正实数β1和β2使得Υ满足[15]

(54)

为了使整个系统稳定，q(z)需满足

(55)

结合式(54)和(55)，存在0<θ<1，使式(53)满足

V．≤-(1-θ)q(z)-uT∗R∗u∗+γ2y Ty

(56)

若q(z)满足正定条件，则

(57)

方式一

(58)

方式二

(59)

式中χ为正定矩阵，可取为

(60)

方式三

R-T∗=u1(r＾，z)I+u2(r＾，z)R-1

(61)

(62)

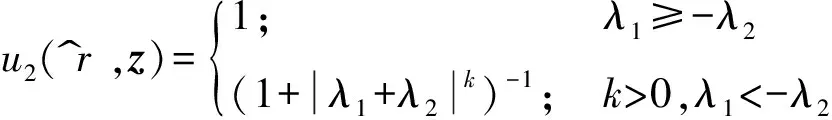
u2(r＾，z)=1；λ1≥-λ2(1+λ1+λ2k)-1；k>0，λ1<-λ2{

(63)

(64)

(65)

式中：λmax(*)表示求取*的最大特征值．为了操作的简便，这里选用第3种选取方式．

3 仿真结果与分析

下面将通过计算机仿真来验证无源滤波和反步逆最优算法的有效性．如图2所示，本文仿真模型为缩尺比为1∶20的平台供应船模，船舶的惯性矩阵和阻尼矩阵通过CFD理论计算得到，船舶模型相关参数、环境力参数以及控制器等相关参数如表1所示，环境荷载的加载方式详见文献[18]．

为检验未建模环境力自适应律效果，使船舶状态保持控制，初始时刻船舶位置为η0，期望位置也为η0，初始时刻船舶3个方向未建模环境力和力矩均设置为零．船舶在时刻t=200 s时受到表1中的环境力作用，在t=1 800 s环境力消失．船舶在东向、北向和艏向的位置如图3所示．固定坐标系下3个方向的自适应未建模环境力如图4所示．相应的权矩阵选取为

图2 平台供应船模

表1 相关参数设定值

为检验权矩阵Q和R对DP系统的能耗影响，使船舶作中近距离定点定位控制，初始时刻船舶位置为η0，期望位置为ηd=(5 m 5 m π/4)T，无环境力干扰．选取4组权矩阵．

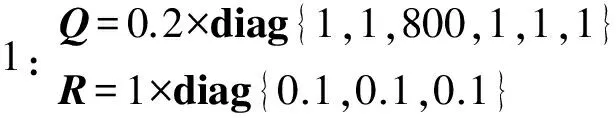
为了比较权矩阵对船舶能耗的影响，取如下总推力性能指标：

(b) 船舶状态保持北向位置

(c) 船舶状态保持艏向位置

图4 船舶状态保持自适应未建模环境力

权矩阵为参数1、2、3和4时，总推力性能指标如图5所示，船舶低频东向位置、低频北向位置和低频艏向位置如图6所示．

针对本文中所涉及的无源滤波器，状态保持仿真实验展示了相应的滤波效果和未建模环境力

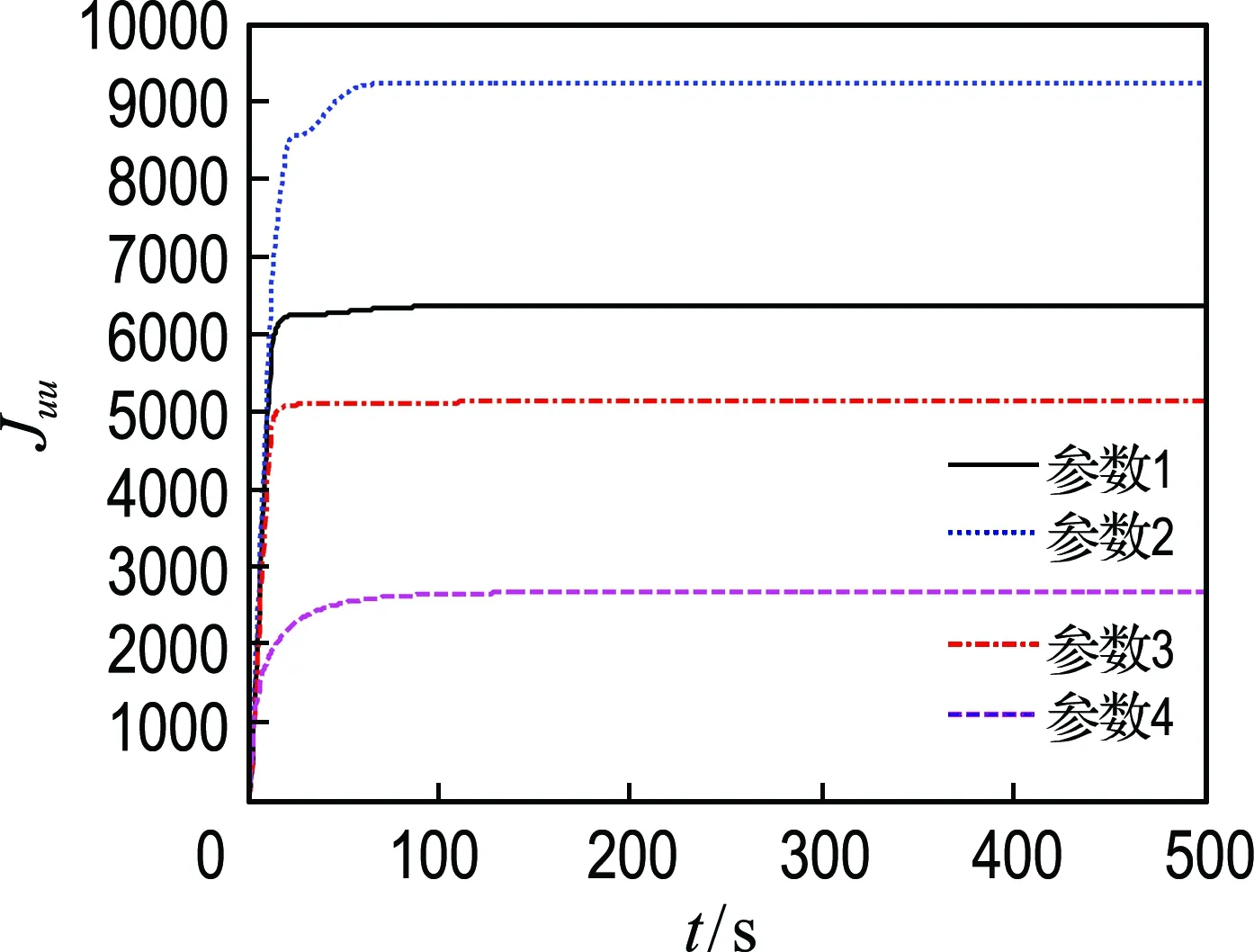
图5 总推力性能指标

(a) 船舶低频东向位置

(b) 船舶低频北向位置

(c) 船舶低频艏向位置

图6 不同权矩阵下的控制效果

Fig.6 The control results of different positive cost matrices

自适应律的效果．在突变未建模环境力的作用下，图4展示了环境力自适应律良好的跟踪效果．图3展示了在自适应未建模环境力和实际环境力相近时，船舶的位置和艏向滤波效果良好，在很大程度上滤除了高频运动．在t=200 s至t=1 800 s，自适应未建模环境力和实际环境力存在较大偏差，导致船舶位置估计尤其是艏向角估计和实际低频位置存在一定的偏差．造成未建模环境力和实际环境力有偏差的原因往往是突风、大浪或者激流等．由于控制是响应缓变环境力，变化较大且频繁的外部环境力对船舶控制将会是一个巨大的挑战．

图5展示了不同权矩阵所对应的总推力性能指标，船舶的低速运动意味着船舶较长的响应时间，与此同时相应的能耗也较小．图6给出了不同权矩阵对定位效果的影响．根据权矩阵的定义可知，参数Q的前3个元素对应船舶的位置权重，而后3个元素对应船舶的速度权重；参数R对应控制器的输出推力权重．参数2相较于参数1增大了位置权重，船舶的速度有所增大，相应的超调量和响应时间等系统响应特性都得到了改善．参数3相较于参数1增大了推力权重，船舶位置的响应时间变长和超调量有所增加，这是由于增大推力权重会在一定程度上限制控制器的推力输出．参数4相较于参数1增大了船舶速度权重，船舶位置的响应时间明显变长，且基本无超调，这是因为增大速度权重限制了船舶速度．值得注意的是，过大的船舶速度会破坏船舶系统的无源性，即船舶的附加质量和阻尼明显的非线性，将会对船舶系统的稳定性有着明显的影响．因此，为了使整个动力定位控制系统稳定，控制船舶的速度不宜过高是十分必要的．

4 结 语

本文针对动力定位船舶定点定位问题设计了一种基于无源滤波的自适应反步逆最优控制器，避免了H∞鲁棒控制器设计过程中需要求解HJI方程的问题，满足了局部最优和全局最优的性能指标，对外界缓变未建模环境力进行补偿的同时，也保证了无源滤波和控制整个系统的稳定性．不同权矩阵Q和R对动力定位控制系统的响应时间、超调量等动态特性和控制推力有着直接的影响，在满足系统稳定性的条件下，可通过优化性能权函数Q和R以达到提高控制精度与降低能耗的目的．

[1] FOSSEN T I, STRAND J P. Passive nonlinear observer design for ships using Lyapunov methods:full-scale experiments with a supply vessel [J]. Automatica, 1999, 35(1):3-16.

[2] FOSSEN T I, PEREZ T. Kalman filtering for positioning and heading control of ships and offshore rigs [J]. IEEE Control Systems, 2010, CST-29(6):32-46.

[3] FOSSEN T I. Nonlinear passive control and observer design for ships [J]. Modeling, Identification and Control, 2000, 21(3):129-184.

[4] 卜德华,徐海祥,李文娟,等. 基于非线性无源滤波器的船舶动力定位仿真[J]. 武汉理工大学学报, 2013, 35(10):69-73.

BU Dehua, XU Haixiang, LI Wenjuan,etal. Simulation of ship dynamic positioning based on nonlinear passive filter [J]. Journal of Wuhan University of Technology, 2013, 35(10):69-73. (in Chinese)

[5] FOSSEN T I, STRAND J P. Nonlinear passive weather optimal positioning control (WOPC) system for ships and rigs:experimental results [J]. Automatica, 2001, 37(5):701-715.

[6] WU Huaining, LUO Biao. Neural network based online simultaneous policy update algorithm for solving the HJI equation in nonlinear control [J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(12):1884-1895.

[7] CHEN W, ANDERSON B D O. On the convergence rate of the Leake-Liu algorithm for solving Hamilton-Jacobi-Bellman equation [J]. IFAC Proceedings Volumes, 2011, 44(1):8064-8069.

[8] NGONGI W E, DU J, WANG R. Robust fuzzy controller design for dynamic positioning system of ships [J]. International Journal of Control Automation & Systems, 2015, 13(5):1294-1305.

[9] Jr. ZAKARTCHOUK A, MORISHITA H M. A backstepping controller for dynamic positioning of ships:numerical and experimental results for a shuttle tanker model [J]. IFAC Proceedings Volumes, 2009, 42(18):394-399.

[10] WITKOWSKA A. Control system design for dynamic positioning using vectorial backstepping [J]. Scientific Journals of the Maritime University of Szczecin, 2013, 108(36):182-187.

[11] MORISHITA H M, SOUZA C E S. Modified observer backstepping controller for a dynamic positioning system [J]. Control Engineering Practice, 2014, 33:105-114.

[12] 徐海祥,瞿 洋,余文曌,等. 基于动态执行机构的欠驱船舶循迹控制[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(1):6-10.

XU Haixiang, QU Yang, YU Wenzhao,etal. Path following for underactuated marine craft with actuator dynamics [J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2016, 40(1):6-10. (in Chinese)

[14] STRAND J P, EZAL K, FOSSEN T I,etal. Nonlinear control of ships:a locally optimal design [M] // Preprints of the IFAC NOLCOS 1998. Enschede:The Netherlands, 1998:732-738.

[15] STRAND J P, FOSSEN T I. Nonlinear output feedback and locally optimal control of dynamically positioned ships:Experimental results [C] // Proceedings of IFAC Conference on Control Application in Marine Systems. Fukuoka:IFAC, 1998:89-95.

[16] KIM H, BACK J, SHIM H,etal. Locally optimal and globally inverse optimal controller for multi-input nonlinear systems [C] // Proceedings of 2008 American Control Conference. Seattle: AACC, 2008:4486-4491.

[17] 谢文博,付明玉,张 健,等. 动力定位船舶自适应反步逆最优循迹控制[J]. 中国造船, 2013, 54(3):58-69.

XIE Wenbo, FU Mingyu, ZHANG Jian,etal. Adaptive backstepping inverse optimal tracking control of dynamic positioning vessel [J]. Shipbuilding of China, 2013, 54(3):58-69. (in Chinese)

[18] FOSSEN T I. Handbook of Marine Craft Hydrodynamics and Motion Control [M]. New York:John Wiley & Sons, 2011.

[19] BERGHUIS H, NIJMEIJER H. Passivity approach to controller-observer design for robots [J]. IEEE Transactions on Robotics & Automation, 1993, 9(6):740-754.

[20] FOSSEN T I, STRAND J P. Tutorial on nonlinear backstepping:Applications to ship control [J]. Modeling, Identification and Control, 1999, 20(2):83-135.

Inverse optimal backstepping control of dynamic positioning ships

XU Haixiang*1,2, QU Yang2, YU Wenzhao1,2

( 1.Key Laboratory of High Performance Ship Technology of Ministry of Education, Wuhan University of Technology, Wuhan 430063, China； 2.School of Transportation, Wuhan University of Technology, Wuhan 430063, China )

In view of the characteristics of high and low frequency motion in ship dynamic locating and positioning, an inverse optimal backstepping controller is designed cascaded with a passive filter. Firstly, the nonlinear equation of the ship is established. Then, the Riccati equation corresponding to the linear equation is used to carry out the backstepping transformation of the nonlinear equation. Finally, the adaptive law and the asymptotic stable control law for disturbed environmental force without modeling are designed based on the Lyapunov function, which meets both the local cost function and global cost function. This new approach obtains a solution of the optimal control of nonlinear system in a new direction, avoids solving the Hamilton-Jacobi-Isaacs(HJI) equation in traditionalH∞controller design and simultaneously guarantees the stability of filter and controller. The influences of error and control weight matrixQandRon the system performance are discussed, and the optimal energy consumption during dynamic positioning of ship at slow speed is achieved. The simulation results of a dynamic locating and positioning ship show the effectiveness of this approach.

dynamic positioning; passive filter; backstepping transformation; optimal control

1000-8608(2017)01-0046-09

2016-01-07；

2016-09-20．

国家自然科学基金资助项目(61301279,51479158)；中央高校基本科研业务费专项资金资助项目(163102006).

徐海祥*(1975-),男,教授,博士生导师,E-mail:qukaiyang@163.com；瞿 洋(1991-),男,硕士生,E-mail:yangqu91@163.com；余文曌(1989-),男,讲师,E-mail:yuwenzhao1989@gmail.com.

U674.38

A

10.7511/dllgxb201701007