三次函数新热点 发散思维巧解题
2017-02-06宋惠英
宋惠英
(江苏省江阴高级中学 214400)
高考链接(2017·江苏)已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
(2)证明:b2>3a;
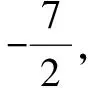
2017年江苏数学高考卷的最后一道压轴题是以三次函数为背景的,结合了函数的极值、零点的概念,考查了函数解析式与定义域、不等式的证明、导数、函数的极值最值和零点等一系列知识,可见高考数学命题正体现了以基础知识为根本,提升能力为目的的命题思路,三次函数也再次引起广大师生的关注,成为新的热点.本文以一道常见的三次函数题为例,在基本知识熟练应用的基础上发散思维,探索三次函数的解题思路和方法.
一、问题背景
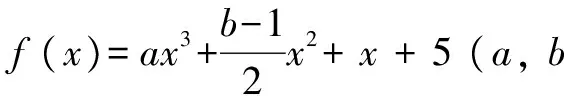
(1)求证:x1x2>0;
(2)求证:(b-1)2=16a2+4a;
(3)求实数b的取值范围.
这道题以三次函数为背景,以极大极小值为载体,综合运用导数、二次函数、不等式等数学基本知识和基本方法,是一道精心设计的函数不等式综合题,条件简洁,入手顺畅,方法多样,能有效激发学生思维,是一道值得回味的好题.
二、分析问题
根据题目的条件,学生马上就能入手,对原函数求导,可知f′(x)=ax2+(b-1)x+1(a>0),那么x1、x2就是f′(x)=0的两根,x1x2的符号可以由韦达定理来判断.第二小题也不难,抓住|x1-x2|=4的条件,代入韦达定理,也很快可以解决.
但是第三问求实数b的取值范围就不容易解决了,虽然第二问有a,b的关系,但是这是个二次式,同时,条件中的|x1|<2,且|x1-x2|=4的使用也情况复杂.可以先确立根的范围,从二次方程根的分布入手,也可以试试不等式的性质来处理.
三、解决问题
解(1)f′(x)=ax2+(b-1)x+1(a>0).
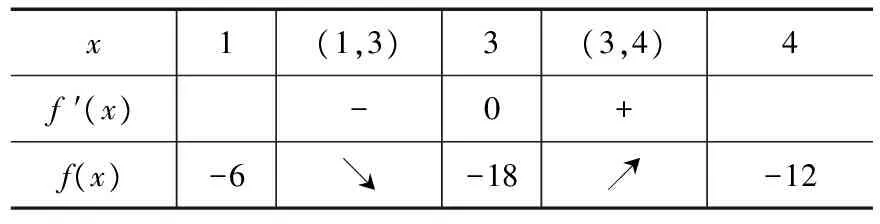
由题知f′(x)=0的两根为x1,x2且x1 ∴(b-1)2=16a2+4a. (3)[法一]:确立根的范围,挖掘隐含条件. ∵|x1|<2,x1 ∴x1>0即0 从而(4a+1)2<2(1-b)2=4(16a2+4a), ∵|x1|<2,x2=x1+4, ∴2 把x1、x2用a,b表示,完美处理条件|x1|<2,且|x1-x2|=4 [法三]:同上得f′(2)=4a+2b-1<0且1-b>0, ∴4a+1<2(1-b). 转化为关于b的不等式,再求解, [法四]:分析可得0 ∴2 结合二次函数图象, (1)×9-(2)得:12(b-1)+8<0,转化为二次方程根的分布问题, [法五]:由题知f′(x)=0的两根为x1,x2且x1 令t=x1+2(2,4), 已知函数f(x)=x3-ax2-3x. 1.若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围; 3.在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点?若存在,请求出实数b的取值范围;若不存在,请说明理由. 解(1)f′(x)=3x2-2ax-3. ∵f(x)在[1,+∞)是增函数, ∴f′(x)在[1,+∞)上恒有f′(x)≥0,即3x2-2ax-3≥0在[1,+∞)上恒成立, ∴a=4,∴f(x)=x3-4x2-3x. 则当x变化时,f′(x)与f(x)的变化情况如下表: x1(1,3)3(3,4)4f′(x)-0+f(x)-6↘-18↗-12 ∴f(x)在[1,4]上的最大值是f(1)=-6. (3)假设存在实数b使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程x3-4x2-3x=bx恰有3个不等实根. ∴x3-4x2-3x-bx=0,∴x=0是其中一个根,∴方程x2-4x-3-b=0有两个非零不等实根. ∴存在满足条件的b值,b的取值范围是b>-7且b≠-3. 变量、字母较多的问题是高中数学中常考的问题,三次函数又是高考中的热点问题,但是三次函数往往能通过求导转化为我们熟悉的二次函数,从而和二次方程,不等式联系起来.所以要提高数学的解题能力,第一要有扎实的基础,熟练掌握利用导数求函数的极值或最值的方法,解题的关键是首先要正确求导,准确记忆常用函数的求导公式及求导法则,其次令导函数等于零,列表,根据表格确定极值,进而确定最值,注意不能忽视边界.第二要多研究问题,抽丝剥茧,转化联想,恒等变形,消元化一,结合图象,一题多解,必能在解题能力上上一个台阶. [1]蔡广军.发散思维 有的放矢——从一道模拟题浅谈最值问题转化角度[J]. 福建中学数学,2014(Z1). [2]李静.例说高中数学最值问题[J].数理化解题研究(高中版),2013(04).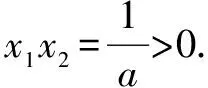
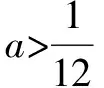
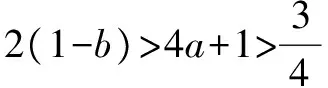
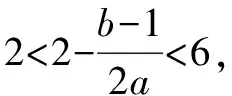
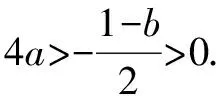
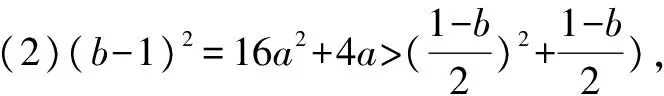
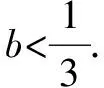
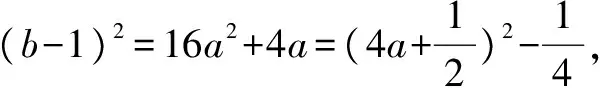
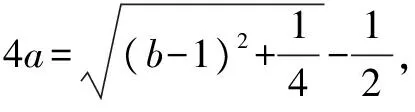
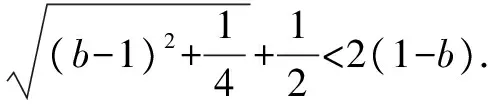
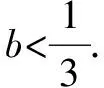
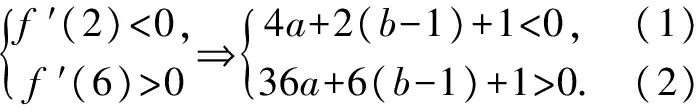
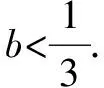
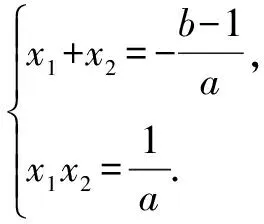
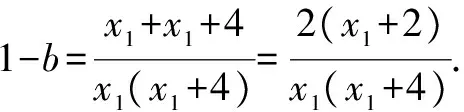
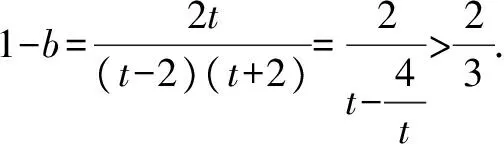
四、联想比较
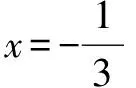
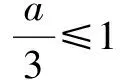
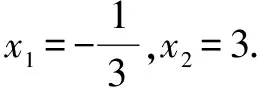
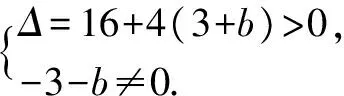
五、回顾反思
