神奇的杨辉三角

刘彦永

(东北师大附中 130021)

南宋的杨辉在他1261年所著的《详解九章算法》一书中记录了图1所示的三角形数表，称之为“开方作法本源”图，即现在的杨辉三角，其本质是二项式系数在三角形中的一种几何排列(如图2).杨辉三角中蕴含着许多奇妙的性质，也与许多数学问题有着密切的联系.古今中外，有许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都层深入研究过杨辉三角，下面我们一起走近杨辉三角吧.

一、杨辉三角与组合数

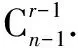
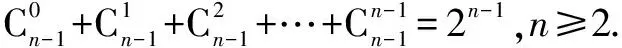
(5)每一行奇数位上的数的和与偶数位上的数的和相等，即

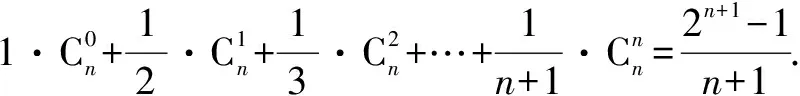
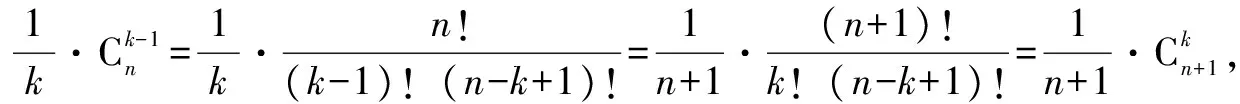
二、杨辉三角与概率问题

如图3的高尔顿板，若小球碰到阻挡物后等可能地向两侧跌落，再次遇到障碍物后继续等可能的向两侧跌落，以此类推，一直下跌，直到最终落入底层.

1.在图3的高尔顿板中，求：

(1)小球落入第4层第3个通道的概率P(4,3)；

(2)小球落入第n+1层第k(k≤n)个通道和第n+1层第k+1个通道的概率之和.

分析高尔顿板的原型为杨辉三角，利用杨辉三角的基本性质和数量关系即可解决问题.

(2)根据杨辉三角的特点有

事实上，我们可以用数学归纳法证明如下定理：

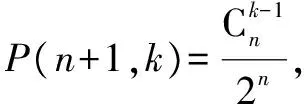
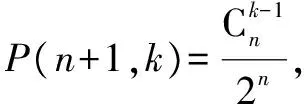
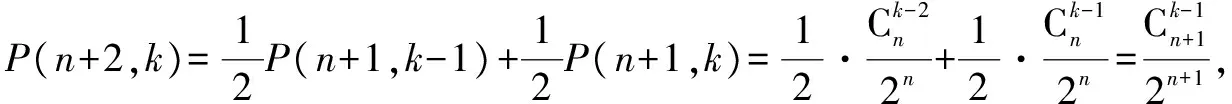
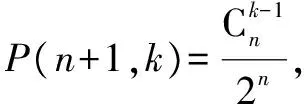
三、杨辉三角与纵横路线图

例4 纵横路线图是一类有趣的数学问题.图4是某城市的部分街道图，纵横各有5条路，从A处走到B处且路径最短，共有多少种不同的走法？

解我们把图5顺时针旋转45度，然后在交叉点标上杨辉三角对应的数，如图6.一般地，每个交点上的数就是从A处到达该点的方法数，故答案是70.

四、杨辉三角与莱布尼茨三角形

西方著名的莱布尼茨三角形要比中国的杨辉三角晚400多年.莱布尼茨三角形(如图6)和杨辉三角也有着极其密切的联系，下面通过两个试题说明.

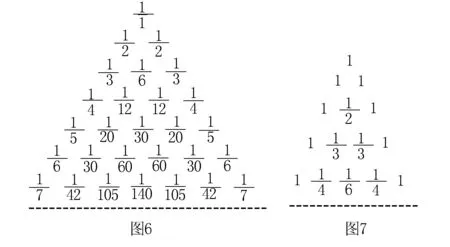
例5 如图7所示的莱布尼茨三角形中，第n+1行第k列的数为 .

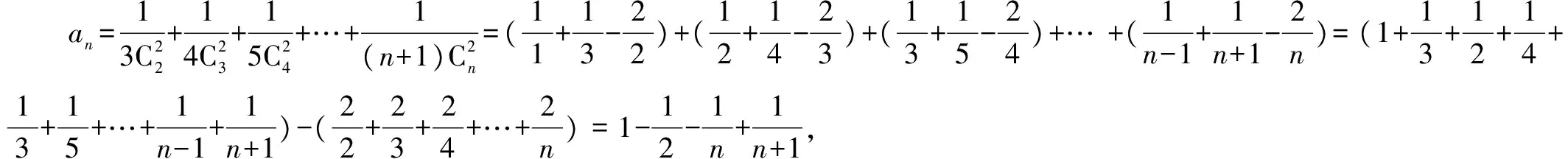
事实上，第二问的本质是求莱布尼茨三角形中从第3行第3列到第n+1行的第3列的所有数之和，结合第一问知每个数都等于其脚下两数的和，添减项就有

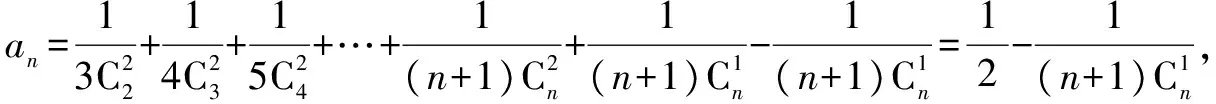
五、杨辉三角与变异的杨辉三角

例7 (2007年湖南理科)将杨辉三角中的奇数换成1，偶数换成0，得到如图8所示的0-1三角数表．从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第_____行；第61行中1的个数是_____．

第1行 1 1

第2行 1 0 1

第3行 1 1 1 1

第4行 1 0 0 0 1

第5行 1 1 0 0 1 1

…… ………………………………………

图8

解我们称以上三角数表为变异的杨辉三角，续写上表有

第6行 1 0 1 0 1 0 1

第7行 1 1 1 1 1 1 1 1

可见，第1,3,7行的数都是1，即第21-1，22-1，23-1行的数都是1.猜想第2n-1行的数都是1(可以用数学归纳法证明).因此，第26-1=63行都是1，共有64个1.

写出第62-64行，逆推知第62行共有32个1，结合图中对应关系知第61行共有32个1.

例8 (2003年全国)设{an}是集合{2s+2t|0≤s

3

5 6

9 10 12

— — — —

— — — — —

图9

(Ⅰ)写出这个三角形数表的第四行、第五行各数；

(Ⅱ)求a100.

解(Ⅰ)用(s,t)表示2s+2t，记作2s+2t=(s,t).观察发现图11的规律为：

3=20+21=(0,1)；

5=20+22=(0,2)，6=21+22=(1,2)；

9=20+23=(0,3)，10=21+23=(1,3)，12=22+23=(2,3).

按照这个规律，第四行的数是17,18,20,24，第五行的数是33,34,36,40,48.

(Ⅱ)因为100=(1+2+3+…+13)+9，所以a100=(8,14)=28+214=16640.

杨辉三角不仅与上述问题有联系，而且和斐波那契数列、谢尔宾斯基三角形、堆垛术和行列式等都有着密切的关系.这些看似独立的数学概念，通过杨辉三角，竟然建立了如此美妙的数学知识网络，这真是一件震撼人心的快事.杨辉三角中究竟还蕴含着怎样优美而神奇的规律？这值得我们进一步深入的探索.

[1]人民教育出版社，课程教材研究所数学课程教材研究开发中心.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2003.

[2]张奠宙.中学教学全书数学卷[M].上海：上海教育出版社，1983.