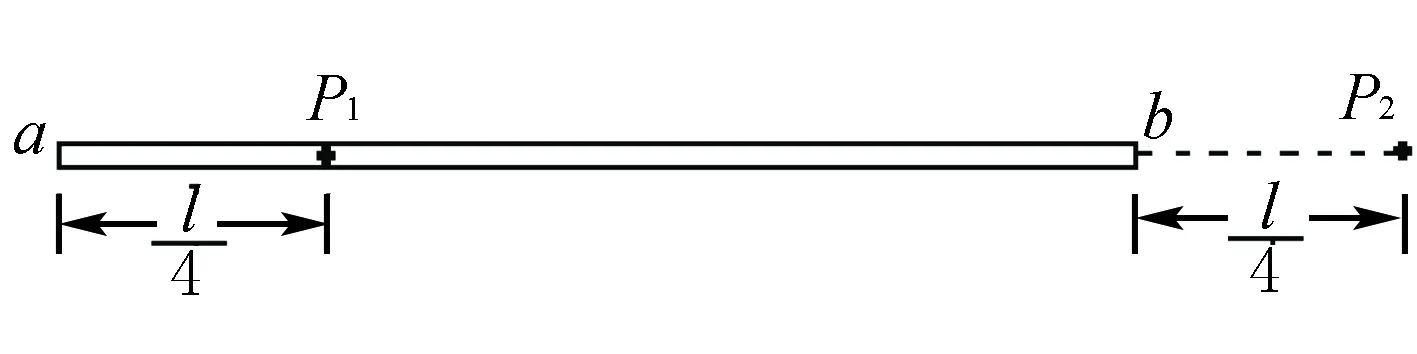高中物理解题中分割法的应用

高 超

(河北省邢台市第一中学 054300)

分割法可以将一个独立、完整的事物或过程分割成几个部分，分割的方式也是多种多样的，可以根据题型的不同，以时间进行分割，也可以是对图形、对象、位移、轨迹的分割，这样可以通过简单化的处理使不熟悉的问题变成我们熟悉的常规化问题，使问题的解题难度降低.分割法是物理解题中一种重要的思维方法.

一、分割法在重力计算中的应用

受重力作用的影响，物体在各部分重力的合力下会形成一个重力作用点——重心.求解物体重心的题型在高中物理中比较常见.

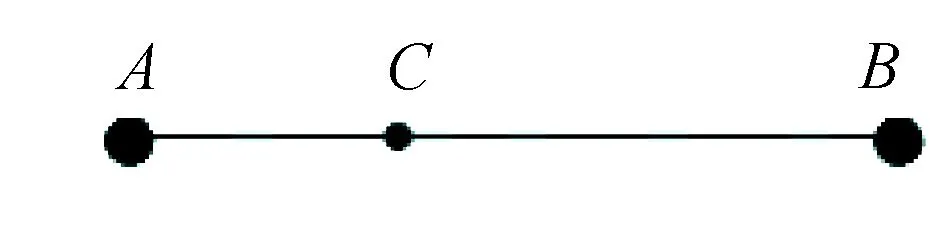
图1

A、B两个质点的质量分别为mA和mB，两个质点间以一个不计质量的轻杆连接，再以细线连接A端，可使这个结构在悬挂起来后处于平衡状态，发现杆沿竖直静止，由此可知该系统的重心处于通过杆的直线上，再将杆与杆上的C点连接，可使整个结构在悬挂时达到平衡状态，则C点就是该结构的重心.如图1所示：

GA·AC=GB·BC

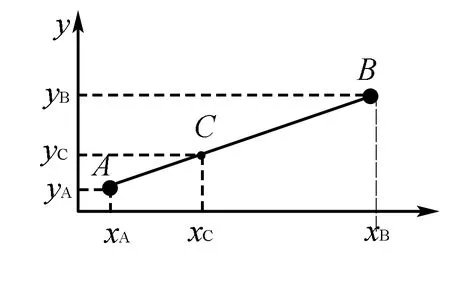
图2

这个重心问题也可放在直角坐标系中进行讨论得到答案.如图2,所采用的原理是同向平行力合成的结论或杆杠原理，可知重心C的坐标：

如果两个质点的质量相等，则两年质点联线的中点即为重心.如果两个质点的质量不同，重心自然会偏向重量更大的一边.

分析一般情况下，求重心或质心的方法有定义法、负质量法等，定义法是较常见、最基本的解法.基于直角坐标定义式，建立直角坐标，从而求得重心的位置.但是对于质量连续分布的物体，在计算时就会用到积分，这就增加了解题的难度.而负质量法本质上就是在分割法的基础上将整个结构分割成易求得质心的几个部分，从而对结构的重心进行推论，其区别晨于每个部分即可以是正质量，也可以是负质量.此时采用分割法，将整个结构分割成若干个部分，通过求分割后的各个部分的质心位置，再利用质心定义的表达式即可求得整个结构的重心位置.可以将整个结构分割成球和棒两个部分，再以同向平行力合成的方法求得重心C.如图3所示，将质点A假设为半径为R、质量为M的质球；将棒子假设为长度为l、质量为m的质棒B，分别求它们的重心.C在AB连线上，且AC·M=BC·m.如图4.

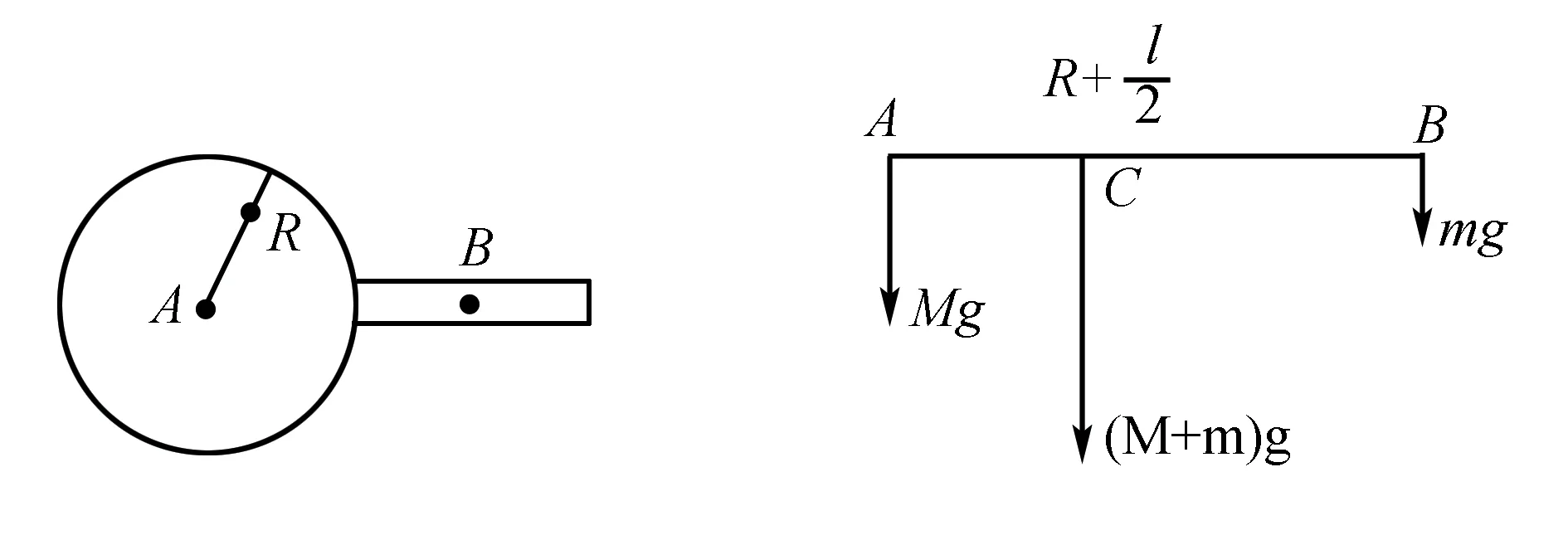
图3 图4

二、分割法在定性分析中的应用

如图5所示，以逆时针方向的电流I向原本静止的圆形线圈通电，在其直径ab上靠近b点置垂直线圈平面的固定长直导线，并通以电流I′，此时圆形线圈在磁场力的作用下会做怎样的运动？

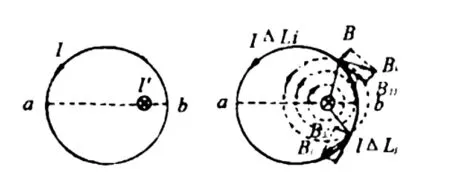
图5 图6

分析该题考查是右手螺旋定则和左手定则，一般情况下判断导体运动规律的常用方法是微元法、等效法、特殊位置法、结论法等.利用微元法，以左手定则可判断出安培力的方向.根据安培定由可知直线电流在a点上的磁场方向是竖直向上的，并平行于a点电流的方向，可知a点不受安培力的影响.针对线圈上下位置一电流元的分析可知，上边电流元的电流方向向左，而下边的电流元方向向右，电流在这个位置受磁场影响的方向是斜向上的，根据左手定则可知上边微元受到垂直于纸面向里的安培力影响，而下边的电流受垂直于纸面向外的安培力影响，使得整个线圈以直径ab为轴进行轴转动.

同样，以分割法也可得出同样的结论.我们假设将圆形圈分割后，取与直径ab对称的两个小段IΔLi和IΔL，如图6所示，将直导线产生的磁场分布画出，根据安培定则可知圆形线圈在IΔLi和IΔL两段中受安培力的影响分别产生垂直于纸面的向里、向外的力，由此得出整个线圈以直径ab为轴进行轴转动的结论.

三、分割法在定量分析中的应用

如图7所示，某力F=10 N作用于半径R=1 m的转盘的边缘上，力F的大小保持不变，但方向始终保持与作用点的切线方向一致，则转动一周这个力F做的总功是多少？

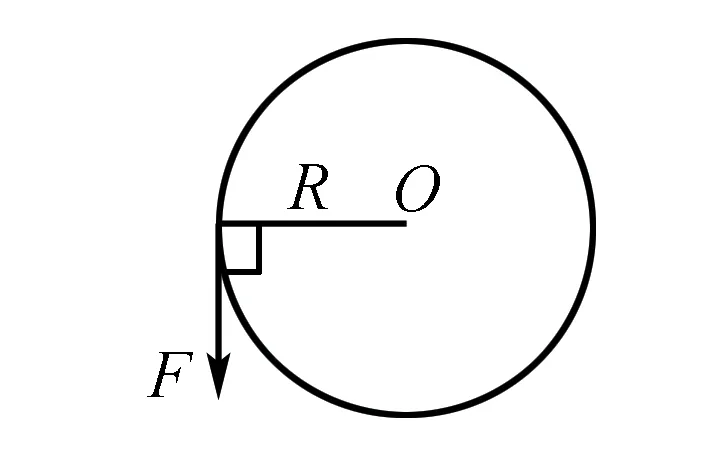
图7

分析这道题考查的是匀速圆周运动和功的计算.在恒力作用下，求力做的功为W=Fx，所以求出在力作用下通过的位移即可知道答案.然而这道题中，力F是沿着作用点的切线方向不断改变方向的，属于变力做功，因此不能直接采用以上公式进行求解.需要通过先计算力F转动一周的位移：X=2πR=2π,再计算力F通过的位移为：W=F×=10*2πR=20πJ.

采用分割法将力F的作用点轨迹分割成无限个小元段，那么在转动一周的情况下，力F的作用点位移与转动的轨迹重合，那么每一个小元段上力F所做的功为ΔW=FΔs，则转一周中各个小元段做功的代数和为这个力F做的总功，即W=F×2πR=10×2πJ=20πJ.

四、分割法在电场分析中的应用

ab是长为l的均匀带电细杆，P1、P2是位于ab所在直线上的两点，位置如图8所示．ab上电荷产生的静电场在P1处的场强大小为E1，在P2处的场强大小为E2．则以下说法正确的是( ).

A．两处的电场方向相同，E1>E2

B．两处的电场方向相反，E1>E2

C．两处的电场方向相同，E1

D．两处的电场方向相反，E1

图8

分析在只学过电荷电场或匀强电场而没有掌握杆产生电场的知识点时，以分割法将杆分成若干个点构成，再进行矢量合成，是得到答案的最佳方案.设均匀带电细杆带正电荷，对P1，均匀带电细杆左边l4和右边l4的电荷在P1点的场强叠加为零，细杆右边距P1l4到3l4处的电荷对P1点叠加后的场强为E1，方向水平向左；对P2，均匀带电细杆整个杆的电荷对P2均有场强，叠加后为E2，方向水平向右.对P1产生场强的电荷小于对P2产生场强的电荷，所以两处的场强方向相反，E1

[1]唐佳乐.高中物理学习之我见[J]. 亚太教育,2016(35).

[2]陆凤艳.论高中物理有效教学[J]. 中国校外教育,2016(11).