浅谈如何利用数形结合的方法拓展高中数学解题思路

徐 真

(山东省青岛第十五中学 266000)

一、什么是数形结合

数和形是数学学习中两个最基本的元素，是数学这一学科学习解题的基础，是攀登数学这座高山的第一阶梯.所有的数学问题都是围绕着数与形这两方面展开的.每一个几何图形都蕴含着大量的数字信息、数量关系；而数量又常常可以通过图形的方式生动形象的来表达.所以在解决数学问题过程中，常常根据数学问题里数字与答案之间某种联系，对题目进行针对性的图形分析，比如应用函数的图象来直观地说明函数的性质，这种方式统称“以形助数”；而有关于图形的问题也通常借助数字之间的关系进行思考，如应用曲线的方程来精确地阐明曲线的几何性质，统称“以数辅形”.数与形之间关系复杂相辅相成，在解析数学难题时，我们往往通过数形结合的方法把数学问题中的数量关系和空间形式相结合，通过数与形的相互解析，从而得出结论.

二、高中数学学习中存在解题思路单一的现象

数学题型千变万化，形式多样，教师在教学中不能仅仅将课本上的常规解法教授给学生，特别是当学生面对新题型，无从下手的时候，解题思路单一的问题就会暴露出来.传统的教学模式下，教师容易照本宣科，开展解题思路教学缺少学生自主参与，容易让学生坐享其成.通常学生容易将老师上课演示的解题思路变成既定程序，错误的意识到只要根据公式进行数字计算，完全不需要思考就可以将同一种类型的题目解出来.但是只要稍微将题目里的数字关系进行变化，学生便又没了解题模板，解不出题目.失去了自主参与，单一不灵活的解题思维，限定了学生解题方向.事实证明只有一种解题思路是行不通的，必须要有思维的变通性，将原有的解题模板打破，运用更灵活的解题方法，独立思考运用细致的观察力和强大的联想，对题目有一个自身的想法，才能以不变应万变，将难题迎刃而解.

三、学习方法有问题导致解题思路固定不变通

由于我国的教育模式导致的人才培养机械化，教学模式一成不变化，学生没有自主学习的意识与能力.纵观近几年的高考数学的试题，可以看出试题加强了对知识点灵活应用的考察，以及对公式巧妙转换能力的探析.这就对学生思维能力的要求加强.怎样才能提升思维能力？很多考生选择依靠题海战术，寄希望于多做题来应对变化多端的考试题，然而仅仅凭借题海战术的集中式训练，依旧难以获得适合自己的科学的思维方式，以至于收效甚微，成绩依旧没法提高.其中最主要的原因是解题思路格式化、固有化造成的，并不是学生自身“不够用功”的原因，并且就算做再多的题思维依旧被捆绑，学生很难跳出原来的思维定式.我们不要求学生掌握高深的理论，但要求学生形成一定的独特的审题思维.要学生学会如何从题目所给的条件中去寻求知识点做题，而不是利用题海战术的“知识点经验”做题，如何让学生破茧成蝶，有所改观？这里就不得不提到数形结合解题法的教学.我国著名数学家华罗庚曾说过:“数形结合百般好，隔裂分家万事休.”利用好数形结合法可以让学在重重阻碍中脱颖而出.

四、利用数形结合法解题帮助学生扩展解题思路

数形结合法在高中数学中应用广泛，与问题式教学法和逆向思维解题法一样可以帮助学生拓展解题思路，然而不同的是数形结合解题法既可以帮助学生拓展解题思路又可以解决多种数学问题，例如：集合问题，在集合运算中可以采用画数轴的方法来处理交集、并集、补集的运算，使问题简单化，解题思路明了.解决三角函数的问题，利用图象将有关三角函数的单调区间，三角函数大小值的比较等问题图象化，借助三角函数图象直观地处理问题.解决绝对值的问题，利用数轴与绝对值的性质(一点到0点的距离)得到答案，等等.下面我们来重点谈谈利用数形结合的方法来解决函数单调性的问题.

利用数形结合解决函数单调性问题.函数单调性是函数的一个重要的性质，是高考的热点考点之一，在解决相关问题时我们要先确定函数单调性和函数的单调区间，数形结合是确定函数单调性的最佳方法，函数的单调区间形象直观地反映在图象上.

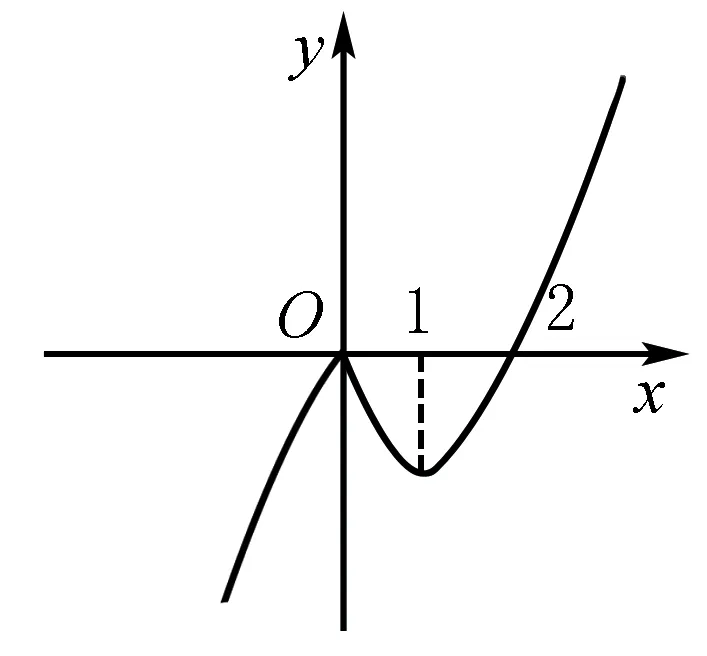
例确定函数y=x|x|-2|x|的单调区间

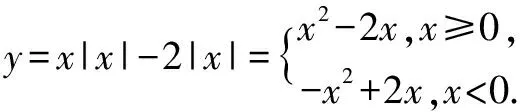
画出草图由函数图象得知函数的单调区间为：

增区间(-∞,0],[1,+ ∞);减区间为[0,1].

通过数形结合的方法解决类似题目，学生不仅可以通过计算得到答案，还能够在图形上直观地看到答案，加以验证检查.放弃原有的仅仅利用数字间的关系解题，打破思维的界限以及固有的传统的解题思路，真正做到了利用多种角度看问题，采用图形图象的方式解题.

在新课改下，如何有效地提高学生的主体意识是教育工作者最重视的话题，当学校真正落实学生主体地位，感到自己是数学课堂的主人，才能达到促进学生自主发展的目的，同时这也是素质教育的核心思想.让学生在课堂学习中有着明确的主体意识，通过多角度思考问题，运用多种解题思路分析问题.强烈的主体意识能激发学生的学习兴趣，独立思考探索新知，学会举一反三，在老师教学的基础上能用到多种解题方法和思路.

综上所述，利用数形结合的方法解析高中数学例题，能有效地拓展学生的解题思路，还能激发学生学习的积极性以及主动性，培养学生的发散思维.所以，高中数学教学中，教师有必要帮助学生利用好数形结合法的解题优势，帮助学生通过变换性思维去解决实际问题.

[1]李启龙.第三篇:数形结合思想在函数问题中的应用[J].广东教育(高中版),2015(2).

[2]梁军虎.例析数形结合在高考函数中的应用[J].现代教学研究,2012(2).