二项展开式中指定项系数求法“全扫描”

蒋 敏

(四川省南充龙门中学 637130)

一、通项分析法，开门见山，直捣黄龙

1.求第m项：此时k+1=m，直接代入通项；

2.求常数项：即这项中不含“变元”，令通项中“变元”的幂指数为0建立方程；

3.求有理项：令通项中“变元”的幂指数为整数建立方程．

特定项的系数问题及相关参数值的求解等都可依据上述方法求解．

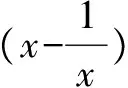
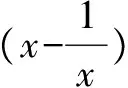
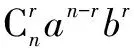
解析本题考查二项式定理，项的系数问题.由二项式展开定理可得其通项为：

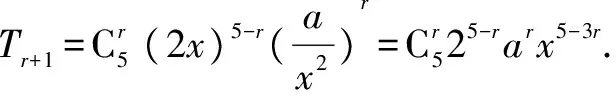
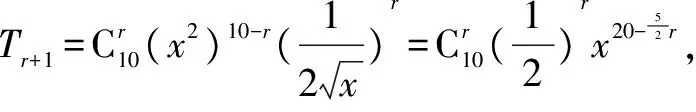
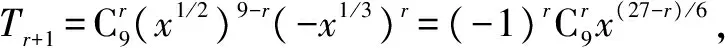
二、系数配对法，理清思路，心无旁骛

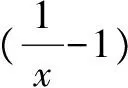
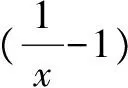
评注“多项式乘以二项式”型的二项式问题，通用的解法是系数配对法，即将多项式中的每一项xk的系数与后面二项式展开式中xr-k的系数相乘，然后把所有这些满足条件的情况相加，即得到xr项的系数．

变式1 (x+2)10(x2-1)的展开式中x10的系数为____(用数字作答).

变式2 (1-ax)2(1+x)6的展开式中，x3项的系数为-16，则实数a的值为____．

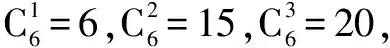
三、组合消项法，化难为易，别有洞天

例3 (2015全国新课标1卷理科第10题)

在(x2+x+y)5的展开式中，x5y2的系数为( )．

A．10 B.2O C.30 D.60

解析化三项为两项，求指定项的系数.

评注在高考中，常常涉及一些多项式二项式问题，主要考查学生的化归能力．归纳起来常见的命题角度有：

(1)几个多项式和的展开式中的特定项(系数)问题：只需依据二项展开式的通项，从每一项中分别得到特定的项，再求和即可．

(2)几个多项式积的展开式中的特定项(系数)问题：一般都可以根据因式连乘的规律，结合组合思想求解，但要注意适当地运用分类方法，以免重复或遗漏．

(3)三项展开式中的特定项(系数)问题：一般先变形化为二项式再解决．

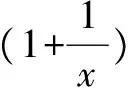
A.1 B.25 C.10 D.252

四、双通项法，双管齐下，有的放矢

A.1 B.25 C.10 D.252

评注先各自独立运用二项展开式的通项公式，再结合题目所求，双管齐下，有的放矢.

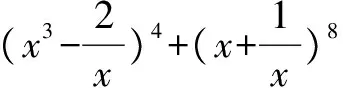
A．32 B．34 C．36 D．38

五、变形代换法，巧妙构造，以小博大

例5 已知1-x+…+(-1)kxk+…+(-1)nxn=a0+a1(x+1)+…+an(x+1)n，其中n∈N*,n≥3．

则当a1+a2=0时，n=____；

当a1-a3=0时，n=____；当a2+a3=0时，n=____．

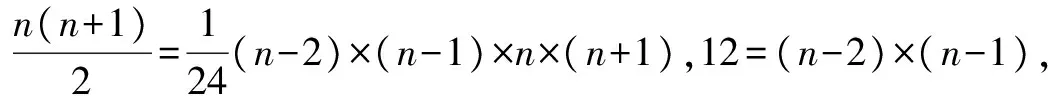
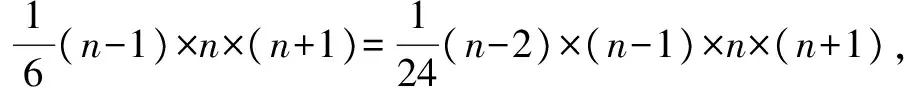
评注变形代换法．在本题中，可将x+1看成一个整体，令t=x+1，再用二项式通项分析法求解．

变式若将函数f(x)=(x-1)5表示为f(x)=a0+a1(x+1)+…+a5(x+1)5，其中a0,a1,…,a5为实数，则a3+a4=____．

六、等比数列求和转化法，转换视角，豁然天开

例6 (1+x)1+(1+x)2+(1+x)3+…+(1+x)2017(x≠0且x≠-1)的展开式中，x1000的系数为( ).

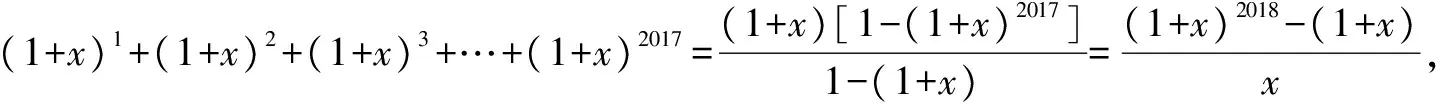
评注根据式子结构特点，把它看成一个等比数列的求和，然后利用公式对其进行化简．

变式1 在(x-1)-(x-1)2+(x-1)3-(x-1)4+(x-1)5的展开式中，x2的系数是____．

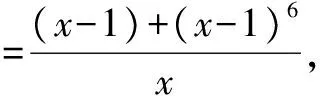
变式2 已知f(x)=(1+x)+(1+x)2+(1+x)3+…+(1+x)2015(x≠0且x≠-1)，则导数f′(x)的展开式中的x1000的系数为( ).

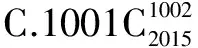
[1] 刘绍学.普通高中课程标准试验教科书·数学选修2-3(必修A版)[M].北京：人民教育出版社，2007.

[2] 王怀学，肖斌.高考数学经典题型与变式[M].拉萨：西藏人民出版社,2016.