(2+1)维扩展Zakharov-Kuznetsov方程的对称、约化和精确解

李会会 刘希强

(聊城大学 数学科学学院,山东 聊城 252059)

0 引言

科学技术的迅速发展, 使得人们对自然现象的了解不断地深入. 许多学者在自然科学与工程技术等许多领域提出了大量具有重要意义的非线性数学模型, 用以描述相关领域的复杂现象. 由于非线性发展方程在工程技术、物理、化学等领域中应用越来越广泛, 而非线性发展方程的精确解在分析各种物理现象中发挥着非常重要的作用, 因此非线性发展方程的求解就成为了数学家和物理学家研究的重要课题之一. 经过众多学者多年研究, 已经发展了许多不同的有效的求解方法, 例如反散射法[1], Painlevé截断分析方法[2], 指数函数展开法[3,4], 经典李群方法[5,6], Jacobi椭圆函数展开法[7,8], 齐次平衡法[9], tanh函数展开法[10,11], Hirota方法[12], (G′/G)展开方法[13]等. 利用这些方法, 可以得到非线性发展方程丰富的精确解, 如孤立波解、周期解、紧致类解等. 其中, 经典李群方法是研究非线性偏微分方程的有力工具之一. 本文运用经典李群方法对下述扩展Zakharov-Kuznetsov方程进行分析研究

ut+uux+u2ux+uxxx+uxyy=0.

(1)

非线性Zakharov-Kuznetsov (ZK)方程是Korteweg-de-Vries (KdV)方程在二维空间的一种推广形式. KdV方程是荷兰科学家Korteweg及其学生de Vries于1894年提出的, 该方程是用以描述潜水波单向运动的数学模型; 继而Zakharov和Kuznetsov为了描述均匀磁场中由冷离子和热等温电子组成的等离子体弱非线性离子声波, 于1974年提出ZK方程作为相应的物理模型. 文献[14]利用推广的(w/g)展开法, 研究了(2+1)维ZK方程, 得到了单循环孤立子解、三角函数解等; 文献[15]利用改进的Riccati方程映射法, 得到了(2+1)维ZK方程的新显示精确解, 并研究了其特殊孤子结构.

本文主要分为以下几部分: 第1部分, 借助经典李群方法求出方程(1)的李点对称以及群不变解; 第2部分, 通过解特征方程组, 求出了方程(1)的相似约化方程, 并结合幂级数展开法、(G′/G)展开法和Riccati辅助函数法求出一些精确解; 第3部分, 利用得出的对称, 得到了该方程的伴随方程和守恒律; 最后, 对本文做出简要的总结.

1 扩展Zakharov-Kuznetsov方程的对称和群不变解

考虑一个单参数李群的无穷小变换

x→x+εξ(x,y,t,u),
y→y+εη(x,y,t,u),
t→x+ετ(x,y,t,u),
u→x+εφ(x,y,t,u),

其中ε是无穷小参数. 上述变换群的单参数向量场表示为如下形式:

(2)

其中ξ(x,y,t,u),η(x,y,t,u),τ(x,y,t,u),φ(x,y,t,u)是待定的系数函数.

根据李群理论, 若向量场(2)是方程(1)的李点对称, 则V必须满足以下条件

Pr(3)V(Δ)|Δ=0=0,

其中Pr(3)V是V的三阶延拓,且其中Δ=ut+uux+u2ux+uxxx+uxyy.

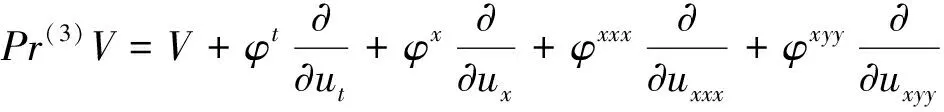
φt+(u+u2)φx+(1+2u)uxφ+uxxx+φxyy=0.

利用李群方法可以得到:

(3)

其中ci(i=1,2,3,4)是任意常数, 由此可得到方程(1)的不变群的生成元为

(4)

同时也能够得到方程(1)的相似对称

(5)

根据李群分析, 方程(1)的所有向量场可以表示为

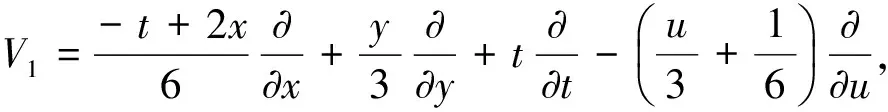
不变群的全体生成元构成一个四维李代数

V1V2V3V4V1016V4-V2-13V3-13V4V2-16V4+V2000V313V3000V413V4000

与它们相应的单参数变换群

g1∶(x,y,t,u)→(x,y,t+ε,u);
g1∶(x,y,t,u)→(x,y+ε,t,u);
g1∶(x,y,t,u)→(x+ε,y,t,u).

由上述单参数不变群可知, 如果u(x,y,t)是方程(1)的解, 则以下u(1),u(2),u(3),u(4)也是方程(1)的解

u(2)=u(x,y,t-ε);
u(3)=u(x,y-ε,t);
u(4)=u(x-ε,y,t);

其中ε是任意常数.

2 扩展Zakharov-Kuznetsov方程的相似约化和精确解

利用方程(1)和σ=0的相容性, 对方程(1)的进行相似约化, 并进一步求得该方程的精确解. 为了获取方程(1)的不变解, 考虑方程(1)对称所对应的特征方程组

(6)

下面分情况讨论

情况1 若c1≠0,c2=c3=c4=0,通过求解相应的特征方程, 可得如下的相似变换

将其代入方程(1)得到相似约化方程

-f+ηfη-ξfξ+3f2fξ+3fξξξ+3fξηη=0.

(7)

首先对上面方程作行波变换f(ξ,η)=f(ω),ω=kξ+lη,并代入(7)式中得

-f+lηf′-kξf′+3kf2f′+3k3f‴+3kl2f‴=0.

对上式进行整理

f‴+k1f2f′-k2ωf′-k2f=0,

(8)

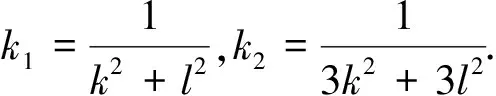
下面利用幂级数展开方法求解方程(8). 假设方程(8)有下述形式的解

(9)

由方程(9), 可以得到

(10)

把方程(10)代入方程(8), 得到

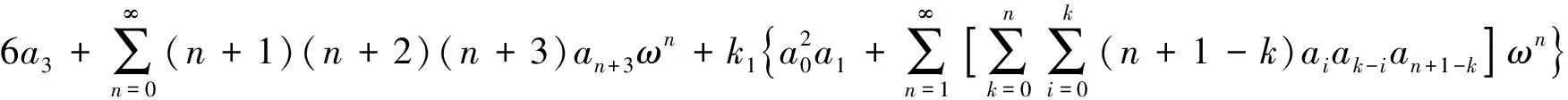
(11)

比较系数, 得到

一般地, 当n≥1时, 可以得到

(12)

事实上, 方程(7)的解为

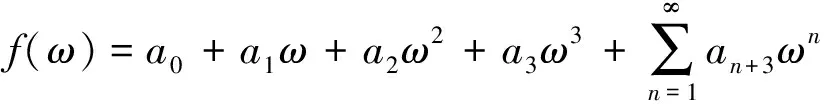
(13)

即可得到方程(1)的精确解.

情况2 若c1=0,c2≠0,c3≠0,c4≠0,通过解相应的特征方程可得

将其代入到方程(1)得到约化方程

(14)

作行波变换f(ξ,η)=f(ω),ω=kξ+lη,并将其代入(14)式中得

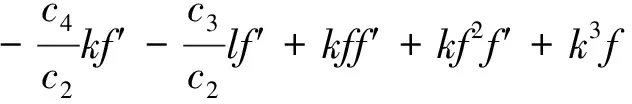
其中k,l是任意非零常数. 对上式关于ω积分一次, 且令积分常数为C得

(15)

为求方程(15)的解, 下面应用(G′/G)展开方法进行求解, 假设方程(15)有如下形式的解

(16)

其中αn≠0,αn为待定常数, 同时G=G(ω)满足G″+λG′+μG=0.

由齐次平衡原理, 可以确定m=1,故方程(15)有如下形式的解

(17)

将(17)式代入(15)式, 同时结合G满足的方程, 合并(G′/G)的各阶偏导数的同次幂项，并令其系数为零, 可得

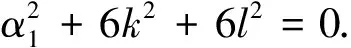
(18)

现在将(17)式的解代入(18)可得到方程(1)的三种形式的行波解:

当λ2-μ>0时

其中C1,C2为任意常数.

若C2=0,此时的u11可以转化为扭结孤立波解

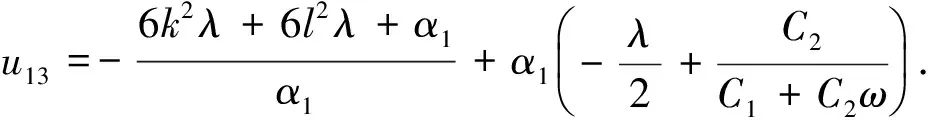
若C2=0,此时的u14可以转化为

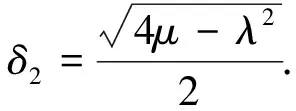
情况3 若c1=c4=0,c2≠0,c3≠0,通过解对应的特征方程,得到

将其代入到方程(1), 得到相似约化方程

(19)

利用Riccati辅助方程求解上式. 作行波变换f(ξ,η)=f(ω),ω=kξ+lη,将其代入到方程(19)中, 得到如下变系数微分方程

(20)

其中k,l是任意常数. 通过平衡方程(20)中最高阶导数项以及非线性项, 可以得到方程(20)应该有如下形式的解：

f=q0+q1Ψ(ω)+q-1Ψ-1(ω),

(21)

其中Ψ=Ψ(ω)满足Riccati辅助方程

Ψ′=h0+h1Ψ+h2Ψ2,

(22)

其中q0,q1,q-1是待定常数,h0,h1,h2是任意常数. 将式(21)、(22)代入式(20), 令Ψ的同次幂项的系数为零, 可得下面四种情况:

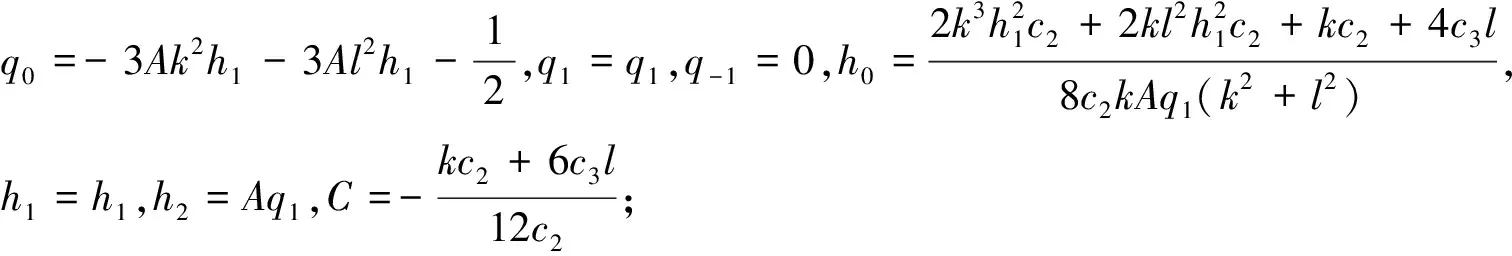
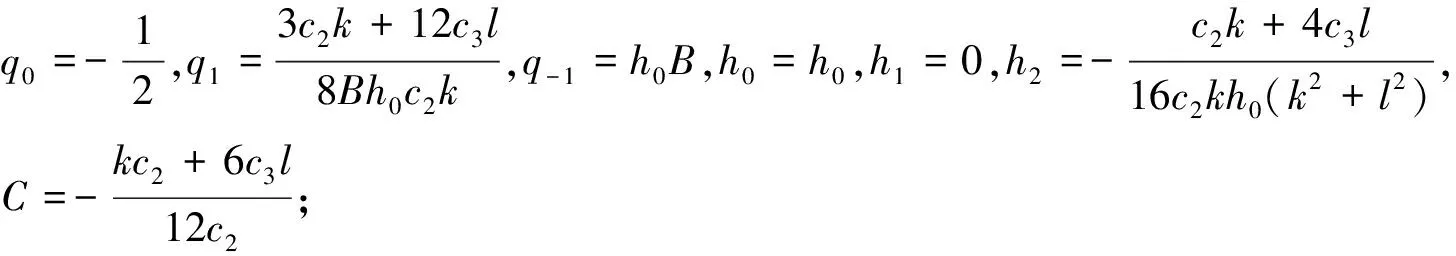
其中A满足(6k2+6l2)A2+1=0;B满足B2+6k2+6l2=0.由此可以得到

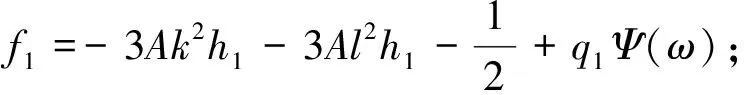
在这里, 我们以第四组数据为例对方程进行求解：

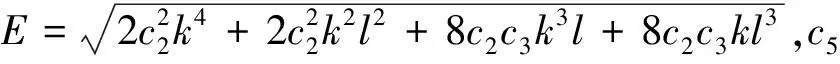
3 扩展Zakharov-Kuznetsov方程的守恒律

守恒律在非线性数学物理科学中有着广泛的应用, 同时它在分析非线性数学物理量的稳定性和存在唯一性起着十分重要的作用. 在这一部分, 利用方程(1)以及对应的伴随方程和对称, 对方程(1)的守恒律进行研究. 方程(1)的共轭方程

vt+uvx+vux+u2vx+2uvux+vxxx+vxyy=0.

(23)

最高阶拉氏量为:

L=v(ut+uux+u2ux+uxxx+uxyy).

(24)

定理1 每个李点对称、李贝克隆变换和方程(1)的对称都给出了扩展的Zakharov-Kuznetsov方程及其共轭方程的一个守恒律,且守恒向量由下式给出

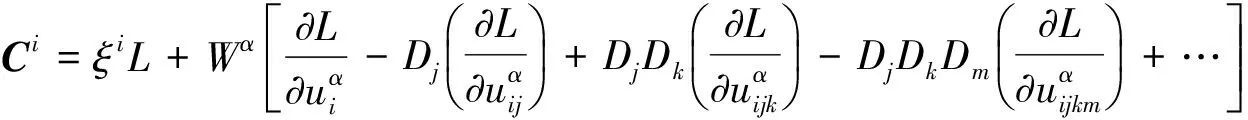
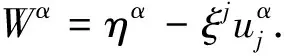
由Ibragimov[16]给出的结论, 方程向量场的通式.

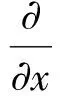
则方程(1)的守恒律将由守恒方程

Dt(C1)+Dx(C2)+Dy(C3)=0

决定, 其中向量场C=(C1,C2,C3)由下面的式子决定

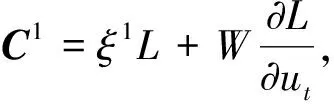
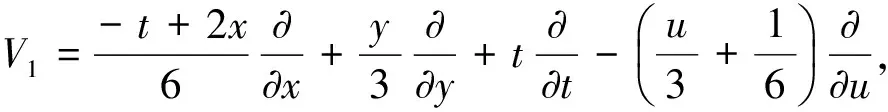
从而

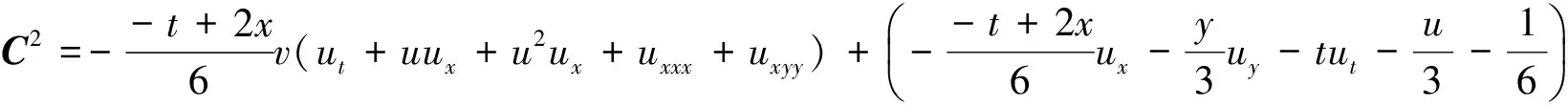
上述守恒向量C=(C1,C2,C3)包含着共轭方程(23)的任意解, 因此以上守恒向量给出了方程(1)的无穷多个守恒律.

4 结论

本文中利用李群方法得到了扩展Zakharov-Kuznetsov方程的对称, 并利用对称得到了该方程的相似约化方程, 将(2+1)维偏微分方程直接约化常微分方程以及(1+1)维偏微分方程. 通过利用齐次平衡法, 再结合幂级数展开法、(G′/G)展开法和Riccati辅助函数法, 求解约化方程, 得到了原方程大量的精确解, 其中有包含幂级数解、行波解等. 这表明这几种方法是实用有效的, 我们以后更应该多加采用. 最后, 利用得到的对称以及共轭方程, 获取了该方程的守恒律.

[1] Aktosun T. Solitons and inverse scattering transform [J]. Contemporary Mathematics, 2005, 379:47.

[2] Hirota R, Satsuma J. Soliton solutions of a coupled Korteweg-de Vries equation[J], Phy Lett A,1981,85:407-408.

[3] He J H, Wu X H. Exp-function method for nonlinear wave equation [J]. Chaos Solitons and Fractals, 2006, 3: 700-708.

[4] Wadati M. Wave propagation in nonlinear lattice II [J]. Phys Soc Jpn, 1975, 38: 681-686.

[5] Chen M, Liu X Q, Wang M. Exact solutions and conservation laws of symmetric regularized long wave equations[J]. Chinese Journal of Quantum Electronics, 2011, 29(1): 21-26.

[6] 田畴. 李群及其在微分方程中的应用[M]. 北京: 科学出版社, 2001.

[7] Zhao X Q, Zhi H Y, Zhang H Q, et al. Improved Jacobi-function method with symbolic computation to construct new double-periodic solutions for the generalized Ito system[J]. Chaos, Solitions and Fractals, 2006, 28(1): 112-126.

[8] Zhang H Q. Extended Jacobi elliptic function expansion method and its applications[J]. Commun Nonlinear Sci Numer Simul, 2007, 12(5): 627-635.

[9] 张辉群. 齐次平衡方法的扩展及应用[J]. 数学物理学报, 2001, 21(3): 321-325.

[10] 李德生, 张鸿庆. 构造孤子方程的Weierstrass 椭圆函数解的一个新方法[J]. 物理学报, 2005, 54(12): 5540-5543.

[11] Wazwaz A M. The extended tanh method for the Zakharov-Kuznetsov (ZK) equation, the modified ZK equation, and its generalized forms[J]. Commun Nonlinear Sci Numer Simul, 2008, 13(16): 1 039-1 047.

[12] Hriota R, Satsuma J. A variety of nonlinear network equations generated from the Bäcklund transformation for the Toda lattice[J]. Progress of Theoretical Physics Supplement, 1975, 59: 64-100.

[13] Wang M L, Li X Z, Zhang J. The(G′/G) expansion method and travelling solutions of nonlinear evolution equations in mathematical physics[J]. Physics Letters A, 2008, 372(4):417-423.

[14] 王振立, 李康. (w/g)展开法求解(2+1)维ZK方程的显示解[J]. 聊城大学学报: 自然科学版, 2014, 27(2): 13-17.

[15] 杨征, 马松华, 方建平.(2+1)维Zakharov-Kuznetsov方程的精确解和孤子结构[J]. 物理学报, 2011, 60(4):92-96.

[16] Ibragimov N H. A new conservation theorem[J]. Journal of Mathematical Analysis Applications, 2007, 333(1):311-328.