基于GARCH模型的股票指数收益率波动性分析

徐旭初 杨 宁

(安徽财经大学 金融学院，安徽 蚌埠 233000)

0 引言

进入21世纪以来，我国股票市场取得了长足的发展，但依然还很不完善.与西方发达国家股票市场相比，我国股票市场的风险和波动程度都很大，股票价格容易被很多因素所影响，这给我国尚不成熟的股市和投资者会带来很大的风险.因此有没有一种可以真实反映股票市场收益率波动性的模型是很多业内学者和大众投资者共同关心的问题.在很多情况下，学者们会利用股票价格指数来研究股票收益率的波动性，主要采用随机游走和ARMA模型.然而近些年来金融市场的变化日新月异，影响股价的因素逐渐增多，传统的ARMA模型已经不能很好的描述其波动性.在这种情况下，产生了ARCH模型，尤其是经过发展的GARCH模型，不仅反映了经济与非经济因素对股票收益率的影响的非对称性，而且在研究股票市场的不确定性和收益率的关系上也有显著的作用，这对投资者的投资选择有很大的帮助.

在国内外研究股票市场的文献中，较为经典的理论中，一个重要的假设就是其中的股票收益率与随机误差项是不相关的，且各自的方差保持不变.当然，在不断发展的经济面前，金融理论也是逐渐进步发展的，随着实证研究的深入，学者们发现股价时刻都在发生变化，且波动具有聚类性，这就类似于平静湖面上的泛起的涟漪，在一次剧烈波动后，下一次波动依然受上一次波动的影响，波动幅度也会偏大，且这种波动带来的方差也会出现偏离一致的现象.在股票市场的数据研究分析中，最经典的就是ARCH(自回归条件异方差模型)模型，这是由Engle[1]提出的，这个模型能够描述在时间不断变化时，市场内股价的变化，这种方法被迅速普及并用于处理金融类数据.之后， Bollerslev[2]在此基础上进行改进，提出GARCH(广义自回归条件异方差)模型，二者的不同点在于GARCH模型说明了观测值的误差具有时变性.但对于金融数据中波动的非对称性并未作出解释，不能体现出坏消息对股市影响的效果大于好消息的.目前，很多学者对我国股票市场进行模型论证.其中，丁华[3]建立了两个ARCH 模型来分析我国上海证交所A股指数的波动性.王耀[4]则在对比了ARCH模型之后，更倾向于GARCH模型，认为后者更能说明问题.杨洲木、门可佩、李俊[5]通过GARCH-M模型针对上海证交所与深圳证交所的数据进行对比，说明了我国股票价格波动大但收益不高的原因.陈艳，韩立磊[6]利用ARCH族模型对上海证交所与深圳证交所的数据进行分析后，发现其有有较为显著的丛聚性和持续性.

通过文献研究发现，GARCH 模型对无条件波动预测较为准确，通过GARCH族能够有效的模拟我国沪深股票指数收益率的波动性，能够帮助那些投资的人在投资过程中准确地把握投资风险，在关键点处进行重要的投资决策.同时，作为投资分析的重要手段，GARCH模型对于我国金融改革也有着重要影响.

1 理论模型

学者们在研究股票市场的最初级阶段，为了研究简化股票市场的波动，形成一个较为完整地理论体系，在假定各股的收益率方差是恒定不变同时，又限定了它们的扰动项互不干扰.但是，这种完美的股票市场是不可能存在于现实之中.随着股票市场理论研究的深入，学者们发现股票市场是瞬息万变的，股票价格的波动变得越发难以琢磨.由于投资者具有很强的从众心理，使得股票价格的波动带有明显的聚集性，它们的扰动项不是互相独立，各股的波动方差也不是恒定的.前期基于这两点假设的关于股票市场波动的模型已经不具有说服力，后继的学者们转而寻找新的解决方案.经过众多学者的理论和实践研究，GARCH类模型在研究股票市场的波动时变性中脱颖而出，在波动的方差开始变化和随机扰动项具有相关关系的前提下，依旧能够很好的解释现实问题，下面对它们进行一些介绍.

1.1 ARCH模型

Engle在做实证分析的时候，创造性的假定t的的方差受到前一刻平方误差干扰，波动的方差恒定不变的假设就此打破，他基于此点率先提出了ARCH模型.

ARCH(p)模型的定义有(1)、(2)方程构成

yt=βxt+εt,

(1)

(2)

其中Ωt-1， 表示t-1时刻的所有有效信息，ht为条件方差.方程(2)表示误差项εt的方差ht的构成包括一个常数项和前p个时刻关于变化量的信息，其中后者用前p个时刻的残差平方表示(ARCH项).

ARCH模型的优点在于：可以很好的反映出金融时间序列波动性的变化，能让投资者对风险的认知和把握能力更强，因而此模型应用较为广泛.但是ARCH模型存在的一个问题，它的前提条件是市场的任何冲击对波动性的反映程度相同，而在实际中，这种反应并不完全相同.

1.2 GARCH模型

在Engle研究的基础上，Bollerslev做出了进一步的改进.他发现ARCH模型在描述序列的尾部分布特征时不够精确，他基于此点提出了ARCH模型的改进版-GARCH模型.广义自回归条件异方差GARCH(p,q)模型可表示为

yt=βxt+εt,

(3)

(4)

其中p是ARCH项的阶数，q是自回归GARCH项的阶数，α>0，β>0.一般认为当ARCH模型中的参数p比较大时，应考虑GARCH 模型，这样更具有说服力.

GARCH模型是ARCH模型的演变形式，它不仅具有ARCH模型的一般优点，而且具有更强的适用性.与ARCH模型相比，由于GARCH模型中没有对参数有任何限制性条件，所以其求解过程较为简单.另外，当样本容量不是很大时，GARCH模型体现了高阶ARCH函数的优越性，有更广泛的使用范围.

2 数据来源与处理

2.1 收益率数据生成

数据采用的是2008年1月7日至2015年12月30日的上证指数与深证指数，共2 940个数据.通过收集到的数据，我们检验之后可得出：在2008年年初到2015年年末，上海股市收益率平均值是0.030 3%，标准差是1.61%，偏度和左偏峰度分别是-0.28、6.78，这比正态分布的峰度值3大很多，体现了收益率rt尖峰厚尾的表现形式.而且，这一点也在正态性检验中体现，在样本容量是2 940的情况下，收益率rt的分布和正态分布也不同.再来看深市收益率的情况，其标准差是1.80%，收益率均值是0.047 9%，偏度和左偏峰度分别是-0.26、5.77，尖峰厚尾的现象也出现在收益率rt中[7].值得注意的是，沪市收益率的标准差更小，说明上海股市的波动更加平稳，深市则反之.

2.2 自相关性检验

使用EVIEWS软件，对上证收益率(RH)序列与深证收益率(RZ)序列分别进行单位根检验.当最优滞后阶数为4时，得到以下的检验结果.

表1上证股票收益率单位根检验结果

t⁃StatisticProb∗AugmentedDickey⁃Fullerteststatistic-23．09470．0000Testcriticalvalues1%level-3．4323885%level-2．86232610%level-2．567233

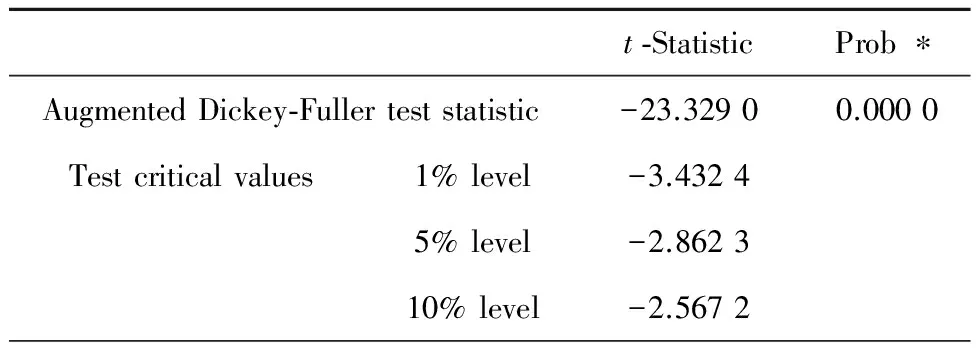
表2 深证股票收益率单位根检验结果

从单位根检验的结果来看，可以看出上证股票收益率、深证股票收益率在1%、5%和10%的显著性水平下单位根检验的的ADF统计量都远远小于其临界值，它们的t检验统计量值分别为-23.094 7，-23.329 0，p值几乎为0，说明上证收益率、深证收益率有单位根的概率接近0，因此认为即使金融资产价格是非平稳的，但是其收益率序列是平稳的[8].

3 实证分析

3.1 GARCH模型建立

同样可以发现，类聚性存在于深市的GARCH模型结果中.因此，GARCH项在两市收益率条件方差方程中都表现出了高度的显著性，其条件方差出现了均值回复过程，也就是历史数据对将来数据的影响是慢慢减小的.从这个模型中，我们可以得出:GARCH效应显著的存在于沪深股市收益率当中；其次，未来数据受到历史数据的影响是逐渐变小，但衰减速度较慢.

3.2 E-GARCH模型的建立

为了研究沪深市场股票收益率对不同方向信息反映不同，我们引入EGARCH模型来解释.首先我们假设a：深证指数收益率的波动不受上证指数收益率的影响；b：上证指数收益率的波动不受深证指数收益率的影响.

利用EVIEWS软件估计模型得到的结果是

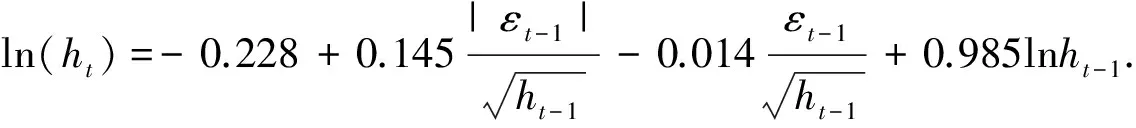
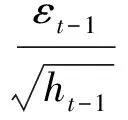
可以看出当沪市的εt-1>0时，冲击倍数为0.149-0.009=0.14.当εt-1<0时，冲击倍数为0.149+0.009=0.158.它们之间相差12%.而深市相差19%.由此我们能得出深市的杠杆效应比沪市的更加显著的结论，即好坏消息对收益率影响的不对称性，对于深市来讲这种非对称性更加明显.

通过EVIEWS软件分别对深沪股市GARCH-M模型中的残差项进行因果性检验得表3

表3 深沪股市残差项检验图

由表3可知，在5%的置信度下，原假设a是成立的：深证指数收益率的波动不受上证指数收益率的影响.但是原假设b不成立：上证指数收益率的波动不受深证指数收益率的影响.这就说明了沪深股市的波动不是完全独立而是呈单向影响的特点，深市的波动对沪市的波动有明显的影响.

4 结论和政策建议

4.1 结论

通过采用GARCH类模型，我们对上证指数与深证指数的一系列特点如：波动性、波动的相互影响和这种影响的不对称做了深入的分析，最后得出的结论：第一，GARCH效应显著的存在于沪深股市收益率当中[10].第二，E-GARCH效应也存在于沪深股市中，未来数据受到历史数据的影响是逐渐衰减，但衰减速度较慢.第三，沪深市场都存在明显的杠杆效应，反映了我国股市中坏消息的负面影响远远超过好消息的正面影响，且这种不对称性对于深圳市场的影响更加显著.第四，沪深股市之间波动性不是独立的，是深市的收益率波动导致了沪市的波动[11].

4.2 对策建议

如果一个国家的金融市场和股票市场较为发达，那么出现一定收益率波动的现象是正常的，这可以提高证券市场的活力.但是由计量模型分析出的结论我们发现，我国证券市场并不十分发达，尚有一些问题亟待解决，故此提出如下的对策:

(1) 健全信息披露制度.羊群效应是我国证券市场存在的一个显著特点，比如股票市场中捕风捉影式的投资时时存在，即根据所谓的内幕消息一拥而上买进或抛售股票，造成市场价格较为剧烈的波动，这对证券市场的正常发展是很不利的.另外，股票的优化资源配置功能和价值发现功能在市场信息的低效率情况下也不能发挥，这违背了发行股票的本意.健全信息披露制度，就是让证券市场的基本信息被金融市场上的投资主体所了解，从而可以理性投资，充分发挥金融市场的功能，使我国证券市场逐步走向成熟.

(2) 加强证券市场化建设.在供给侧结构性改革背景下，中央提出了经济社会的发展要更多靠市场的力量而不是政府干预，在证券市场上更应如此.目前我国由于资本账户尚未开放，所以政府管制还比较严厉，对市场的干预较多.很多情况下，当证券市场低迷时，政府会发布救市信息，人为的活跃市场，证券市场存在泡沫时，又会发布利空消息挤压泡沫.这种政府干预的行为违背了市场的供求关系，忽视了资本资源配置的作用.政府应当明确的是，其作用在于监管和处罚交易过程中的违法违规行为，为广大投资者创造一个健康有序的交易环境.我国证券市场的发展应该是在政府的监管下，充分发挥市场资源配置自身的优势，促进证券市场良好的发展与建设.

(3) 加强对投资者的理性投资教育.目前我国证券市场中的投资者以散户居多，很多散户缺乏专业的投资知识和技巧，跟风投资较多并且偏好短期利益.由于证券市场中很多期货、期权合约实行的是T+0交易，即一天之内可进行多次买进卖出交易，这增加了市场的风险.所以应加强对投资者理性投资的教育，使他们有理性投资的概念，基于市场实际情况和自己的分析做多或做空证券，避免大规模的“羊群效应”[12].

[1] Engle, Modelling the persistence of conditional variances[J]. Econometric Reviews,1986(5)： 1-50.

[2] Bollerslev, Generalized autoregressive conditional heteroskedasticity[J].Journal of Econometrics, 1986,31(3)：307-327.

[3] 丁华．股价指数波动中的 ARCH 现象[J].数量经济与技术经济研究，1999(9):22-25.

[4] 王耀.GARCH模型在计算上海股市风险价值中的应用研究[J].经济问题探索，2007(8):153-157.

[5] 杨洲木，门可佩，李俊.基于GJR-GARCH模型的上海证券市场实证研究[J].现代商贸，2008, 20(1):76-77.

[6] 陈艳，韩立磊.基于GARCH模型的股票指数收益波动性实证研究[J].金融经济,2009 (14):70-72.

[7] 区文玉. 沪深300股指期货与其标的指数的计量分析[D]. 桂林：广西师范大学，2014.

[8] 方俊韬. GARCH模型预测能力评估[J]. 中国物价,2016(1):58-60.

[9] 田华，曹家和．中国股票市场报酬与波动的 GARCH-M 模型[J].系统工程理论与实践，2003(8):81-86.

[10] 张鑫. 已实现GARCH类模型及其应用[D].重庆：重庆理工大学，2015.

[11] 陈千里．上证指数收益的波动性研究[J].数量经济技术研究,2002(6):122-125.

[12] 梁靖. 基于动态跳跃模型的沪深300指数收益率跳跃行为的研究[D].沈阳：东北大学，2014.