回溯算法在可视化物流配送最优路径规划模拟软件中的应用

高小芳

(泉州信息工程学院 软件工程数字媒体系，福建 泉州 362000)

在物流这个行业中，为了满足一个合适的车辆调度策略就需要有一个合适的配送策略，这样才能确认配送路径是否合理还有有没有优化车辆调度.分发配送的过程中的物品，会有很多问题产生，受最主要影响的有两个：动态因素和静态因素.动态因素主要包括道路建设或者其他道路问题、物品收集问题、交通问题等等.静态因素主要包括网上道路问题、配送中物品问题、车辆运行被限制等等.各种配送过程会受受动态因素或者静态因素影响，因为没有选择最佳配送路费以及货物延迟到达目的地而导致经济方面的重大损失.所以现在物流配送面临的一大难题是缺少一个最佳的最优配送路径.在一般情况下，最短配送路径是分为短距离的路径、短时间的路径和成本最经济这三种[1].

1 国内外研究现状

关于物流配送路径选择的研究在国内外主要包括发展路径选择系统的研究、影响路径选择的问题的研究和最优路径算法的研究这三个方向.但是很多国内和国外学者都在做大量关于最优路径算法的研究，这也是国内外最热门的研究话题.

在国内，朱建荣[2]利用很多的蚁群算法的模拟实验来改进最优路径算法，研究成了解决物流配送路径的问题，一种自适应蚁群算法.王荣彦[9]最优路径选择算法是根据遗传算法，两个不同的是，王荣彦的算法研究了解决道路交通的方法就是用动态路段行程时间函数模型来解决，把这些函数的值叫为道路网络.在国外，Filipec、Skrlec和Krajcar[10]他们解决最优配送路径规划问题是使用遗传算法.他们根据交叉、选择和变异等这些遗传并引入了混合算子操作，然后通过并行操作调整它们的适应度.最后的实验测试结果表明，这种算法和明显的增强了种群进化的质量.最后，实验测试结果检验了这种算法的优点：结果相对稳定且具有收敛速度快等.

2 最优路径算法的分析研究

然而，很少有学者用回溯算法来研究物流配送的最优路径规划问题.

(1) Dijkstra算法：时效性是好的，当道路网络越来越复杂，Dijkstra算法可以找到最优解，但它的搜索速度慢，时间复杂度为O(n2)(其中n为问题规模).

(2)蚁群算法：具有很强的鲁棒性和内在的并行性，容易和很多种算法结合，它搜索最优解的能力很强，但是随着社会发展，问题也会越来越多，那么这种算法也很难比较快地搜索到最优解，而且搜索速度又慢，很容易陷入局部搜索.具体该算法的时间复杂度为O(NC*n2*m)(其中NC为循环次数，n为TSP规模，m为蚂蚁数量).

(3) Floyd算法：此算法很简单而且有效，其时间复杂度为O(n3)(其中n为问题规模).

(4) 回溯法：这种算法特别适合只满足一些条件范围性的搜素，它比较适用于大型动态复杂网络.选择最优搜索是一种通过构建约束函数来提高程序的效率的枚举的尝试方式，这些程序结构清晰，容易解读容易被理解，而且应用范围比较广泛还灵活.虽然时间复杂度大，但在实际问题上，根据实际情况做出不同的选择，其具体的时间复杂度是O(n！)，其中n是问题的大小.

(5) 遗传算法：可以直接操纵结构对象且利用概率优化方法，有固定的全局优化能力与隐藏并行性，但是它不会控制收殓过早的问题因为它的随机搜索方向不够明确，其时间复杂度为O(n*2n)，其中这里的n指的是问题的大小.

(6) A*算法：这种算法可以用于求解局部的最优解，它可用于大的静态网络的最优路径问题.这种算法内存空间小，而且搜索的速度很快.但是也是只能有范围内的确定搜索，当真正面临实际问题的时候它会模糊不定，在整体解决中不好取得最优路径.该算法的时间复杂度为O(bd)(其中b是分支因子，即任何节点的后续节点的最大数目;d是主要目标节点的深度).

由以上算法分析可知，回溯算法是类似枚举的首选搜索方法，不仅程序结构清晰，容易解读，而且应用范围广泛并且灵活.基本思路是：一直往前，直到碰到墙壁才回头.也就是说，从一条路向前走，遇到阻挡墙后遇到回归，选择另一种方式去. 另外，Floyd算法相对其他算法而言，适合用于解决小型方向网络中任意两个节点之间的最优路径，边缘权重为正负，密集图的最佳效果，也被经常用于研究算法的最优路径问题.因此，回溯算法是最适合作物流配送路径寻优算法.

3 可视化最优路径规划模拟软件的设计与实现

可视化最优路径规划模拟软件设计的总体想法是，用户在用户界面中随机选择并自己确认仓库点，当确定了仓库点以及那个分配点以后，根据最优算法可以让用户自行在整个配送过程中的路径和单程部分路径选择来回切换；用户可以选择要不要阻塞，但是有时候阻塞会自己产生一个上限值，在被运行的界面上会显示所有的信息，这里的当前分配点或者整条路径的信息包括：整条路径的长度、需要花费的时间以及车的速度，最终这些操作完成后会返回原来的整条路径模式并且会显示信息.

(1) 物流配送最优路径规划模拟软件设计是根据动态规划法和分段法的思想，扔掉了最短路径算法去让三角旅行商算法完成.根据回溯算法对路径优化算法进行分析，它设计出来的软件会自动生成最佳配送路线从仓库点到每个分配点.和其他最优配送路径算法进行比较，对Floyd算法和回溯算法的设计思想进行了优化和改进.

(2) 需要考虑到物流成本因素，包括在最短的时间和时间的车辆等这些因素，目的是节约车辆成本，减少企业的经济成本，从仓库运到最短路线和最佳时间分配时车辆的返回，求阻塞最佳路径.

(3) 物流配送路径规划模拟软件分为生成装载点的功能和GPS移动终端配送路径的选择这两个扩展功能.扩展装载点包括车辆的存储和单个货物的装载两个功能.车辆运输的多数选择需要物品的分配.单个物件对象的扫描使用手持终端进行扫描并传输需要交付的物件对象.这是模拟物流行业中两种常见的分销业务流程.

3.1 可视化最优路径规划模拟软件的系统分析设计

3.1.1 软件开发目的.建立物流公司存在一些在配送过程中的问题，包括车辆配送问题、路线不合理问题、运输由于各种原因产生资源浪费问题、没办法一起配送问题等.利用回溯算法和Floyd算法进行了物流的最优配送路径算法的改进优化，研发面向中小型物流公司可视化最优路径规划模拟软件.

3.1.2 软件运行环境.物流配送最佳路径规划模拟软件的硬件要求是1.8GHz以上的中央处理器，1G以上内存和超过50G的硬盘; 需要的是 Windows XP或Windows 7操作系统并且预先安装.Net Framework 3.5进行设计和实现.

3.2 软件系统的功能需求

3.2.1 软件系统的功能分析.软件功能它们可以分成下面三个层次.

(a) 高—在软件必须实现功能，用户对相关功能和要求有明确的定义.

(b) 中—会在软件中实现功能，但是用户功能的定义和要求可能是不确定的，不是特定的或低约束的.但是缺少这项功能可能导致用户不满意，所以需求分析应指导用户明确相关功能的具体需求.

(c) 低—在软件应尽可能实现功能，并且按照相关功能的开发进度实现，尽可能提高用户的满意程度.

3.2.2 软件功能需求表.按照软件的三个功能层次，设计出了功能需求表，如表1所示.

表1 物流配送最优路径规划模拟软件功能需求表

3.3 软件系统的架构

物流配送管理系统分为界面服务管理系统(UI层)和数据处理系统(DP层)这两层.物流分配管理系统的结构可分为接口服务管理、数据采集和数据处理输出三个部分.服务接口管理包括管理机制、管理保障机制和绘图按钮，用户数据采集和数据交换管理；在数据处理部分输出的数据采集和处理是主要路径一代；数据采集部分是用来连接UI层和DP层之间的数据交换，读取服务器上的数据.

界面服务管理系统(UI层)中的接口主要负责数据输入输出以及接口管理，还负责管理阻止输入的错误消息，以及接收DP层数据.该系统包括绘图按钮保护管理机制，用户数据采集和数据管理四个部分之间的交流，这管理机制是主要在绘制路径移动管理绘制和重绘图片的；控制保护机制是拿来控制恢复和屏蔽功能的；采集用户数据仓库中数据交换管理是DP层传输和访问相关数据.

数据处理系统(DP层)主要从用户界面层实现数据处理，并把有效的数据传输到用户界面层.该系统由数据中间数据交换、采集与计算和路径处理系统管理这三部分组成.数据采集与计算主要是实现邻接矩阵、路径长度、时间和速度数据的生成.路径处理系统是为了使全局最优路径和阻塞的形成；中间数据交换管理是为了对相关数据的采集和传输到用户界面层的传输.

3.4 可视化模拟软件测试

3.4.1 测试环境.总的来说软件测试环境分为硬件环境测试和软件环境测试这两种.物流配送优化路径规划模拟软件只需要一台单机电脑即可完成，需要为1.8 GHz以上的中央处理器频率的硬件要求，1 G以上的内存以及50 G以上的硬盘就可以.所需的软件操作环境是需要预先安装.Net Framework 3.5在Windows XP或Windows 7操作系统上进行设计和实现.

3.4.2 测试方法.通过现实生活中模拟用户真实情况的一种实验测试，不管是否交通有拥堵，可能的问题有两种：(1) 只有一条边可以进去和出来的情况，它存在一些点但只有单条边的点，如图1.(2) 有很多个点且每个点都在主道上面，如图2.

图1 道路问题1 图2 道路问题2

这些问题都会造成后期很严重的后果，我们解决这个问题的方案是确保每个点有三个发展下限来防止出现问题在阻塞的时候.

3.4.3 测试结果.我们对10个分配派送点进行记录，再选中当中的一个分配派送点当做仓库点，找从仓库点到分配派送点的配送的成本最优路径来检验可视化模拟软件的测试效果.在可视化最优路径规划模拟软件中完成了实验测试，并对下面的软件进行了测试，得到测试运行界面.可视化最优路径规划模拟软件主界菜单包括标识投递点、投件、车辆装载、扫描、复位全部、显示信息和退出选项.

(1) 软件运行界面——路径优化，在软件界面中所确定各配送点的坐标且道路信息也清晰.当V3被选择为仓库点时，分发点变成黄色的时候表示着它已经被访问过，如图3所示.也就是说分配派送完成了.软件界面会显示详细信息在分配过程中，动态路径包括坐标的最优路径和当前路径的排列分布和方向，距离的比较和所需要走或者走过的总距离，车辆的平均车速和所花费的总时间.用户还可以通过可视化最优路径规划模拟软件的“信息显示”这个菜单窗口查看当前路径的所有详细信息.这些信息包括了现实道路分布的路径、现实道路所需要花费的时间和和现实道路估计花费时间以及它们的和.在分配完成后，车辆将返回到仓库点，这时车辆最优路径V3-V4-V5-V6-V7-V8-V9-V10-V0-V1-V2-V3会实现，如图4所示.这是没有拥堵的道路的情况，让分配派送的时间最短，且总距离最短从而达到配送成本的最小值.

图3 动态路径线路图 图4 最优路径线路图

(2) 软件运行时——最佳时间，如图5所示.同样分配任务，路径优化是从最短的总配送路径，和时间最优路径V3-V2-V1-V0-V5-V6-V9-V8-V7-V4-V3这里是最小总配送时间消耗.想到现实生活中的情况，用随机阻塞来模拟道路拥挤，如图6所示.当分配派送的车辆到达分配派送点的时候发现前方有道路拥挤或其他情况，这时软件将根据现实实际情况再生成另一条最优配送路径，并且根据这条路径重新分配.由于道路拥堵，对最优路径V3-V2-V0-V1-V5-V6-V9-V10-V8-V7-V4-V3分配的最终结果，在理想条件下的最优分配路径是不一样的，从图6中可以看出，如果配送总时间比预期的要长，但交货时间已经达到最快，最后也会实现减少损失和成本优化的最终目标.

图5 时间最优路径线路图 图6 随机阻塞时的最优路径线路图

在SQL Server 2008和VS2010开发环境里，用C #语言和SQL语言进行编程且实现，按路线来规划随机生成路线的模拟，知道配送的方向、配送的距离、速度以及所花费的总时间，最后选择十组的进行测试优化，优化路径的结果数据线图生成如下.

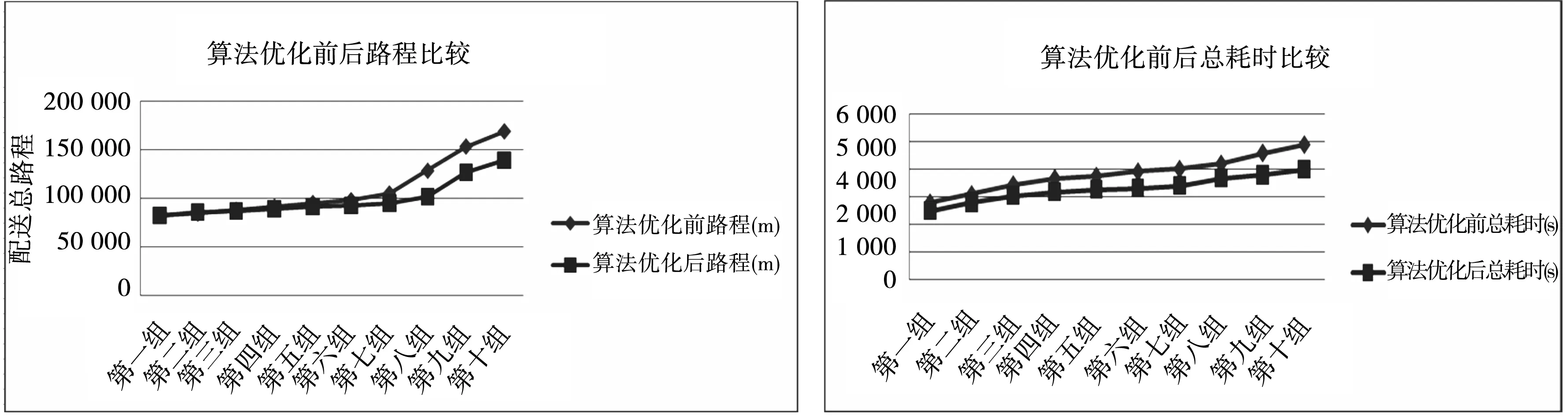
图7 优化前后路程对比数据折线图 图8 优化前后总耗时对比数据折线图

算法优化配送路径的距离，尽管一些组织比以前的配送路径优化长距离从图7可以看出，但选择更不拥挤的配送路程会让交货时间更短，这样能得到更好的配送路径，配送成本也跟着降低，从而更好的满足客户的要求.同时也证实了回溯算法和Floyd算法相结合得到的最优配送路线算法是可以的.从图8可以计算出，之前的数据方差是0.32，优化后的算法方差是0.14，方差算法在优化前的2.3倍左右的优化算法，反映之前不同的离散程度高，同时也表明每条分配路径算法都算比较集中，看到的优化后的每条配送路径优化算法得到的配送总时间也减少很多；在分配派送的时间上，派送路径优化算法根据时间比优化路径那种优化算法的时间长，优化算法的总时间比之前的7%还少一些，由分配派送点的变多，总的时间分布算法的优化是相对减少，即提高分配效率.通过对比图以上数据可以看出，对最优路径算法的优化算法的物流搜索路由与传统路由算法相比，总的路程不短，但是所有时间和是最少的，路径优化算法效率最高，至少从发货到收货时间优化了、最低的成本优化了以及配送路径优化.

4 小结

在整个软件设计过程中的物流配送可视化模拟软件的最优路径规划，尽可能考虑到物流所有成本包括用最短的时间、最近的距离以及路线规划等，这个软件的宗旨是降低成本为各大中小企业节省车辆费用，从仓库到最短路径的每个分布点和时间最优的运输和交通堵塞的车辆后阻塞回溯返回的最优配送路径.首先，按照最优配送路径规划的开发和可视化最优路径规划模拟软件系统运行环境的分析和设计，针对可视化最优路径规划模拟软件系统的功能要求，设计了功能结构图、系统用例图、顺序图和活动图，且提出了可视化最优路径规划模拟软件的总体框架，这个框架主要分为服务管理系统(UI层)和数据处理系统(DP)两个界面，在软件测试完成后，最优路径规划模拟软件已经得到良好的运行效果在路径优化和时间优化这两种不同的分布模式优化.

[1] 姜蕊.融合预测信息的动态路径选择算法研究[D].北京:北京交通大学,2011.

[2] 朱建荣.基于蚁群算法的物流配送车辆优化调度研究[D].长沙:长沙理工大学，2006.

[3] 李军,郭耀煌,物流车辆优化调度理论与方法[M].北京:中国物资出版社,2001.

[4] 包建国.物流网络路径优化及其算法设计[D].哈尔滨:哈尔滨工业大学,2008.

[5] 沈垚.基于改进蚁群算法的配送路线优化研究[D].南京:东南大学,2006.

[6] 王健.现代物流概念的比较研究[J].发展研究,2005(1):59-61.

[7] 中国物流与采购联合会科技信息部. 2012年上半年物流运行情况分析[EB10L]. (2012-07-20)http://www.chinawuliu.com.cn/lhhkx/201207/20/185200.shtml.

[8] 陆琳.不确定信息车辆路径问题及其智能算法研究瞰[M].北京:科学出版社,2010.

[9] 王荣彦.城市交通流诱导系统动态路阻函数及最优路径算法研究[D].西安:长安大学,2008.

[10] Filipec M, Skrlec D, Krajcar S. An efficient implementation of geneticalgorithms for constrained vehicle routing problem[C].//Systems, Man, and Cybernetics,1998 IEEE International Conference,1998(10):2 231-2 236.

[11] 唐彬文,卓雨嘉,陈木芽,等.多点最优组合算法在大学生出游网站中的研究与实现[J].聊城大学学报:自然科学版, 2016,29(4):105-110.

[12] 王勇,池洁.物流配送路线及配送时间的优化分析[J].重庆交通大学学报:自然科学版,2008,27(4):647-650.

[13] 万晓凤,胡伟,方武义,等.基于改进蚁群算法的机器人路径规划研究[J].计算机工程与应用,2014(18):63-66.

[14] 周兴. 面向Internet的动态路径规划算法研究与应用系统设计[D]. 广州：华南理工大学,2011.

[15] 郑烟武. 基于分层分区的动态路径规划算法研究[D].广州：华南理工大学,2011.

[16] 王晓云,陈业纲.计算机算法设计、分析与实现[M].北京:科学出版社,2012.