基于Black-Scholes模型分级基金定价方法的实证分析

濮明月 陈若男

(1.安徽新华学院 教务处,安徽 合肥 230088；2.安徽新华学院 财会与金融学院，安徽 合肥 230088)

0 前言

分级基金是当前一种创新性产品，具有基本的基金结构，将基金运营盈利途径和子份额相互对应作为核心理念，所承担风险等级也有所差异.在功能性及设计方面，分级基金产品明显优于传统类型的基金产品，并且拥有特定的结构划分方法，各项特征比较特殊，包括优先类份额盈利机制、杠杆特点、配对转换机制等.

在分级基金定价方法方面，当前主要应用的是蒙特卡洛、Black-Scholes期权定价模型等方式.张英隽、苟莹[1](2013)学者针对被动型分级基金进行了分析，对子基金加权平均价格、分级基金母基金加权平均净值分别进行了构建，并基于此，对子基金价格、母基金净值二者的协整联系进行了检验，根据大盘指数能够得知大盘指数同上述两项研究内容均具有协整关系，借助Granger因果关系对变量间的动态联系进行表达、检验；张寄洲与邓莹睿[2](2011)等学者基于无套利原理，结合当前国内指数型分级基金定价状况，将银华深证100指数分级基金作为研究对象，借助构建数学模型的方式对偏微分方程进行解答，最终获得显示解，同时还研究了价格同杠杆、参数间的关系；赵贵珺[4](2014)学者深入探究了分级基金定价，在研究过程中运用到蒙特卡罗模拟方式、Black-Scholes方式；此外，在分级基金不定期折算方面，甄君倩[4](2014)学者也开展了分析工作，借助蒙特卡罗法，根据障碍期权定价法，定价了申万菱信深成指分级.由此可见，我国的研究学者主要浅层次的分析了分级基金定价和相关要素，但并未深入探析折价、溢价跟分级基金理论定价的联系，主要研究内容是折价、溢价、实价同基金净值等因素，并未意识到折价、溢价与分级基金理论价格的联系.发行者和投资者分别在对分级基金、投资分级基金进行估值时，必须要明确折价、溢价同分级基金理论估值的联系，这对估值结果有着极大的影响，能够更好的指导估值工作的开展.所以本课题借助研究我国当下市场分级基金产品的途径，在设计过程中，对分级基金关键因素的类型进行划分，并采取逐层放款假设的手段，基于传统定价模型，针对分级基A、B类金份额，研究出新型定价模型，评价、分析各类模型定价的最终结果.

1 Black Scholes期权定价模型

国内在今后会把欧式期权设定成沪深300股指期权，因此在对沪深300股指期权合约定价的过程中，本研究选取了Black Scholes期权定价模型，该定价模型由Robert Merton、Myron Scholes及Fischer Black所构建.

1.1 模型的假设条件

在运用Black Scholes期权定价模型的过程中，存在假设条件，即为：股票价格不断变化；已确定沪深300股指期权短期利率，且该值固定；属于欧式期权，仅可于到期日行使期权；股票无需支付股息，且不分红；存在卖空的现象；资金贷出或借入利率时，不存在风险；期权及股票的交易不涉及费用.

1.2 模型的公式

结合上述假设条件，Black Scholes期权定价模型公式如

c=S0N(d1)-ke-rN(d2),

(1)

p=Ke-r(T-t)N(-d2)-S0N(-d1),

(2)

(3)

(4)

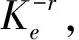
2 波动率参数σ分析

波动率能够体现出股价浮动概率，是研究Black-Scholes模型的关键参数.大波动率就代表股票价格浮动幅度较大的概率很高，就股票价值而言，股票价值不会因波动率的改变而变化.这是由于股票上下浮动的几率相一致，所以二者的作用也会消除.但是基于期权价值层面而言，期权价值会因波动率的变化而改变，期权价值受受股票上下浮动的干扰存在一定的差异.如果股票价格下跌，那么期权费就是投资者(看涨期权)的严重损失，但是如果股票价格相继提高，那么投资收益(看涨期权)也会显著提升.若其余条件均固定，期权价值会随波动率的增大而增大.作为金融工程理论领域的关键参数，波动率的探究还有待进一步的加深.本课题针对Black-Scholes公式，详细研究了两类波动率参数.

2.1 历史波动率

结合市场历史数据，能够对波动率进行运算，可以得到历史波动率这一定价参数.在运算历史波动率的过程中，需要对股票收益率标准差进行运算，首先要对历史股票收益率的平均值进行运算，其次运算平均值同各交易日收益率的差值，之后计算出平方和，求所得数值和交易日期数之商，再减去数值1，运算公式，开平方值就能够运算出历史波动率.

从连续性方面来看，能够将历史波动率划分成离散收益率、连续收益率，具体运算公式表示为

Xi=(Pi-1-Pi)/Pi,

(5)

Xi=in(Pi-1)-in(Pi).

(6)

参考上述不同的运算法，所获取的历史收益率也存在一定差异，这是上述两个公式各自存在相应的假设条件所导致的.其中公式(5)的假设条件为股票价格的变化具有离散不连续的特点，但是公式(6)的假设条件为股票价格的变化具有连续的特点.其与银行利息运算原理相同，在利息预算的过程中既可以选取连续时间复利，也可以将各交易日作为基本单位.本研究借助公式(6)对历史波动率进行运算.

特别要强调，对历史波动率进行运算时，n数值的选取非常重要.就统计学理论而言，精准度会随样本数量的增多而提高，然而历史波动率很容易受时间的干扰，在对今后波动率进行推测的过程中，要保证历史数据不会太久远.所以选择的n值也要做到大小合理.

2.2 隐含波动率

结合期权定价模型运算公式，将各项参数代入其中，能够对波动率的数值进行推导，最终获得的结果即为隐含波动率.市场在推测今后波动的过程中，可以以这些波动率为依据.可以在其余条件下的期权定价模型内，代入波动率数据，得到今后的期权价格.当前市场的风险、期权费有时间价值均涵盖在隐含波动率的范围内.

结合上述分析可知，在对隐含波动进行运算的过程中，要对相关参数进行明确，例如：股票价格、无风险利率及期权执行价格等，同时还要对理论定价模型进行选取，在期权定价模型内替换各项参数数值，即可获得隐含波动率.试错法是计算隐含波动率的关键方式之一，需要对假定波动率数值进行连续的代入，对照分析实际价格同经定价模型运算所得的期权价格是否一致，如果理论价格高于期权价格，就需要对假定波动率进行提升；如果理论价格低于期权价格，应降低假定波动率的值，最终要确保实际价格同理论价格相近.在各项技术快速发展同时，锅动力的运算方式也愈发专业化和高效化，不仅能够采用试错法，也能够借助其他方法进行运算，例如图表法、Newton-Raphson迭代法等等.其中图表法指通过一种直观化的方式，基于文献资料，对隐含波动率进行运算；而Newton-Raphson迭代法指的是，借助计算迭代过程的方式对隐含波动率进行运算.无论从效用层面，还是从实用层面来看，通常都认为今后市场风险能够用假设历史来预测，很多研究人员也将定价参数设定为历史波动率.本课题在研究期权定价问题时，就将理论参数选为历史波动率，代入到Black-Scholes期权定价模型内，从而对随机、常数两大波动率的定价效果进行对照分析.

3 Black-Scholes定价方法特点

当前应用率最高的期权定价模型就是Black-Scholes期权定价模型，其拥有极高的理论价值和意义，正由于此，该模型的创建者荣获了诺贝尔经济学奖.从本质上来看，Black-Scholes期权定价模型理论仍旧停留在浅层次上，以多项假设为前提，但现实和假设存在必然的差异，所以该理论无法同实践生活相联系和整合.

在应用Black-Scholes期权定价模型时，需要将交易成本设定成零，能够以动态的形式不断套期保值，由此验证无风险交易组合理论、风险中性定价理论.然而就实际情况而言，并不存在零交易成本，模型期权价格会因为交易成本在一定区间内浮动，变得不准确.无风险组合也会因交易成本而不成立，这也就不能进行动态不断套期保值，也就不允许风险中性定价的存在.

基于Black-Scholes期权定价模型下，若波动率是特定常数，该假定条件同逻辑思维相违背.借助对股票收益率波动进行模拟的方式，可以确定假定条件不正确，这可以通过上述隐含波动率的分析和研究得知.隐含波动率会由于期权执行价格的差异而出现改变，具有“波动率微笑”的形态特征.此外，隐含波动率在期权到期存在差异的情况下，也具有期限结构，所以可以得知，波动率为随机变量.

借助Black-Scholes期权定价模型进行分析时，要将股价看作是符合电视正态分布的特点，而且是不断变化的，然而在实践中，股价呈跳跃式，具有不连续的特点.结合几何布朗运动，股价的跳跃存在突然性的特点，不能进行准确的描述分析.

同时，在应用Black-Scholes期权定价模型时，需要将标的资产收益、无风险利率均设定成常数，然而在实践中却为不断波动变化的.

不可否认的是，Black-Scholes期权定价模型虽然是通用性较强的模型，却也不够完善，众多研究人员均以该模型为基础，详细探究各项假定的条件.Black-Scholes期权定价模型期权定价理论的重要性不言而喻.本课题基于Black-Scholes期权定价模型，借助对假定条件进行放宽的方式，详细分析分级基金的定价效果.

4 实证分析

4.1 数据选择

在研究中，将瑞和远见(15002)、国投瑞银瑞、瑞和小康(15001)、三百分级基金(161207)与子基金作为定价对象样本，上述基金均属于指数型分级基金.在对样本进行选取的过程中，需要考虑以下因素：分级基金必须是当前市场中具有开放和结构化特征的唯一基金；对应收益分配方式非常独特，且存在代表特征；分级基金的结构化运作具体是，若母基金净值、A份额阈值、B份额阈值均大于1，在10%的范围内，分配收益的比例为8∶2，而在超出10%的范围内，分配收益的比例为2∶8；如果母基金净值比1小，母基金净值、A份额和B份额相一致.瑞和沪深300指数分级基金于2009年9月正式发行，其为国内首个指数型分级基金，具有全新的交易机制和收益特点，收益分配也呈现结构化的特征，构建出一种极具代表性的分级基金.瑞和沪深300指数分级基金同沪深300指数基本相同，瑞和远见和瑞和小康二者仅因为差额分配机制，从而在净值收益年阈值外及阈值内，呈现出不同的杠杆率.结合市场预测两类份额价格的波动状况，投资者能够借助弹性策略，对基金份额进行有效投资

仅单一欧式期权定价适用期权定价法，所以研究分级基金的定价问题时，可以借助期权定价法.第一步，要拆分分级基金的进取类份额、优先类份额，构成存在期权差异的组合，借助模型对单一期权理论价格进行运算；第二步，运用组合方法对A份额和B份额的价格进行运算.进取类份额瑞和远见对应的份额净值、优先类份额瑞和小康对应的份额净值同母基金份额瑞银瑞和300对应的份额净值依次表示成：NAVb、NAVa及NAV.结合基金产品的详细设计规定，针对瑞和沪深300来说，其各类份额对应净值结构为

N≤1,NAV=NAVa=NAVb,
1N≤1.1,NAVa=1+2*0.8*(NAV-1)，

(7)

1N≤1.1,NAVa=1+2*0.8*(NAV-1),
NAVb=1+2*0.2*(NAV-1)=2NAV-NAVa，

(8)

N≻1.1,NAVa=1+2*0.8*0.1+2*(NAV-1.1),
NAVb=1+2*0.2*0.1+2*(NAV-1.1)=2NAV-NAVa.

经过进一步的简化与整合，能够获得公式

NAVa=NAV+0.6max(NAV-1.0)-1.2max(NAV-1.1,0)
NAVb=NAV-0.6max(NAV-1.0)+1.2max(NAV-1.1,0).

结合分析所知，1份国投瑞银瑞和300净值与1.2份看涨期权多头(执行价K是1.1)之差，再加上0.6份看涨期权多头(执行价K是1)，最终结果等于1份瑞和小康价格.

1份国投瑞银瑞和300净值与1.2份看涨期权多头(执行价K是1.1)之和，再减去0.6份看涨期权多头(知心加K是1)，最终结果等于1份瑞和远见价格.

本研究在开展实证分析工作时，就借助了通用的Black-Scholes期权定价模型.

4.2 Black-Scholes模型的建立

本研究针对国投瑞银瑞和300分级基金，在开展实证研究工作的过程中，充分发挥了Black-Scholes期权定价模型的作用.该模型的两大核心参数为无风险利率、波动率.结合上述研究和分析，可以通过运算获得波动率，在随机、常数波动率的定价效果对照研究方面，需要将参数设定为历史波动率，而无风险利率参数则可以设定为Shibor利率(存在于定价区间中).

对于看涨期权价格(不分红)进行运算时，对应的Black-Scholes期权定价模型为

(11)

(12)

(13)

国瑞银瑞和母基金净值是，波动率、无风险利率分别是σ和r，到期日是t，期权执行价格是K.

4.3 价格波动率

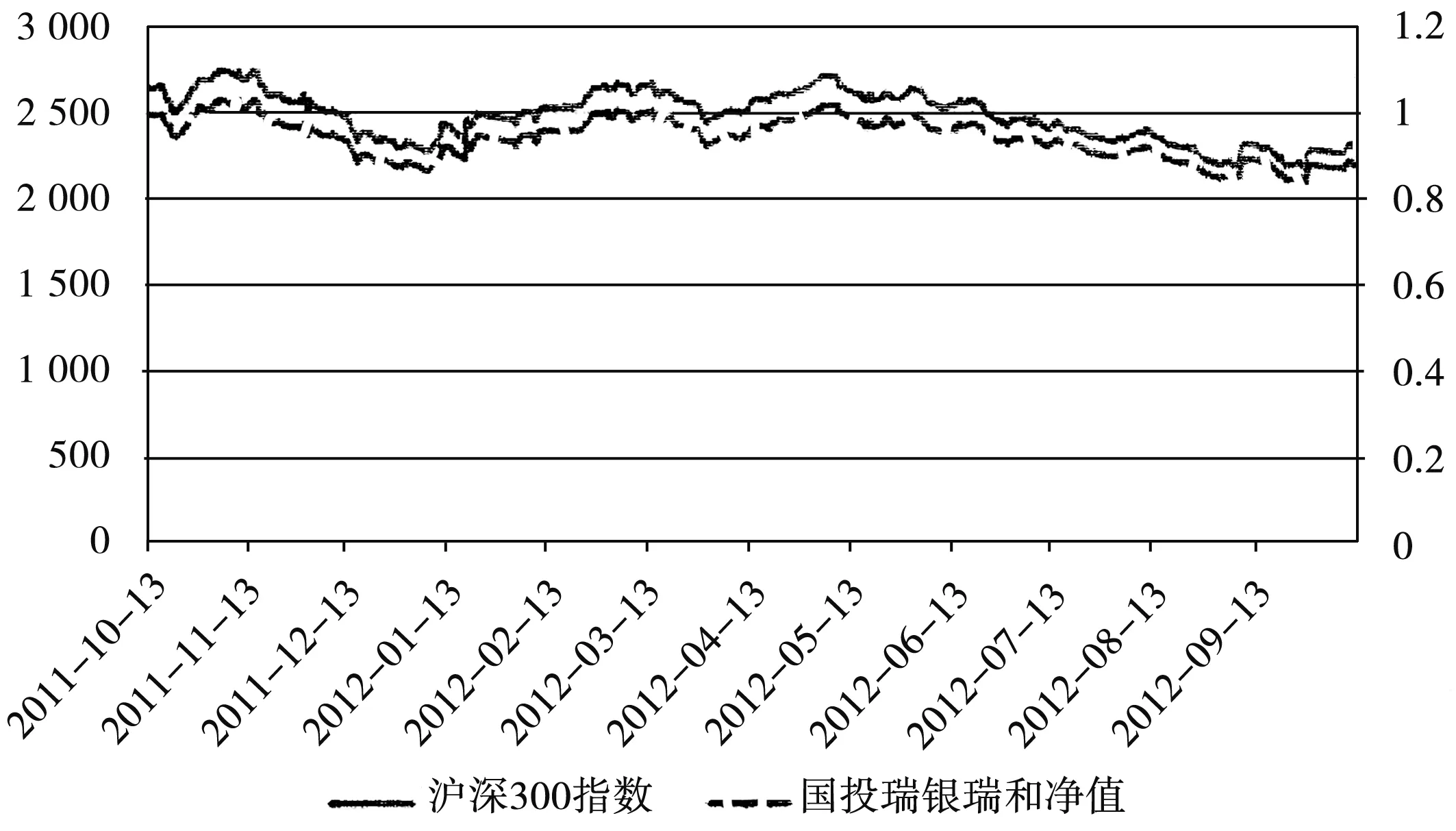
图1 沪深300指数与国投瑞银瑞和300产品走势图

在结构运作模式方面，国投瑞银A份额、B份额非常独特，会随着市场的变化发生同方向的改变，但研究在对波动率进行测度时，要以沪深300指数同期指数为基础，较为准确的拟合波动率.结合当前市场发展状况，沪深300指数标的拥有极强的代表特征，根据走势可以反映出市场波动率.估测上证指数收益率时，或者开展样本外预测工作时，都可以应用GARCH类模型，在推测波动率的过程中，必须要建立在经运算得到的波动率数据的基础上.基于GARCH类模型，在推测波动率时，需要借助损失函数、M-Z回归函数，结果体现出在样本内、外，在对上证指数的收益波动率进行推测时，GARCH类函数发挥着重要的作用(黄海南、钟伟,2007).

在本研究中，将沪深300指数作为产品投资标的，进行Eviews测试后，国投瑞银瑞和净值、沪深300指数二者的高度相关，且相关系数是0.997.结合分析，本研究在对历史波动率这一重要参数进行运算时，根据的主要是是沪深300指数.估计样本的数据是从2011年10月13日起，到次年同月11日止，针对沪深300指数的243个交易日.结合运算公式，能够对年化波动率进行运算，结果是20.41%.

4.4 无风险利率

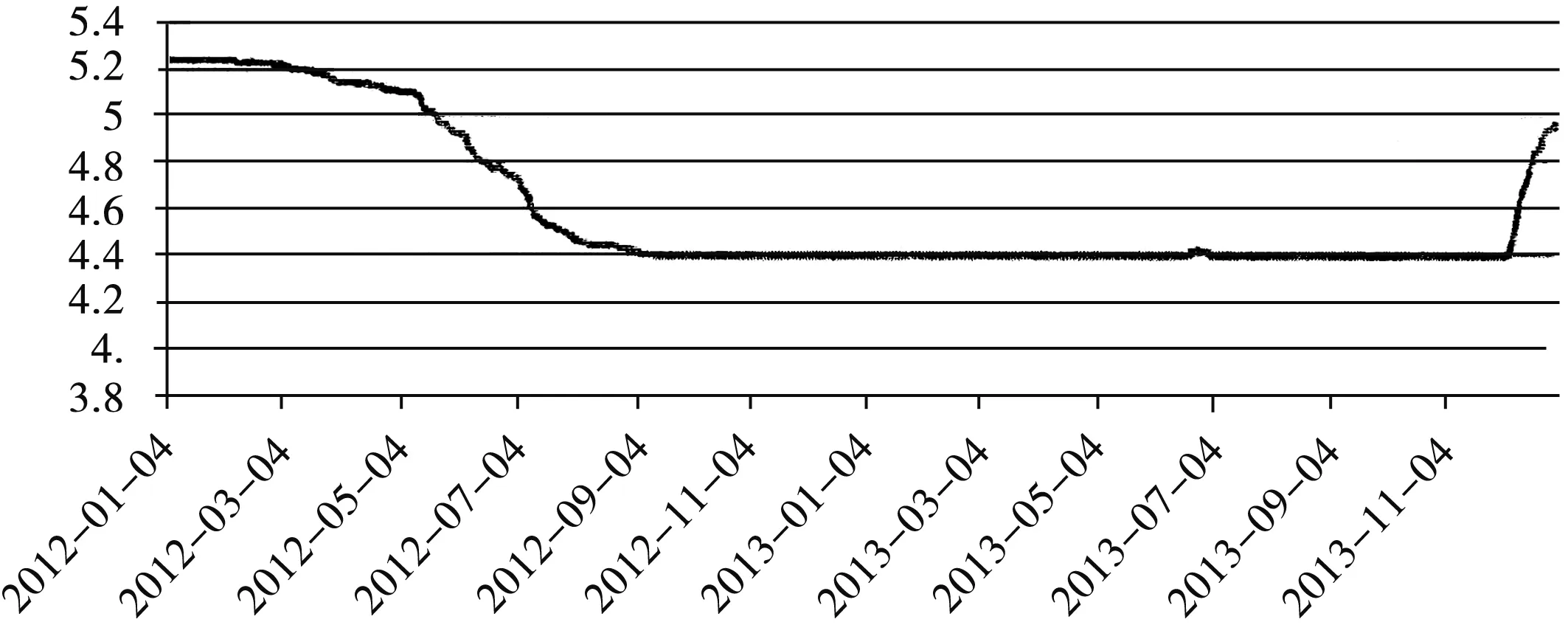
图2 2012-2013年1年期shibor走势图

在运算无风险利率时，主要根据的是相同时间段内分级基金A份额隐含收益率、余额宝一周年化收益率、AAA级无担保债券08江铜债(余下1.24年期限)的期间收益率和相同时间段内上海银行间同业拆借利率，这些理财产品收益率都存在债性特点.这主要是因为配对转换机制是分级基金的一大特征，而且套利的形成是因为二级市场价格、基金净值不统一，且同其余类似理财产品收益率相比，A份额明显不同，这就会导致投资者更加趋向于收益率高的理财产品.针对这些理财产品，在对无风险利率进行运算时或应用到动态因子方差法，能够对无风险收益率的变化状况进行体现，也能够对共同变化成分进行揭示[5].

本研究认为运行时间段内，标的收益率、价格的变化具有随机性的特点，无风险收益率、波动率参数在期权定价模型中的确定，可以选择随机变化的标的，借此从理论上对分级基金的两类份额进行运算.课题选取的上海银行间同业拆放利率是1年期，历史时段的Shibor利率基本不变，详见图2.结合图2显示，从2012年10月12日起，至次年同月10日的定价为止，Shibor变动较小，大概为4.4%，所以将1年期的Shibor设定成无风险利率参数(r)，取值4.4%.

4.5 数据的调整

2009年6月至2015年6月为本课题索取数据的时段，因为国内资本市场于14年6月出现牛市，因此估值时段要选为14年6月到15年6月.其中，需要调整间断数据，使其呈现连续的特点，比如：特殊状况导致的基金停牌、节假日等，这样才能够使研究数据更加完整.

4.6 Black-Scholes模型定价国投瑞银瑞和300分级基金

在明确Black-Scholes模型的前提下，需要结合相应公式，定价国投瑞银远见、国投瑞银小康分级基金.由此获得改模型的定价结果，如图3,图4所示.

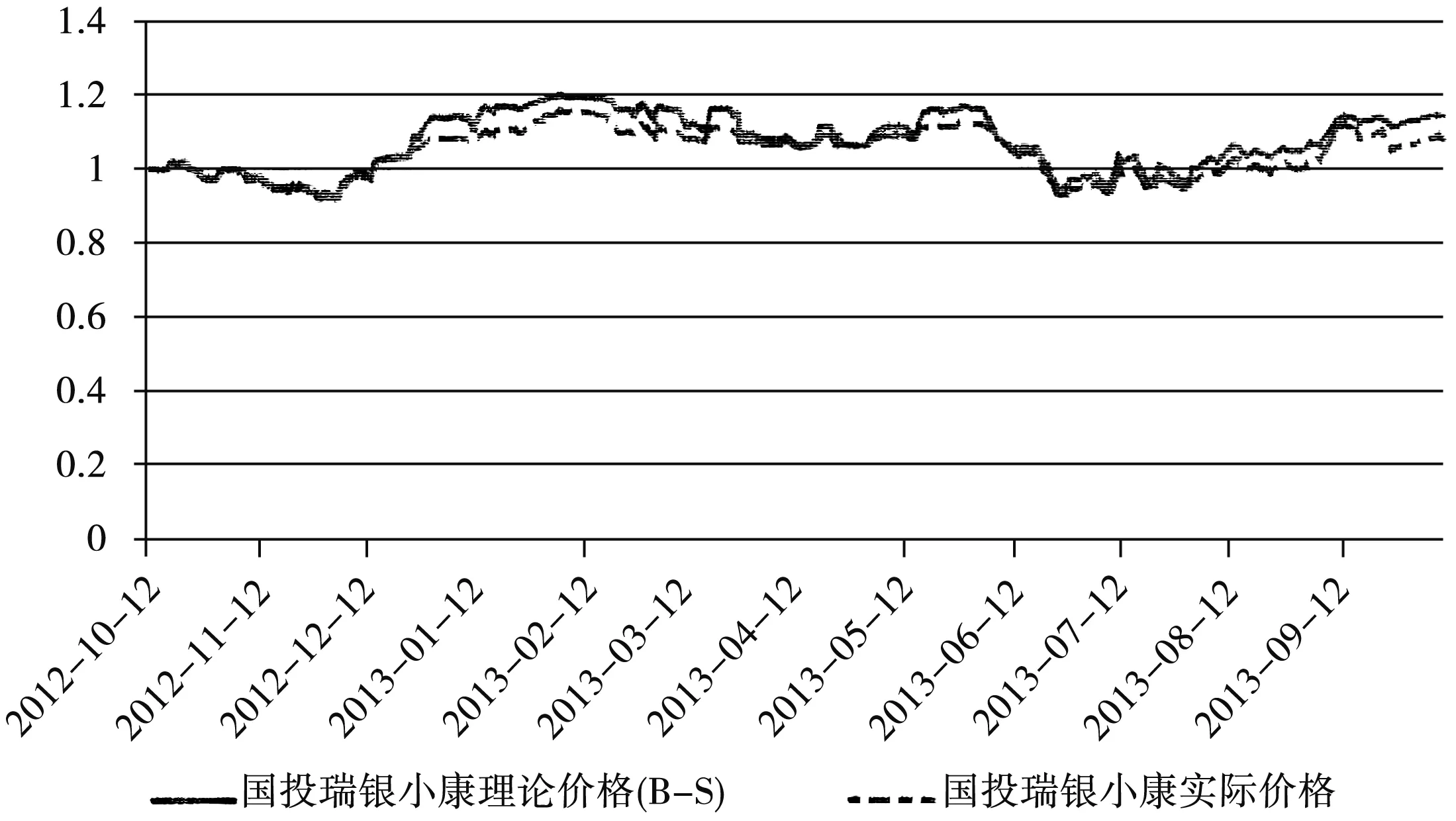
图3 国投瑞银小康理论价格(B-S)和实际价格对比图

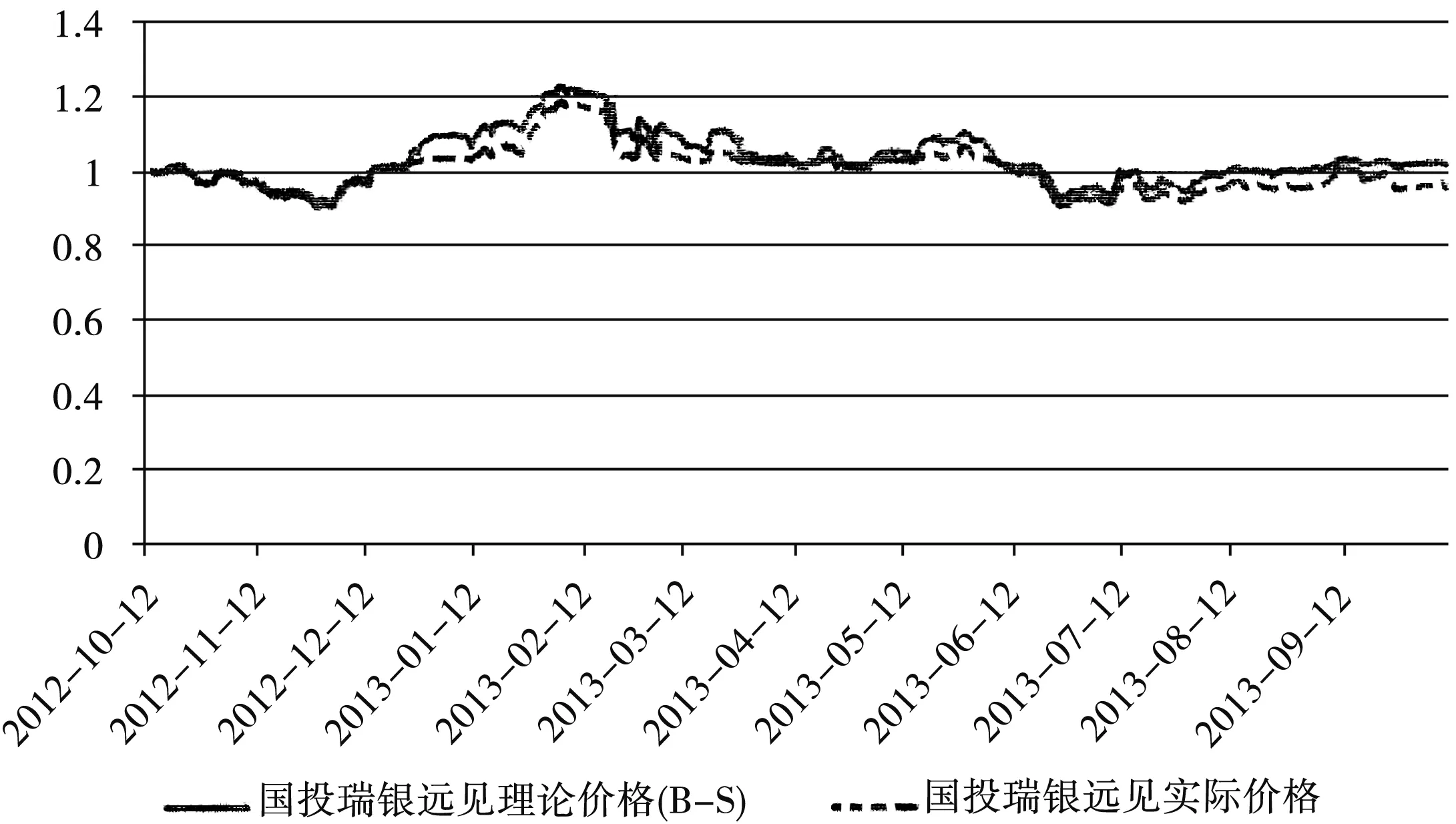
图4 国投瑞银远见理论价格(B-S)和实际价格对比图

结合得知Black-Scholes模型的最终定价结果如：(1) 针对瑞和远见、瑞和小康分级基金，在理论层次的价格发生变化时，二者市场价格的变化趋势一致.(2) 瑞银远见、瑞银小康于2012年12月20日到次年5月31日分别发生较小的折价和溢价，折溢价幅度存在差异.(3) 瑞银远见、瑞银小康于2013年6月1日到10月10日分别发生较小的溢价和折价，折溢价幅度存在差异.体现出市场供需、偏好的改变情况，揭示了基于配对转换机制下，套利可能性的时期较短.

5 结论及展望

基于市场各时期经济净值、市场价格及分级基金理论价格明显不同：在上行时期，分级基金子份额超出阈值范围后，三者的价格变动方向差异较大；投资者会受到分级基金母基金的理论价格同分级基金母基金折价率、母基金溢价率负相关联系的影响，结合格兰杰因果关系得知，折价率、溢价率同理论价格于10%及1%的情况下会彼此产生影响，前两者的改变会严重影响理论估值.本研究认为分级基金折溢价率在很大程度上受资者情绪的干扰，能够负面影响理论价格.

[1] 苟莹, 孙英隽. 我国分级基金价格、净值和大盘指数的实证分析[J]. 中国集体经济, 2013(15):47-48.

[2] 王杨,邓莹睿,张寄洲.中国市场上一类指数型分级基金的定价模型与金融分析[J].上海金融学院学报,2011(6): 32-42.

[3] 赵贵珺.中国市场一类指数型股票分级基金定价方法研究[D]. 成都：西南财经大学, 2014.

[4] 甄君倩.中国股票被动型分级基金定价研究[D]. 上海：复旦大学, 2014.

[5] 吴恒煜,陈金贤,赵平.我国商业银行操作风险的博弈分析[J].西安交通大学学报,2009, 29(3):19-23.