从“学程前总结”的角度谈课堂导入的常见误区

徐小建（江苏省南通市通州区平潮实验初中）

从“学程前总结”的角度谈课堂导入的常见误区

徐小建（江苏省南通市通州区平潮实验初中）

通过对若干典型案例的研究，梳理出课堂导入过程中低效化、复杂化、简单化、幼稚化、碎片化、自发化等六种常见误区，并从学程前总结的角度对误区的形成原因进行了剖析.

最近发展区；课堂导入；常见误区

一、学程前总结的内涵

所谓学程前总结，是指在新学程开始时激活学生原有的认知，调动学生的学习情绪，使相关认知模块处于被激发，相关信息通道处于双向开放的状态，为新知的产生、生长做好必要准备的过程，也就是将学生引入“最近发展区”的过程.也许有人要说，这不就是课堂导入吗？事实上，在这里为什么要说成是学程前总结而不说成是课堂导入是有原因的．因为导入的本质是对外来的引进，最高境界就是融合、生长，而总结的本质是指内部的主动生长，不是外来的嫁接，更不是直接的告知，是自主生长，种子是原本就根植于学生心中的.教师的作用就在于再次激活学生内心原有认知的生长点，为了激活这个生长点，就必须对学生已有的认知进行梳理、总结.而在实际教学过程中，一些教师对学程前总结的理解存在着不少误区，一味强调导入，甚至有时就是植入．下面通过几个案例来谈谈笔者的认识.

二、从学程前总结的角度对课堂导入常见误区的剖析

1.忽视学生已有认知，使教学过程低效化

学程前总结认为，任何学习都不是孤立的过程，它是建立在学生已有认知基础上再学习、再建构、循环往复的过程.因此，从学程前总结的角度来说，了解学生的已有认知是课堂导入的必修课，必须在课前对学生的认知有足够深入的了解，做到知己知彼，而不是凭着教师主观的经验去猜测学生的学情．然而在实际教学过程中，由于有教师对学生已有知识和能力把握不准，常常主观推测学生的认知基础，在教学过程中常常会出现教学起点低于或高于学生的已有认知的情况，前者导致低效重复，后者导致高不可攀.这两种情况都会导致内容混乱、效率低下.

案例1：“平行四边形的性质（第1课时）”之平行四边形概念引入片断.

师：同学们，现在请拿出准备好的如图1所示的两个全等的三角形纸片，用这两个三角形的纸片来做一个拼图游戏，看看我们能拼出哪些四边形？

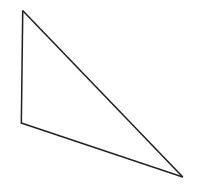
图1

学生拼图，并小组交流，3分钟后教师让小组代表展示成果.

生1：我们小组共拼出了如图2～7所示的6种图形.

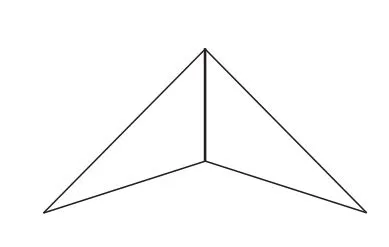
图2

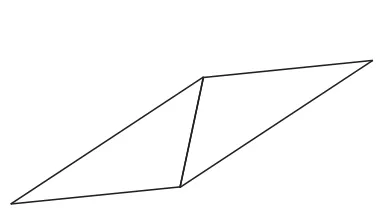
图3

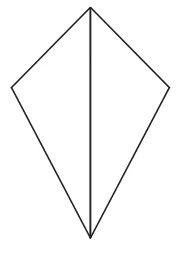
图4

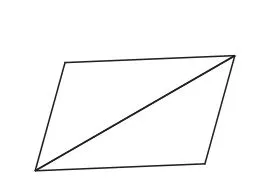
图5

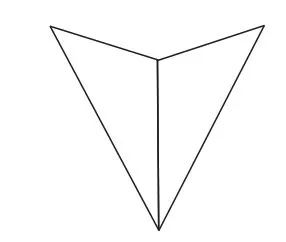
图6

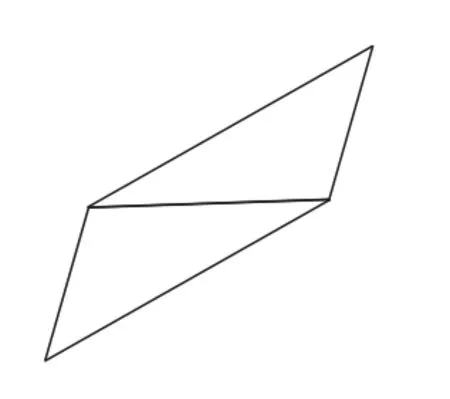
图7

师：非常好，能说说你们是怎么拼的吗？

生1：我们小组是将相等的边拼在一起，然后再巅倒一下，这样能得两个不同的四边形，将三条边都这样拼一下，就有6个四边形了.

师：你说得太好了！下面大家来给这6个四边形分分类，看能分为几类？

学生小组交流，2分钟后，教师让小组代表回报分类情况.

生2：我们小组觉得可分为轴对称的一类，和不轴对称的一类.

师：你来说说哪几个是轴对称的图形，哪几个不是轴对称图形？

生2：图2、图4和图6是轴对称图形，其余不是轴对称的.

师：说得对.有哪个小组有不同的分类方法？

沉默了一会儿，没有小组发言.

师：那我们来看看图3，图5，图7，它们是什么图形呢？

生：平形四边形.

师：为什么是平行四边形呢？

师：那我们今天就来研究什么是平行四边形.

【评析】平行四边形是学生在小学就已经认识了的概念，《义务教育数学课程标准（2011年版）》（以下简称《标准》）第二学段（4～6年级）明确要求学生认识平行四边行.因此，在初中阶段进一步研究平行四边形的性质时，重点不是让学生发现平行四边行，而应是从平行四边形的定义出发，借助平行线和全等三角形的知识去研究有关线段和角的关系.从案例1中可以发现，教师在设计本节课的导入环节时至少有以下几点不当：（1）不了解学生的已有认知基础，一味地从活动入手，试图从活动中引入平行四边形；（2）不了解学生的思维基础，让学生对所拼的6个四边形进行分类，指向不明，与本节课的教学没有明确的关联；（3）不理解判定与性质的关系，导入让人不明白本节课到底是研究性质还是研究判定.其实对于本节课的处理，如果找不到好的情境，不妨开门见山地说：同学们，在小学的时候我们就认识了平行四边形，中学阶段我们将进一步深入研究平行四边形，下面请大家说说你所理解的平行四边形.然后在同学们的畅所欲言中引导学生理解定义，掌握性质，梳理知识结构，渗透研究方法.通过这种直白的引入将学生迅速拉入主题不失为一种高效教学形式.

2.刻意创设标新情境，使教学过程复杂化

学程前总结强调认知的主动生长性，生长就必须营造一个好环境，利用熟悉的情境完成新知的学习和建构．然而，在实际教学过程中，一些教师忽视学生的常规经验，使得教学情境游离于学生的生活，为求新而标新，将简单的问题复杂化，从而导致目标不明、节奏拖沓.

案例2：“平面直角坐标系（第1课时）”之有序数对引入片断简述.

教师通过“幸运52”的形式确定本节课的“幸运之星”，来导入新课，将学生的积极性充分调动起来，然后教师意图引导学生通过抽行号和抽列号的方法得出今天的幸运之星，从而导出有序数对的知识.但是学生总是想不到教师预设的轨道上去，后来总算想到抽签的方法，又由于学生缺乏对抽签这一方法公平性的认知，导致有学生认为先抽签的人占光，最后教师不得不和盘托出用有序数对确定位置的方法，花费了15分钟的时间才引入了课题.

【评析】创设情境的目的是激发学生兴趣，促进学生的思维，引导学生自主发现．若情境设置得过于复杂，对学生来说犹如雾里看花，怎么也看不懂情境中所蕴含的数学内涵，不仅起不到应有的激发与促进作用，只会造成目标不明，节凑拖沓．在本例中所设置的抽幸运之星的情境，由于学生想不到用抽列号与行号的办法来产生幸运之星，而教师无意中提到的公平性却成了学生感兴趣的话题，使得宝贵的课堂时间被白白浪费在与本节课无关的细枝末节上，导致本节课的主要内容——有序数对，千呼万唤出不来，最后教师不得不和盘托出．事实上，对于这类问题，如果用教材中的学生在教室中的位置、电影院中的座位等经典情境引入新课更简洁明了，直指目标.

3.忽视发展学生思维，使发现过程简单化

学程前总结强调认知的主动生长性，课堂导入应成为一个催芽的过程，而不是一个播种、嫁接的过程．而在实际教学中，一些教师为了所谓的高效、高分，确保课堂教学的顺利进行，而减少了教学过程中思维的力度，刻意降低发现的门槛，剥夺学生发现的权利，用虚假的繁荣掩盖思维的贫乏.

案例3：感知根与系数的关系简述.

教师通过几个具体的方程，让学生分别求出方程的两个根x1和x2，并填入相应的表中，然后让学生计算x1＋x2和x1x2的值，再让学生将x1＋x2和x1x2的值和方程的系数进行对比，猜想出一般性的结论，最后用字母系数的方程进行了结论的证明.

【评析】对于案例3的做法，该教师认为这一设计让学生经历了由特殊到一般，由具体到抽象的过程，有利于学生对所学知识的理解.这一点，笔者表示认可.但是，对于根与系数关系的探究过程中的两个难点，即为什么要研究根与系数的关系和如何研究根与系数的关系，在上述探究过程中均以填表的形式被轻以突破，学生的收获只能是“是什么”而不是“为什么”.对于根与系数关系的探究，笔者在实际教学过程中常增加一步探索发现的过程，还学生发现的权利和机会，在探究之后再通过类似案例3的方法让学生进行验证、证明，这样让学生有自主发现、提出问题的机会，同时又能有效保障学困生获得最基本的技能.

下面笔者给出探究根与系数关系第一步的简略设计过程.

案例4：探究根与系数的关系.

已知一元二次方程ax2＋bx＋c＝0（a≠0，a，b，c为常数），当b2－4ac≥0时，两个实数根分别为x1＝

观察上述一元二次方程的求根公式，思考以下问题.

（1）一元二次方程的两个根在表达式上有什么异同？

（2）一元二次方程的求根公式揭示了一元二次方程的每一个根与系数之间的关系，这个关系看上去还是比较复杂的.那么，联想刚才对两根异同的比较，我们能否寻找到一元二次方程的两个根与三个系数之间的更为简洁的关系式呢？

4.一味强调操作实验，使规律揭示幼稚化

在数学教学过程中，必要的操作实验可增加学生的感性认识，为上升到理性认识打下必要的物质基础.但是，对于那些学生已有一定理性认知基础的知识，如果再退回到让学生操作、观察等初级阶段，则是一种思维的倒退，轻则弱化了数学的思想方法，重则会强化错误认识.这一做法也违背了学程前总结所提出的基于学生已有认知生长的主张．

案例5：“单项式与单项式相乘”教学片断简述.

活动1：拼一拼.用6张长为a、宽为b的长方形纸片，拼成一个大长方形，尽可能多的展示不同的拼法.

接着教师让学生用不同的方法表示长方形的面积，再根据面积相等得出3a·2b=6ab，类似地得出2a·4b＝8ab；

活动2：说一说．让学生说出依据是乘法的交换律．

活动3：试一试．求底面积为5x2，高为2xy的长方体体积．

活动4：做一做．计算：（1）2a2b·3ab2；（2）4ab2· 5b；（3）6x3·（－2x2y）．

活动5：谈一谈．让学生归纳“单项式×单项式”的乘法运算法则.

该教师认为，这种以“拼、说、试、做、谈”五个活动为载体的教学过程中，拼让学生经历了操作、观察、思考、交流等过程，为学生积累了一些感性认识，并初步理解了“单项式×单项式”的意义，在后面四个环节中将拼的感性认识上升到理性的认识.整个过程关注了学生从感性到理性认识的思维发展规律，真正使教学过程起到授之以渔的作用.

【评析】笔者认为对于案例5中所设计的五个活动有没有必要，是否适合教学实际，能否促进学生的发展，关键要看我们关注的是数学思维的本质还是形式.在“单项式×单项式”的教学过程中，学生的最新知识基础是单项式.在近期的学习中，学生不仅知道了什么是单项式，而且还理解了单项式的本质就是一个数.学生的已有经验是有关数的运算性质，如交换律、结合律等.所以对于案例5，让学生直接调用已有经验猜想结果,再多方印证也许会更好．数学教学的最终目的就是要教会学生用理性思维思考，当学生已经能理性思考的时候就不要再经历从感性到理性的倒退了.

5.忽视知识内在系统，使上升过程碎片化

学程具有整体性，认知也具有整体性，在数学中有相当一些表面上看毫不相干而本质密切相连的内容.所以，学程前总结要求我们在新知教学时要将新知识置于学生整体的认知结构中进行，以提升学生系统掌握知识的能力.然而在一些课堂中，教师为了所谓的效率，经常不顾知识的系统性，做一些“切头去尾烧中段”的事情，只重视知识的灌输，技能的操练，忽视知识之间的本质联系.

案例6：“平方根（第1课时）”导入部分简述.

教师从加法与减法互为逆运算入手，让学生理解已知和与一个加数求另一个加数的运算是减法，也就是加法的逆运算；再从乘法与除法运算入手，引导学生理解已知积和一个因数求另一个因数的运算是除法，也就是乘法的逆运算；接着提出乘方的逆运算是求什么的运算呢？引导学生得出已知幂和指数求底数或已知幂和底数求指数是乘方的两种逆运算，从而导入课题.

【评析】在本节课的设计中，教师抓住了学生关于互逆运算认知的源头，通过加减对比，乘除对比，揭示出运算的本质是已知两个数求第三个数，进一步揭示“逆”的含义.在此基础上，引导学生对新学运算乘方进行分析，探究乘方的逆运算.从教学实录中可以看到，教师的引入点正是学生的最近发展区，学生在此基础上探索出乘方运算的两种逆运算，并深刻理解了互逆运算，理解了互逆运算的算理，学生的脑子里将不再是孤立计算，而是各种计算内在的联系.当然，有不少教师认为这样做会效率低下.这就要看我们的目的，如果只盯着这一节课的知识，着眼于什么是平方根，如何求平方根，那么教师这样做就让人觉得效率低下；但是，如果教师着眼于乘方与开方关系的深刻理解，着眼于平方根、立方根、四次方根，直至n次方根的运算与算理的理解，那么这节课实际上就是一个长程预设，是一个战略性的布局，短时的低效会换来长久的高效.

6.缺乏长程预设意识，使提升过程自发化

学程前总结是一个催芽的过程，种子发芽是需要一定的条件的.教师的作用在于两点：一是要懂得各种种子发芽所需要的条件；二是要能创设或营造相关的条件．《标准》也指出，数学中有一些重要内容、方法、思想是需要学生经历较长的认识过程，逐步理解和掌握的.因此，在实际教学过程中，教师要重视长程预设，在相关知识再现时，要及时引导学生和前期知识进行对比、总结和提炼，激活生长点，使新知成为原有认知的自然、自主生长，使新知纳入原有的认知结构，使提升变为一种自主、自觉的行为，这就是《标准》所强调的螺旋上升.但是，在实际教学过程中，这种有意识的总结提升还没有受到一线教师的普遍重视，或者说部分一线教师还缺少长程预设的意识和能力，使得提升处于自发状态之中.

例如，在二元一次方程的教学过程中有教师只片面强调未知数的值与等式成立之间的相等关系，而忽视一个未知数随另一个未知数的变化关系，忽视其中的不等关系；在教学不等式时只强调不等式（组）的解法，而忽视不等之中的相等，不等之中的变化；在教学函数相关内容时又只片面强调两个未知数之间的变化关系，而忽视变化关系中存在的相等或不等关系.这样我们的教学过程被人为割裂，方程就是方程，不等式就是不等式，函数就是函数，等学完方程、不等式和函数后再专门研究从函数的角度看方程、从函数的角度看不等式，进行人为的捏合、拼凑，最终形成的知识、经验、方法都是零散的.所以为什么不从一开始学习方程时就做一个长程预设，将方程、不等式和函数都贯穿其中呢？

案例7：方程、不等式、函数的导入设计.

用一根长为40的铁丝围成一个长方形，请你再补充适当的条件，自编一道数学题.

在教师的引导下，学生可能编出以下一些问题：

（1）若长比宽多2，求长；

（2）求长和宽之间的关系；

（3）若长方形的面积为96，求长；

（4）若长方形的面积不小于51，求长的取值范围；

（5）若长方形的面积不大于51，且长为整数，求满足条件的长方形的个数；

（6）求所围成长方形面积的最大值；

……

在提出这些问题之后，教师列出相关的表达式，揭示它们之间的关系，再根据当时教学的需要选择相关表达式切入课题进行研究.

【评析】案例7通过设置一个自编数学题的开放情境，可以将一元一次方程（如问题1）、二元一次方程和一次函数（如问题2）,一元二次方程（如问题3）,二函数与方程、不等式（如问题4，5，6）有机地联系起来，让学生深切体会并理解方程、不等式与函数存在着内在的联系，是一个有机的整体，为主动的、自觉的提升打下坚实的基础.

总之，“学程前总结——将学生引入最近发展区”是一个永恒的教育课题，如何激活学生思维的生长点，让学生永远处于思维发展区的最前沿，除了要避开这些常见的误区外还有更多的课题等待我们去研究，仅以此文抛砖引玉，求教于大家.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］徐小建，李庾南.浅谈中学数学学程总结技艺：兼谈以时间为序的学程总结［J］.中国数学教育（初中版），2013（10）：8-10，18.

［4］蒲大勇.初中数学教学中违背学生认知规律例析［J］.中国数学教育（初中版），2014（10）：40-45，48.

［5］徐小建.都是“出新”惹的祸：例谈我们需要怎样的情境［J］.中学数学杂志（初中版），2010（10）：18-20．

2016—09—01

江苏省“十二五”规划重点资助课题——中学数学学程总结技艺研究（B-a/2013/02/004）.

徐小建（1970—）， 男，中学高级教师，主要从事中学数学教育、教学研究．